|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика]]>>[[Математика 6 клас|Математика 6 клас]]>> Математика: Тема 1.Кратні натурального числа. Найменше спільне кратне''' | + | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика]]>>[[Математика 6 клас|Математика 6 клас]]>>Кратні натурального числа. Найменше спільне кратне''' |
| | | | |
| - | Числа 36, 72, 180 діляться на 18. Кажуть, що числа 36, 72, 180 кратні числу 18.<br>Будь-яке натуральне число, яке ділиться на дане натуральне число, називають кратним даному числу.<br>Усі числа, кратні числу 18, можна одержати, множачи число 18 послідов¬но на числа 1,2,3, 4, 5, ... .<br>18, 36, 54, 72, 90, ... — числа, кратні 18.<br>Кожне натуральне число мас безліч чисел, кратних йому, найменшим з яких є саме це число.<br>Запишіть числа, кратні 9, і числа, кратні 12, та підкресліть їх спільні<br>кратні.<br>число9 кратні: 9.18,27,36,45,54,63,72,81,... число 12 кратні: 12, 24, 36, 48, 60, 72, 84, ...<br>Спільними кратними чисел 9 і 12 е підкреслені числа 36, 72, ... . Усі вони діляться на 9 і на 12. Найменшим спільним кратним є число 36.<br>Найменшим спільним кратним двох натуральних чисел називають найменше натуральне число, яке ділиться на кож¬не з даних чисел.<br>Те, що найменшим спільним кратним чисел 9 і 12с число 36, скорочено записують так: НСК(9; 12) = 36.<br>Розкладемо числа 9, 12 і їх найменше спільне кратне 36 на прості множники:<br>9 = 3-3; 12 = 2-2-3; 36 = 2-2-3-3. Бачимо, що розклад числа 36 можна одержати, коли розклад числа 9 помножити на 2 • 2. Числа 2 і 2 — це такі множники з розкладу числа 12, яких немас в позклалі числа 9.<br>Назвіть послідовність кроків у знаходженні ИСК двох чисел.<br>Щоб знайти найменше спільне кратне двох чисел, можна кожне з них розкласти на прості множники, і розклад одного з чисел помножити на ті множ¬ники іншого числа, яких немас в розкладі першого.<br>Знайдемо найменше спільне кратне чисел 90 і 210.<br>90 = 2•3•3•5; 210 = 2 • 3 • 5 • 7;<br>НСК(90; 210) = 2 • 3 • 3 • 5 • 7 = 630.<br>Якщо одне із чисел ділиться на інше, то більше з них є найменшим спіль¬ним кратним цих чисел. Наприклад, НСК(21; 63) = 63.<br>Найменшим спільним кратним двох взаємно простих чисел є добуток цих чисел. Наприклад, НСК(8; 9) = 72.<br>Найменше спільне кратне можна знайти не тільки для двох, але й для трьох і більше чисел.<br>Наприклад, для чисел 12, 18, 24 маємо:<br>12 = 2•2•3; 18 = 2•3•3; 24 = 2•2•2•3;<br>НСК(12; 18; 24) = 2 • 2 • 3 • 3 • 2 = 72.<br>Прочитайте<br>1. Знайти найменше чотирицифрове число, кратне 27.<br>• 1000 — найменше чотирицифрове число. Поділимо його на 27: 1000 : 27 = 37 (ост. 1).<br>27 • 38 = 1026 — найменше чотирицифрове число, кратне 27. •<br>2. Крок батька дорівнює 72 см, а крок сина — 54 см. Знайти найменшу відстань, яку потрібно пройти як батькові, так і синові, щоб кожен з них зробив при цьому ціле число кроків.<br>• Шукана відстань у сантиметрах повинна виражатись таким найменшим числом, яке ділиться на 72 і на 54. Таким числом є найменше спільне кратне цих чисел. Знайдемо НСК(54; 72):<br>54 = 2•3•3•3; 72 = 2 • 2 • 2 • 3 • 3;<br>НСК(54; 72) = 2• 3• 3• 3• 2• 2 = 216. Отже, шукана відстань дорівнює 216 см. На такій відстані батько зробить 216:72 = 3 кроки, а син — 216:54 = 4 кроки. •<br>3. Знайти найменше спільне кратне чисел 15 і 12.<br>• Знаходимо кратні більшого із чисел і перевіряємо, чи діляться вони на менше число: 15 не ділиться на 12; 15 • 2 = ЗО — не ділиться на 12; 15 • 3 = 45 — не ділиться на 12; 15 • 4 = 60 — ділиться на 12. Отже, НСК(15; 12) = 60. •<br>Усно<br>153. Чи є число 45 спільним кратним чисел 9 і 15; 3 і 18?<br>154. Назвіть кілька спільних кратних чисел 4 і 5; 10 і 15.<br>155. Знайдіть найменше спільне кратне чисел: а) 2 ІЗ; 9 і 18; 20 і 15; 30 і 45;<br>6)2, 3 і 5; 10, 15 і 20; 5, 10 і 15.<br>Рівень А<br>Перевірте, чи буде перше число кратним другому:<br>156. а) 342 і 19; б) 21 324 і 108; в) 9225 і 45.<br>157<br>а) 492 і 41; б) 14 544 і 24; в) 4028 і 212.<br>158. Запишіть числа, менші від 150 і кратні числу 35.<br>159.<br>Запишіть два числа, більші ніж 100 і кратні числу 28.<br>160. Доведіть, що дані числа є взаємно простими, та знайдіть їх найменше спільне кратне:<br>а) 8 і 9; б) 12 і 7; в) 4 і 25.<br>161. Знайдіть найменше спільне кратне чисел т і п, якщо: а) т = 2 • 3• 3 • 5, п = 2 • 3 • 7;<br>б т = 2•2•2•3 • 11, п = 2•2•3•3 • 11.<br>Г162.<br>Знайдіть найменше спільне кратне чисел m, п і к, якщо »1 = 2-3-3-5, « = 3-3-11, к = 2 -2 -2-3 -5.<br>Знайдіть найменше спільне кратне чисел:<br>163. а) 9 і 24; б) 15 і 35; в) 48 і 60; г) 24 і 108;<br>д) 340 і 102; е) 444 і 296; є) 12, 18 і 42; ж) 360, 540 і 640.<br>164.<br>а) 12 і 16; б) 25 і 35; в) 80 і 60; г) 110 і 121;<br>д) 296 і 345; е) 186 і 248; є) 16, 24 і 36; ж) 340, 510 і 680.<br>165. Знайдіть найменше спільне кратне знаменників дробів:<br>[[Image:qm8.jpg]]<br>
| |
| | | | |
| - | Рівень Б<br>166. Знайдіть найбільше трицифрове число, кратне 29.<br>167.<br>Знайдіть найменше чотирицифрове число, кратне 64.<br>168. Автомобіль вантажністю 3 г загрузили ящиками масою по 55 кг. Скільки ящиків загрузили, якщо їх загальна маса більша ніж 2,9 т?<br>169. Скільки є трицифрових чисел, кратних 37? Знайдіть з них ті, запис яких закінчується цифрою 8.<br>170. Скільки є трицифрових чисел, кратних 46? Знайдіть з них ті, запис яких закінчується цифрою 6.<br>471<br>Знайдіть усі трицифрові числа, кратні 43, запис яких закінчується цифрою 5.<br>172. Порівняйте добуток а • b з добутком НСД(а; b) • НСК(а; b), якщо: а = 6, Ь = 8; а= 18,6 = 24.<br>173. Маленька коробка вміщує 12 олівців, а велика — 30. Знайдіть найменшу кількість олівців, які можна запакувати як лише в малі, так і лише у вели¬кі коробки.<br>174:<br>Яке найменше число метрів тканини повинно бузи у сувої, щоб її можна було продати відрізами лише по 3 м або лише по 4 м?<br>175. Рейс автобуса одного маршруту триває 48 хв, а іншого — 56 хв. Уперше ці автобуси одночасно вирушили зі спільної кінцевої зупинки о 6-й годині. О котрій годині вони вдруге одночасно вирушать із цієї зупинки?<br>176<br>Відрізок АВ можна поділити на рівні відрізки завдовжки 42 мм, 63 мм та 84 мм. Яку найменшу довжину може мати відрізок А В"?<br>177. Три теплоходи здійснюють різні туристичні круїзи. Перший круїз триває 12, другий — 9, третій — 18 діб. Повернувшись у порт, теплоходи наступного дня вирушають у новий круїз. 1 травня всі три теплоходи вийшли з порту за своїми маршрутами. Доведіть, що протягом травня всі три теплоходи не зустрінуться в порту одночасно.<br>178. На промені від його початку О послідовно відклали 7 відрізків завдовжки 15 см, а потім знову від точки О — 7 відрізків завдовжки 18 см. Чи мають відрізки завдовжки 15 см і відрізки завдовжки 18 см спільні кінці, відмінні від точки О'?<br>Здогадайтеся<br>179. Якою може бути остання цифра числа, кратного:<br>а) 2; 6)3; в) 561.<br>Вправи для повторення<br>180. Лижник проїхав з гори 3 км 900 м, що становить 65% усього шляху. Знайдіть весь шлях.<br>181. Сума двох чисел дорівнює 14,85, до того ж, перше число на 1,25 більше від другого. Знайдіть ці числа.<br>182. Виконайте дії:<br>[[Image:qm9.jpg]]
| + | Числа 36, 72, 180 діляться на 18. Кажуть, що числа 36, 72, 180 кратні числу 18. |
| | | | |
| - | Пам'ятка до §1<br>1. 24 = 6 • 4; 6 і 4 — дільники числа 24.<br>2. Число 210 ділиться на 10, бо закінчується 0.<br>3. Числа 140 і 135 діляться на 5, бо закінчуються 0 або 5.<br>4. Числа 510, 512, 324, 126, 438 діляться на 2, бо закінчуються одноцифровим парним числом.<br>5. Число 741 ділиться на 3; 7 + 4+1 = 12; 12:3 = 4, сума цифр ділиться на 3. Число 711 ділиться на 9; 7+1 + 1=9; 9:9= 1, сума цифр ділиться на 9.<br>6. Число 17 ділиться лише на 1 і 17; 17 — просте число; дільниками є 1 і саме число.<br>Число 14 ділиться не лише на 1 і 14, а й на 2; 14 — складене число; дільників більше двох.<br>7. НСД( 18; 24) = 6; 6 — найбільше натуральне число, на яке діляться 18 і 24.<br>8. НСК(50: 75) = 150; 150 — найменше натуральне число, яке ділиться на 50 і на 75.<br>Запитання для самоперевірки і повторення<br>1. Яке число називають дільником даного числа? Наведіть приклад.<br>2. Сформулюйте ознаку подільності на 10; на 5; на 2; на 9; на 3.<br>3. Чим відрізняється складене число від простого?<br>4. Які числа називають взаємно простими?<br>5. Що називають найбільшим спільним дільником двох чисел?<br>6. Як знайти найбільший спільний дільник кількох чисел?<br>7. Яке число називають кратним даному числу? Наведіть приклад.<br>8. Що називають найменшим спільним кратним двох чисел?<br>9. Як знайти найменше спільне кратне кількох чисел?<br><br>Завдання для повторення § 1<br><br>183. Знайдіть усі дільники чисел 28; 38; 172.<br>184. Із чисел 117, 181, 195, 288, 600, 1512, 2055, 23 110, 413 775 випишіть ті, що діляться на 2; на 3; на 5; на 9; на 10.<br>185. Поставте замість зірочок такі цифри, щоб число:<br>а) *43* ділилось на 3 і на 10; б) 723** ділилось на 9 і на 10.<br>186. Скільки дільників мають числа 1; 2; 29; 42; 61; 102; 121? Випишіть спо¬чатку прості числа, а потім складені.<br>187. Розкладіть на прості множники числа 22; 32; 51; 126; 400; 7429.<br>188. Чи є взаємно простими числа:<br>а) 15 і 102; б) 42 і 25; в) 101 і 265; г) 1200 і 2401?<br>189. Знайдіть найбільший спільний дільник чисел:<br>а)2 і 28; б) 33 і 132; в)36 і 162;<br>г) 102 і 81; д)4, 6 і 16; е) 42, 70 і 112.<br>190. Знайдіть найменше спільне кратне чисел:<br>а)8 і 24; б) 12 і 52; в) 45 і 105;<br>г) 64 і 96; д) 15, 35 і 45; е) 160, 240 і 400.<br>191. Потрібно розділити на групи 54 шестикласники і 45 п'ятикласників так, щоб в усіх групах була однакова кількість шестикласників і однакова кількість п'ятикласників. Яку найменшу кількість учнів може мати одна така група?<br>192. Якої найменшої довжини повинна бути труба, щоб її можна було розрізати на рівні частини завдовжки 240 см і на рівні частини завдовжки 360 см?<br>193. Учні шостого класу, в якому навчається більше, ніж 20 школярів, купили разом 203 зошити, до того ж, кожен учень купив однакову кількість зошитів. Скільки у класі учнів і скільки зошитів купив кожен учень?<br>194. Яке найменше число одержимо, якщо, ділячи його на 2, отримаємо оста¬чу 1, ділячи на 3 — остачу 2, ділячи на 4 — остачу 3, ділячи на 5 — оста¬чу 4, ділячи на 6 — остачу 5 і воно ділиться на 7?<br>Завдання для самоперевірки<br>І рівень<br>1. Дільником числа 48 є:<br>а) 5; 6)7; в) 12; г) 18.<br>2. На 5 ділиться число:<br>а) 552; 6)150; в) 541; г) 359.<br>3. На 9 ділиться число:<br>а) 119; 6)189; в) 971; г)475.<br>4. Спільним дільником чисел 42 і 63 є:<br>а) 27; 6)9; в) 6; г) 7.<br>5. Найбільшим спільним дільником чисел 42 і 63 є:<br>а) 9; 6)7; в) 21; г) 3.<br>6. Найменшим спільним кратним чисел 28 і 35 є:<br>а) 70; 6)140; в) 175; г) 280.<br>II рівень<br>7. Знайдіть найбільший спільний дільник чисел 28 і 42.<br>8. Знайдіть найменше спільне кратне чисел 35 і 56.<br>9. Поставте замість зірочок такі цифри, щоб число 532** ділилося на 2 і на 3.<br>/// рівень<br>10. Чи є взаємно простими числа 245 і 500; 17 і 355; 111 і 252?<br>11. Використовуючи цифри 0, 2, 3, 7, 8 не більше одного разу, запишіть чоти¬рицифрове число, яке ділилося б на 3 і на 5.<br>12. Якої найменшої довжини повинна бути дошка, щоб її можна було розрі¬зати без залишків на рівні частини завдовжки як 72 см, так і 96 см?<br>IV рівень<br>13. Запишіть усі правильні дроби зі знаменником 16, у яких чисельник і знаменник — взаємно прості числа.<br>14. Замініть зірочку такою цифрою та знайдіть таке число а, щоб була правильною рівність 280* = 3 •5 • 11 • а.<br>15. У магазині є ножі та виделки загальною кількістю від 320 до 400 штук. Якщо їх рахувати десятками, то буде ціле число десятків, якщо рахувати дюжинами (по 12), то буде ціле число дюжин. Скільки в магазині виделок і скільки ножів, якщо ножів на 160 менше, ніж виделок?<br>
| + | <br>Будь-яке натуральне число, яке ділиться на дане натуральне число, називають кратним даному числу. |
| | | | |
| - | <br> <sub>[[Гіпермаркет Знань - перший в світі!|Онлайн-бібліотека з підручниками]] і книгами, тести [[Математика|з математики]], завдання [[Математика 6 клас|з математики 6 клас]], календарне планування</sub> | + | <br>Усі числа, кратні числу 18, можна одержати, множачи число 18 послідовно на числа 1,2,3, 4, 5, ... .<br>18, 36, 54, 72, 90, ... — числа, кратні 18. |
| | | | |
| - | <br> Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту<br> | + | <br>Кожне натуральне число мас безліч чисел, кратних йому, найменшим з яких є саме це число. |
| | | | |
| - | [[Image:1236084776 kr.jpg|10x10px]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B2%D0%B8%D1%87%D0%B0%D0%B9%D0%BD%D0%B8%D1%85_%D0%B4%D1%80%D0%BE%D0%B1%D1%96%D0%B2._%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D1%83_%D1%96_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%B8%D0%B9_%D0%BA%D0%B0%D1%80%D0%BA%D0%B0%D1%81 конспект уроку і опорний каркас] | + | <br>Запишіть числа, кратні 9, і числа, кратні 12, та підкресліть їх спільні кратні.<br>число9 кратні: 9.18,27,36,45,54,63,72,81,... число 12 кратні: 12, 24, 36, 48, 60, 72, 84, ...<br>Спільними кратними чисел 9 і 12 є підкреслені числа 36, 72, ... . Усі вони діляться на 9 і на 12. Найменшим спільним кратним є число 36. |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентація уроку | + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративні методи та інтерактивні технології | + | <br>Найменшим спільним кратним двох натуральних чисел називають найменше натуральне число, яке ділиться на кожне з даних чисел. |
| - | [[Image:1236084776 kr.jpg|10x10px]] закриті вправи (тільки для використання вчителями) | + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] оцінювання | + | <br>Те, що найменшим спільним кратним чисел 9 і 12с число 36, скорочено записують так: НСК(9; 12) = 36. |
| | + | |
| | + | <br>Розкладемо числа 9, 12 і їх найменше спільне кратне 36 на прості множники:<br>9 = 3-3; 12 = 2-2-3; 36 = 2-2-3-3. Бачимо, що розклад числа 36 можна одержати, коли розклад числа 9 помножити на 2 • 2. Числа 2 і 2 — це такі множники з розкладу числа 12, яких немас в позклалі числа 9. |
| | + | |
| | + | <br>Назвіть [[Акселеративні_методи_до_уроку:_Склад_числа_10._Послідовність_чисел_у_межах_10._Порівняння_чисел|послідовність]] кроків у знаходженні ИСК двох чисел. |
| | + | |
| | + | <br>Щоб знайти найменше спільне кратне двох чисел, можна кожне з них розкласти на прості множники, і розклад одного з чисел помножити на ті множники іншого числа, яких немас в розкладі першого. |
| | + | |
| | + | <br>Знайдемо найменше спільне кратне чисел 90 і 210.<br>90 = 2•3•3•5; 210 = 2 • 3 • 5 • 7;<br>НСК(90; 210) = 2 • 3 • 3 • 5 • 7 = 630. |
| | + | |
| | + | <br>Якщо одне із чисел ділиться на інше, то більше з них є найменшим спільним [[Наименьшее_общее_кратное|кратним]] цих чисел. Наприклад, НСК(21; 63) = 63. |
| | + | |
| | + | <br>Найменшим спільним кратним двох взаємно простих чисел є добуток цих чисел. Наприклад, НСК(8; 9) = 72.<br>Найменше спільне кратне можна знайти не тільки для двох, але й для трьох і більше чисел. |
| | + | |
| | + | <br>Наприклад, для чисел 12, 18, 24 маємо:<br>12 = 2•2•3; 18 = 2•3•3; 24 = 2•2•2•3;<br>НСК(12; 18; 24) = 2 • 2 • 3 • 3 • 2 = 72. |
| | + | |
| | + | <br>'''Прочитайте'''<br>1. Знайти найменше чотирицифрове число, кратне 27.<br>• 1000 — найменше чотирицифрове число. Поділимо його на 27: 1000 : 27 = 37 (ост. 1).<br>27 • 38 = 1026 — найменше чотирицифрове число, кратне 27. |
| | + | |
| | + | <br>2. Крок батька дорівнює 72 см, а крок сина — 54 см. Знайти найменшу відстань, яку потрібно пройти як батькові, так і синові, щоб кожен з них зробив при цьому ціле число кроків.<br> |
| | + | |
| | + | Шукана відстань у сантиметрах повинна виражатись таким найменшим числом, яке ділиться на 72 і на 54. Таким числом є найменше спільне кратне цих чисел. Знайдемо НСК(54; 72):<br>54 = 2•3•3•3; 72 = 2 • 2 • 2 • 3 • 3;<br>НСК(54; 72) = 2• 3• 3• 3• 2• 2 = 216. Отже, шукана відстань дорівнює 216 см. На такій відстані батько зробить 216:72 = 3 кроки, а син — 216:54 = 4 кроки. |
| | + | |
| | + | <br>3. Знайти найменше спільне [[Кратне_порівняння_чисел|кратне]] чисел 15 і 12.<br>• Знаходимо кратні більшого із чисел і перевіряємо, чи діляться вони на менше число: 15 не ділиться на 12; 15 • 2 = 30 — не ділиться на 12; 15 • 3 = 45 — не ділиться на 12; 15 • 4 = 60 — ділиться на 12. Отже, НСК(15; 12) = 60. |
| | + | |
| | + | <br>'''Усно'''<br>153. Чи є число 45 спільним кратним чисел 9 і 15; 3 і 18? |
| | + | |
| | + | <br>154. Назвіть кілька спільних кратних чисел 4 і 5; 10 і 15. |
| | + | |
| | + | <br>155. Знайдіть найменше спільне кратне чисел: а) 2 ІЗ; 9 і 18; 20 і 15; 30 і 45;<br>6)2, 3 і 5; 10, 15 і 20; 5, 10 і 15. |
| | + | |
| | + | <br>'''Рівень А'''<br>Перевірте, чи буде перше число кратним другому:<br>156. а) 342 і 19; б) 21 324 і 108; в) 9225 і 45. |
| | + | |
| | + | <br>157. а) 492 і 41; б) 14 544 і 24; в) 4028 і 212. |
| | + | |
| | + | <br>158. Запишіть числа, менші від 150 і кратні числу 35. |
| | + | |
| | + | <br>159. Запишіть два числа, більші ніж 100 і кратні числу 28. |
| | + | |
| | + | <br>160. Доведіть, що дані числа є взаємно простими, та знайдіть їх найменше спільне кратне:<br>а) 8 і 9; б) 12 і 7; в) 4 і 25. |
| | + | |
| | + | <br>161. Знайдіть найменше спільне кратне чисел т і п, якщо: а) т = 2 • 3• 3 • 5, п = 2 • 3 • 7;<br>б т = 2•2•2•3 • 11, п = 2•2•3•3 • 11. |
| | + | |
| | + | <br>162. Знайдіть найменше спільне кратне чисел m, п і к, якщо »1 = 2-3-3-5, « = 3-3-11, к = 2 -2 -2-3 -5. |
| | + | |
| | + | <br>Знайдіть найменше спільне кратне чисел:<br>163. а) 9 і 24; б) 15 і 35; в) 48 і 60; г) 24 і 108;<br>д) 340 і 102; е) 444 і 296; є) 12, 18 і 42; ж) 360, 540 і 640. |
| | + | |
| | + | <br>164. а) 12 і 16; б) 25 і 35; в) 80 і 60; г) 110 і 121;<br>д) 296 і 345; е) 186 і 248; є) 16, 24 і 36; ж) 340, 510 і 680. |
| | + | |
| | + | <br>165. Знайдіть найменше спільне кратне знаменників дробів:<br>[[Image:Qm8.jpg|400px|найменше спільне кратне]]<br> |
| | + | |
| | + | |
| | + | |
| | + | '''Рівень Б'''<br>166. Знайдіть найбільше трицифрове число, кратне 29. |
| | + | |
| | + | <br>167. Знайдіть найменше чотирицифрове число, кратне 64. |
| | + | |
| | + | <br>168. Автомобіль вантажністю 3 г загрузили ящиками масою по 55 кг. Скільки ящиків загрузили, якщо їх загальна маса більша ніж 2,9 т? |
| | + | |
| | + | <br>169. Скільки є [[Ділення_трицифрових_чисел_на_двоцифрові|трицифрових чисел]], кратних 37? Знайдіть з них ті, запис яких закінчується цифрою 8. |
| | + | |
| | + | <br>170. Скільки є трицифрових чисел, кратних 46? Знайдіть з них ті, запис яких закінчується цифрою 6.<br>471<br>Знайдіть усі трицифрові числа, кратні 43, запис яких закінчується цифрою 5.<br>172. Порівняйте добуток а • b з добутком НСД(а; b) • НСК(а; b), якщо: а = 6, Ь = 8; а= 18,6 = 24. |
| | + | |
| | + | <br>173. Маленька коробка вміщує 12 олівців, а велика — 30. Знайдіть найменшу кількість олівців, які можна запакувати як лише в малі, так і лише у великі коробки. |
| | + | |
| | + | <br>174. Яке найменше число метрів тканини повинно бузи у сувої, щоб її можна було продати відрізами лише по 3 м або лише по 4 м? |
| | + | |
| | + | <br>175. Рейс автобуса одного маршруту триває 48 хв, а іншого — 56 хв. Уперше ці автобуси одночасно вирушили зі спільної кінцевої зупинки о 6-й годині. О котрій годині вони вдруге одночасно вирушать із цієї зупинки? |
| | + | |
| | + | <br>176. [[Точка,_пряма,_площина._Промінь._Відрізок|Відрізок]] АВ можна поділити на рівні відрізки завдовжки 42 мм, 63 мм та 84 мм. Яку найменшу довжину може мати відрізок А В"? |
| | + | |
| | + | <br>177. Три теплоходи здійснюють різні [[Презентація_2_до_теми_"Туристичні_послуги"|турист]]ичні круїзи. Перший круїз триває 12, другий — 9, третій — 18 діб. Повернувшись у порт, теплоходи наступного дня вирушають у новий круїз. 1 травня всі три теплоходи вийшли з порту за своїми маршрутами. Доведіть, що протягом травня всі три теплоходи не зустрінуться в порту одночасно. |
| | + | |
| | + | <br>178. На промені від його початку О послідовно відклали 7 відрізків завдовжки 15 см, а потім знову від точки О — 7 відрізків завдовжки 18 см. Чи мають відрізки завдовжки 15 см і відрізки завдовжки 18 см спільні кінці, відмінні від точки О? |
| | + | |
| | + | <br>'''Здогадайтеся'''<br>179. Якою може бути остання цифра числа, кратного:<br>а) 2; б)3; в) 561. |
| | + | |
| | + | <br>'''Вправи для повторення'''<br>180. Лижник проїхав з гори 3 км 900 м, що становить 65% усього шляху. Знайдіть весь шлях. |
| | + | |
| | + | <br>181. Сума двох чисел дорівнює 14,85, до того ж, перше число на 1,25 більше від другого. Знайдіть ці числа. |
| | + | |
| | + | <br>182. Виконайте дії:<br>[[Image:Qm9.jpg|400px|Виконайте дії]] |
| | + | |
| | + | |
| | + | |
| | + | '''Пам'ятка до §1''' |
| | + | |
| | + | <br>1. 24 = 6 • 4; 6 і 4 — дільники числа 24. |
| | + | |
| | + | <br>2. Число 210 ділиться на 10, бо закінчується 0. |
| | + | |
| | + | <br>3. Числа 140 і 135 діляться на 5, бо закінчуються 0 або 5. |
| | + | |
| | + | <br>4. Числа 510, 512, 324, 126, 438 діляться на 2, бо закінчуються одноцифровим парним числом. |
| | + | |
| | + | <br>5. Число 741 ділиться на 3; 7 + 4+1 = 12; 12:3 = 4, сума цифр ділиться на 3. Число 711 ділиться на 9; 7+1 + 1=9; 9:9= 1, сума цифр ділиться на 9. |
| | + | |
| | + | <br>6. Число 17 ділиться лише на 1 і 17; 17 — просте число; дільниками є 1 і саме число.<br>Число 14 ділиться не лише на 1 і 14, а й на 2; 14 — складене число; дільників більше двох. |
| | + | |
| | + | <br>7. НСД( 18; 24) = 6; 6 — найбільше натуральне число, на яке діляться 18 і 24. |
| | + | |
| | + | <br>8. НСК(50: 75) = 150; 150 — найменше [[Задачі_до_теми_Ділення_десяткових_дробів_на_натуральне_число_Самостійна_робота|натуральне число]], яке ділиться на 50 і на 75. |
| | + | |
| | + | <br>'''Запитання для самоперевірки і повторення'''<br>''1. Яке число називають дільником даного числа? Наведіть приклад.<br>2. Сформулюйте ознаку подільності на 10; на 5; на 2; на 9; на 3.<br>3. Чим відрізняється складене число від простого?<br>4. Які числа називають взаємно простими?<br>5. Що називають найбільшим спільним дільником двох чисел?<br>6. Як знайти найбільший спільний дільник кількох чисел?<br>7. Яке число називають кратним даному числу? Наведіть приклад.<br>8. Що називають найменшим спільним кратним двох чисел?<br>9. Як знайти найменше спільне кратне кількох чисел?''<br><br>'''Завдання для повторення § 1'''<br><br>183. Знайдіть усі [[Найбільший_спільний_дільник|дільник]]и чисел 28; 38; 172. |
| | + | |
| | + | <br>184. Із чисел 117, 181, 195, 288, 600, 1512, 2055, 23 110, 413 775 випишіть ті, що діляться на 2; на 3; на 5; на 9; на 10. |
| | + | |
| | + | <br>185. Поставте замість зірочок такі цифри, щоб число:<br>а) *43* ділилось на 3 і на 10; б) 723** ділилось на 9 і на 10. |
| | + | |
| | + | <br>186. Скільки дільників мають числа 1; 2; 29; 42; 61; 102; 121? Випишіть спочатку прості числа, а потім складені. |
| | + | |
| | + | <br>187. Розкладіть на прості множники числа 22; 32; 51; 126; 400; 7429. |
| | + | |
| | + | <br>188. Чи є взаємно простими числа:<br>а) 15 і 102; б) 42 і 25; в) 101 і 265; г) 1200 і 2401? |
| | + | |
| | + | <br>189. Знайдіть найбільший спільний дільник чисел:<br>а)2 і 28; б) 33 і 132; в)36 і 162;<br>г) 102 і 81; д)4, 6 і 16; е) 42, 70 і 112. |
| | + | |
| | + | <br>190. Знайдіть найменше спільне кратне чисел:<br>а)8 і 24; б) 12 і 52; в) 45 і 105;<br>г) 64 і 96; д) 15, 35 і 45; е) 160, 240 і 400. |
| | + | |
| | + | <br>191. Потрібно розділити на групи 54 шестикласники і 45 [[5_клас_уроки|п'ятикласник]]ів так, щоб в усіх групах була однакова кількість шестикласників і однакова кількість п'ятикласників. Яку найменшу кількість учнів може мати одна така група? |
| | + | |
| | + | <br>192. Якої найменшої довжини повинна бути труба, щоб її можна було розрізати на рівні частини завдовжки 240 см і на рівні частини завдовжки 360 см? |
| | + | |
| | + | <br>193. Учні шостого класу, в якому навчається більше, ніж 20 школярів, купили разом 203 зошити, до того ж, кожен учень купив однакову кількість зошитів. Скільки у класі учнів і скільки зошитів купив кожен учень? |
| | + | |
| | + | <br>194. Яке найменше число одержимо, якщо, ділячи його на 2, отримаємо остачу 1, ділячи на 3 — остачу 2, ділячи на 4 — остачу 3, ділячи на 5 — остачу 4, ділячи на 6 — остачу 5 і воно ділиться на 7? |
| | + | |
| | + | <br>'''Завдання для самоперевірки'''<br>І рівень<br>1. Дільником числа 48 є:<br>а) 5; 6)7; в) 12; г) 18.<br>2. На 5 ділиться число:<br>а) 552; 6)150; в) 541; г) 359.<br>3. На 9 ділиться число:<br>а) 119; 6)189; в) 971; г)475.<br>4. Спільним дільником чисел 42 і 63 є:<br>а) 27; 6)9; в) 6; г) 7.<br>5. Найбільшим спільним дільником чисел 42 і 63 є:<br>а) 9; 6)7; в) 21; г) 3.<br>6. Найменшим спільним кратним чисел 28 і 35 є:<br>а) 70; 6)140; в) 175; г) 280. |
| | + | |
| | + | <br>II рівень<br>7. Знайдіть найбільший спільний дільник чисел 28 і 42.<br>8. Знайдіть найменше спільне кратне чисел 35 і 56.<br>9. Поставте замість зірочок такі цифри, щоб число 532** ділилося на 2 і на 3. |
| | + | |
| | + | <br>ІІІрівень<br>10. Чи є взаємно простими числа 245 і 500; 17 і 355; 111 і 252?<br>11. Використовуючи цифри 0, 2, 3, 7, 8 не більше одного разу, запишіть чотирицифрове число, яке ділилося б на 3 і на 5.<br>12. Якої найменшої [[Дифракційна_градка._Вимірювання_довжини_світлової_хвилі_за_допомогою_дифракційної_градки|довжини]] повинна бути дошка, щоб її можна було розрізати без залишків на рівні частини завдовжки як 72 см, так і 96 см? |
| | + | |
| | + | <br>IV рівень<br>13. Запишіть усі правильні дроби зі знаменником 16, у яких чисельник і знаменник — взаємно прості числа.<br>14. Замініть зірочку такою цифрою та знайдіть таке число а, щоб була правильною рівність 280* = 3 •5 • 11 • а.<br>15. У магазині є ножі та виделки загальною кількістю від 320 до 400 штук. Якщо їх рахувати десятками, то буде ціле число десятків, якщо рахувати дюжинами (по 12), то буде ціле число дюжин. Скільки в магазині виделок і скільки ножів, якщо ножів на 160 менше, ніж виделок?<br> |
| | + | |
| | + | |
| | + | |
| | + | ''Математика [[6_клас_уроки|6 клас]] Галина Янченко, Василь Кравчук '' |
| | + | |
| | + | ''Вислано читачами iнтернет-сайту'' |
| | + | |
| | + | <br> <sub>[[Гіпермаркет Знань - перший в світі!|Онлайн-бібліотека з підручниками]] і книгами, тести [[Математика|з математики]], завдання [[Математика 6 клас|з математики 6 клас]], календарне планування</sub><br> |
| | + | |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B2%D0%B8%D1%87%D0%B0%D0%B9%D0%BD%D0%B8%D1%85_%D0%B4%D1%80%D0%BE%D0%B1%D1%96%D0%B2._%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D1%83_%D1%96_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%B8%D0%B9_%D0%BA%D0%B0%D1%80%D0%BA%D0%B0%D1%81 конспект уроку і опорний каркас] |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентація уроку |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративні методи та інтерактивні технології |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] закриті вправи (тільки для використання вчителями) |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] оцінювання |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачі та вправи,самоперевірка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачі та вправи,самоперевірка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикуми, лабораторні, кейси | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикуми, лабораторні, кейси |
| - | [[Image:1236084776 kr.jpg|10x10px]] рівень складності задач: звичайний, високий, олімпійський | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рівень складності задач: звичайний, високий, олімпійський |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашнє завдання | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашнє завдання |
| | | | |
| | '''<u>Ілюстрації</u>''' | | '''<u>Ілюстрації</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа |
| - | [[Image:1236084776 kr.jpg|10x10px]] реферати | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] реферати |
| - | [[Image:1236084776 kr.jpg|10x10px]] фішки для допитливих | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фішки для допитливих |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] гумор, притчі, приколи, приказки, кросворди, цитати | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] гумор, притчі, приколи, приказки, кросворди, цитати |
| | | | |
| | '''<u>Доповнення</u>''' | | '''<u>Доповнення</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] зовнішнє незалежне тестування (ЗНТ) | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] зовнішнє незалежне тестування (ЗНТ) |
| - | [[Image:1236084776 kr.jpg|10x10px]] підручники основні і допоміжні | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] підручники основні і допоміжні |
| - | [[Image:1236084776 kr.jpg|10x10px]] тематичні свята, девізи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] тематичні свята, девізи |
| - | [[Image:1236084776 kr.jpg|10x10px]] статті | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статті |
| - | [[Image:1236084776 kr.jpg|10x10px]] національні особливості | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] національні особливості |
| - | [[Image:1236084776 kr.jpg|10x10px]] словник термінів | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словник термінів |
| - | [[Image:1236084776 kr.jpg|10x10px]] інше | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] інше |
| | | | |
| | '''<u>Тільки для вчителів</u>''' | | '''<u>Тільки для вчителів</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] [http://xvatit.com/Idealny_urok.html ідеальні уроки] | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://xvatit.com/Idealny_urok.html ідеальні уроки] |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарний план на рік | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарний план на рік |
| - | [[Image:1236084776 kr.jpg|10x10px]] методичні рекомендації | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методичні рекомендації |
| - | [[Image:1236084776 kr.jpg|10x10px]] програми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] програми |
| - | [[Image:1236084776 kr.jpg|10x10px]] [http://xvatit.com/forum/ обговорення] | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://xvatit.com/forum/ обговорення] |
| | | | |
| | | | |
Текущая версия на 13:32, 31 октября 2012
Гіпермаркет Знань>>Математика>>Математика 6 клас>>Кратні натурального числа. Найменше спільне кратне
Числа 36, 72, 180 діляться на 18. Кажуть, що числа 36, 72, 180 кратні числу 18.
Будь-яке натуральне число, яке ділиться на дане натуральне число, називають кратним даному числу.
Усі числа, кратні числу 18, можна одержати, множачи число 18 послідовно на числа 1,2,3, 4, 5, ... .
18, 36, 54, 72, 90, ... — числа, кратні 18.
Кожне натуральне число мас безліч чисел, кратних йому, найменшим з яких є саме це число.
Запишіть числа, кратні 9, і числа, кратні 12, та підкресліть їх спільні кратні.
число9 кратні: 9.18,27,36,45,54,63,72,81,... число 12 кратні: 12, 24, 36, 48, 60, 72, 84, ...
Спільними кратними чисел 9 і 12 є підкреслені числа 36, 72, ... . Усі вони діляться на 9 і на 12. Найменшим спільним кратним є число 36.
Найменшим спільним кратним двох натуральних чисел називають найменше натуральне число, яке ділиться на кожне з даних чисел.
Те, що найменшим спільним кратним чисел 9 і 12с число 36, скорочено записують так: НСК(9; 12) = 36.
Розкладемо числа 9, 12 і їх найменше спільне кратне 36 на прості множники:
9 = 3-3; 12 = 2-2-3; 36 = 2-2-3-3. Бачимо, що розклад числа 36 можна одержати, коли розклад числа 9 помножити на 2 • 2. Числа 2 і 2 — це такі множники з розкладу числа 12, яких немас в позклалі числа 9.
Назвіть послідовність кроків у знаходженні ИСК двох чисел.
Щоб знайти найменше спільне кратне двох чисел, можна кожне з них розкласти на прості множники, і розклад одного з чисел помножити на ті множники іншого числа, яких немас в розкладі першого.
Знайдемо найменше спільне кратне чисел 90 і 210.
90 = 2•3•3•5; 210 = 2 • 3 • 5 • 7;
НСК(90; 210) = 2 • 3 • 3 • 5 • 7 = 630.
Якщо одне із чисел ділиться на інше, то більше з них є найменшим спільним кратним цих чисел. Наприклад, НСК(21; 63) = 63.
Найменшим спільним кратним двох взаємно простих чисел є добуток цих чисел. Наприклад, НСК(8; 9) = 72.
Найменше спільне кратне можна знайти не тільки для двох, але й для трьох і більше чисел.
Наприклад, для чисел 12, 18, 24 маємо:
12 = 2•2•3; 18 = 2•3•3; 24 = 2•2•2•3;
НСК(12; 18; 24) = 2 • 2 • 3 • 3 • 2 = 72.
Прочитайте
1. Знайти найменше чотирицифрове число, кратне 27.
• 1000 — найменше чотирицифрове число. Поділимо його на 27: 1000 : 27 = 37 (ост. 1).
27 • 38 = 1026 — найменше чотирицифрове число, кратне 27.
2. Крок батька дорівнює 72 см, а крок сина — 54 см. Знайти найменшу відстань, яку потрібно пройти як батькові, так і синові, щоб кожен з них зробив при цьому ціле число кроків.
Шукана відстань у сантиметрах повинна виражатись таким найменшим числом, яке ділиться на 72 і на 54. Таким числом є найменше спільне кратне цих чисел. Знайдемо НСК(54; 72):
54 = 2•3•3•3; 72 = 2 • 2 • 2 • 3 • 3;
НСК(54; 72) = 2• 3• 3• 3• 2• 2 = 216. Отже, шукана відстань дорівнює 216 см. На такій відстані батько зробить 216:72 = 3 кроки, а син — 216:54 = 4 кроки.
3. Знайти найменше спільне кратне чисел 15 і 12.
• Знаходимо кратні більшого із чисел і перевіряємо, чи діляться вони на менше число: 15 не ділиться на 12; 15 • 2 = 30 — не ділиться на 12; 15 • 3 = 45 — не ділиться на 12; 15 • 4 = 60 — ділиться на 12. Отже, НСК(15; 12) = 60.
Усно
153. Чи є число 45 спільним кратним чисел 9 і 15; 3 і 18?
154. Назвіть кілька спільних кратних чисел 4 і 5; 10 і 15.
155. Знайдіть найменше спільне кратне чисел: а) 2 ІЗ; 9 і 18; 20 і 15; 30 і 45;
6)2, 3 і 5; 10, 15 і 20; 5, 10 і 15.
Рівень А
Перевірте, чи буде перше число кратним другому:
156. а) 342 і 19; б) 21 324 і 108; в) 9225 і 45.
157. а) 492 і 41; б) 14 544 і 24; в) 4028 і 212.
158. Запишіть числа, менші від 150 і кратні числу 35.
159. Запишіть два числа, більші ніж 100 і кратні числу 28.
160. Доведіть, що дані числа є взаємно простими, та знайдіть їх найменше спільне кратне:
а) 8 і 9; б) 12 і 7; в) 4 і 25.
161. Знайдіть найменше спільне кратне чисел т і п, якщо: а) т = 2 • 3• 3 • 5, п = 2 • 3 • 7;
б т = 2•2•2•3 • 11, п = 2•2•3•3 • 11.
162. Знайдіть найменше спільне кратне чисел m, п і к, якщо »1 = 2-3-3-5, « = 3-3-11, к = 2 -2 -2-3 -5.
Знайдіть найменше спільне кратне чисел:
163. а) 9 і 24; б) 15 і 35; в) 48 і 60; г) 24 і 108;
д) 340 і 102; е) 444 і 296; є) 12, 18 і 42; ж) 360, 540 і 640.
164. а) 12 і 16; б) 25 і 35; в) 80 і 60; г) 110 і 121;
д) 296 і 345; е) 186 і 248; є) 16, 24 і 36; ж) 340, 510 і 680.
165. Знайдіть найменше спільне кратне знаменників дробів:
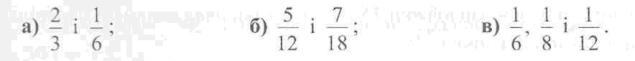
Рівень Б
166. Знайдіть найбільше трицифрове число, кратне 29.
167. Знайдіть найменше чотирицифрове число, кратне 64.
168. Автомобіль вантажністю 3 г загрузили ящиками масою по 55 кг. Скільки ящиків загрузили, якщо їх загальна маса більша ніж 2,9 т?
169. Скільки є трицифрових чисел, кратних 37? Знайдіть з них ті, запис яких закінчується цифрою 8.
170. Скільки є трицифрових чисел, кратних 46? Знайдіть з них ті, запис яких закінчується цифрою 6.
471
Знайдіть усі трицифрові числа, кратні 43, запис яких закінчується цифрою 5.
172. Порівняйте добуток а • b з добутком НСД(а; b) • НСК(а; b), якщо: а = 6, Ь = 8; а= 18,6 = 24.
173. Маленька коробка вміщує 12 олівців, а велика — 30. Знайдіть найменшу кількість олівців, які можна запакувати як лише в малі, так і лише у великі коробки.
174. Яке найменше число метрів тканини повинно бузи у сувої, щоб її можна було продати відрізами лише по 3 м або лише по 4 м?
175. Рейс автобуса одного маршруту триває 48 хв, а іншого — 56 хв. Уперше ці автобуси одночасно вирушили зі спільної кінцевої зупинки о 6-й годині. О котрій годині вони вдруге одночасно вирушать із цієї зупинки?
176. Відрізок АВ можна поділити на рівні відрізки завдовжки 42 мм, 63 мм та 84 мм. Яку найменшу довжину може мати відрізок А В"?
177. Три теплоходи здійснюють різні туристичні круїзи. Перший круїз триває 12, другий — 9, третій — 18 діб. Повернувшись у порт, теплоходи наступного дня вирушають у новий круїз. 1 травня всі три теплоходи вийшли з порту за своїми маршрутами. Доведіть, що протягом травня всі три теплоходи не зустрінуться в порту одночасно.
178. На промені від його початку О послідовно відклали 7 відрізків завдовжки 15 см, а потім знову від точки О — 7 відрізків завдовжки 18 см. Чи мають відрізки завдовжки 15 см і відрізки завдовжки 18 см спільні кінці, відмінні від точки О?
Здогадайтеся
179. Якою може бути остання цифра числа, кратного:
а) 2; б)3; в) 561.
Вправи для повторення
180. Лижник проїхав з гори 3 км 900 м, що становить 65% усього шляху. Знайдіть весь шлях.
181. Сума двох чисел дорівнює 14,85, до того ж, перше число на 1,25 більше від другого. Знайдіть ці числа.
182. Виконайте дії:
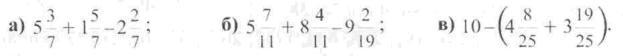
Пам'ятка до §1
1. 24 = 6 • 4; 6 і 4 — дільники числа 24.
2. Число 210 ділиться на 10, бо закінчується 0.
3. Числа 140 і 135 діляться на 5, бо закінчуються 0 або 5.
4. Числа 510, 512, 324, 126, 438 діляться на 2, бо закінчуються одноцифровим парним числом.
5. Число 741 ділиться на 3; 7 + 4+1 = 12; 12:3 = 4, сума цифр ділиться на 3. Число 711 ділиться на 9; 7+1 + 1=9; 9:9= 1, сума цифр ділиться на 9.
6. Число 17 ділиться лише на 1 і 17; 17 — просте число; дільниками є 1 і саме число.
Число 14 ділиться не лише на 1 і 14, а й на 2; 14 — складене число; дільників більше двох.
7. НСД( 18; 24) = 6; 6 — найбільше натуральне число, на яке діляться 18 і 24.
8. НСК(50: 75) = 150; 150 — найменше натуральне число, яке ділиться на 50 і на 75.
Запитання для самоперевірки і повторення
1. Яке число називають дільником даного числа? Наведіть приклад.
2. Сформулюйте ознаку подільності на 10; на 5; на 2; на 9; на 3.
3. Чим відрізняється складене число від простого?
4. Які числа називають взаємно простими?
5. Що називають найбільшим спільним дільником двох чисел?
6. Як знайти найбільший спільний дільник кількох чисел?
7. Яке число називають кратним даному числу? Наведіть приклад.
8. Що називають найменшим спільним кратним двох чисел?
9. Як знайти найменше спільне кратне кількох чисел?
Завдання для повторення § 1
183. Знайдіть усі дільники чисел 28; 38; 172.
184. Із чисел 117, 181, 195, 288, 600, 1512, 2055, 23 110, 413 775 випишіть ті, що діляться на 2; на 3; на 5; на 9; на 10.
185. Поставте замість зірочок такі цифри, щоб число:
а) *43* ділилось на 3 і на 10; б) 723** ділилось на 9 і на 10.
186. Скільки дільників мають числа 1; 2; 29; 42; 61; 102; 121? Випишіть спочатку прості числа, а потім складені.
187. Розкладіть на прості множники числа 22; 32; 51; 126; 400; 7429.
188. Чи є взаємно простими числа:
а) 15 і 102; б) 42 і 25; в) 101 і 265; г) 1200 і 2401?
189. Знайдіть найбільший спільний дільник чисел:
а)2 і 28; б) 33 і 132; в)36 і 162;
г) 102 і 81; д)4, 6 і 16; е) 42, 70 і 112.
190. Знайдіть найменше спільне кратне чисел:
а)8 і 24; б) 12 і 52; в) 45 і 105;
г) 64 і 96; д) 15, 35 і 45; е) 160, 240 і 400.
191. Потрібно розділити на групи 54 шестикласники і 45 п'ятикласників так, щоб в усіх групах була однакова кількість шестикласників і однакова кількість п'ятикласників. Яку найменшу кількість учнів може мати одна така група?
192. Якої найменшої довжини повинна бути труба, щоб її можна було розрізати на рівні частини завдовжки 240 см і на рівні частини завдовжки 360 см?
193. Учні шостого класу, в якому навчається більше, ніж 20 школярів, купили разом 203 зошити, до того ж, кожен учень купив однакову кількість зошитів. Скільки у класі учнів і скільки зошитів купив кожен учень?
194. Яке найменше число одержимо, якщо, ділячи його на 2, отримаємо остачу 1, ділячи на 3 — остачу 2, ділячи на 4 — остачу 3, ділячи на 5 — остачу 4, ділячи на 6 — остачу 5 і воно ділиться на 7?
Завдання для самоперевірки
І рівень
1. Дільником числа 48 є:
а) 5; 6)7; в) 12; г) 18.
2. На 5 ділиться число:
а) 552; 6)150; в) 541; г) 359.
3. На 9 ділиться число:
а) 119; 6)189; в) 971; г)475.
4. Спільним дільником чисел 42 і 63 є:
а) 27; 6)9; в) 6; г) 7.
5. Найбільшим спільним дільником чисел 42 і 63 є:
а) 9; 6)7; в) 21; г) 3.
6. Найменшим спільним кратним чисел 28 і 35 є:
а) 70; 6)140; в) 175; г) 280.
II рівень
7. Знайдіть найбільший спільний дільник чисел 28 і 42.
8. Знайдіть найменше спільне кратне чисел 35 і 56.
9. Поставте замість зірочок такі цифри, щоб число 532** ділилося на 2 і на 3.
ІІІрівень
10. Чи є взаємно простими числа 245 і 500; 17 і 355; 111 і 252?
11. Використовуючи цифри 0, 2, 3, 7, 8 не більше одного разу, запишіть чотирицифрове число, яке ділилося б на 3 і на 5.
12. Якої найменшої довжини повинна бути дошка, щоб її можна було розрізати без залишків на рівні частини завдовжки як 72 см, так і 96 см?
IV рівень
13. Запишіть усі правильні дроби зі знаменником 16, у яких чисельник і знаменник — взаємно прості числа.
14. Замініть зірочку такою цифрою та знайдіть таке число а, щоб була правильною рівність 280* = 3 •5 • 11 • а.
15. У магазині є ножі та виделки загальною кількістю від 320 до 400 штук. Якщо їх рахувати десятками, то буде ціле число десятків, якщо рахувати дюжинами (по 12), то буде ціле число дюжин. Скільки в магазині виделок і скільки ножів, якщо ножів на 160 менше, ніж виделок?
Математика 6 клас Галина Янченко, Василь Кравчук
Вислано читачами iнтернет-сайту
Онлайн-бібліотека з підручниками і книгами, тести з математики, завдання з математики 6 клас, календарне планування
 конспект уроку і опорний каркас конспект уроку і опорний каркас
 презентація уроку презентація уроку
 акселеративні методи та інтерактивні технології акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями) закриті вправи (тільки для використання вчителями)
 оцінювання
Практика оцінювання
Практика
 задачі та вправи,самоперевірка задачі та вправи,самоперевірка
 практикуми, лабораторні, кейси практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання
Ілюстрації домашнє завдання
Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати реферати
 фішки для допитливих фішки для допитливих
 шпаргалки шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення
 зовнішнє незалежне тестування (ЗНТ) зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні підручники основні і допоміжні
 тематичні свята, девізи тематичні свята, девізи
 статті статті
 національні особливості національні особливості
 словник термінів словник термінів
 інше
Тільки для вчителів інше
Тільки для вчителів
 ідеальні уроки ідеальні уроки
 календарний план на рік календарний план на рік
 методичні рекомендації методичні рекомендації
 програми програми
 обговорення обговорення
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|










