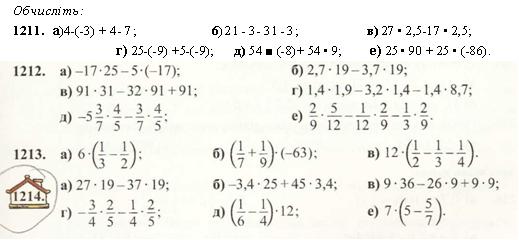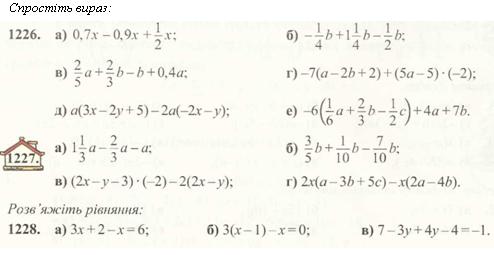|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика]]>>[[Математика 6 клас|Математика 6 клас]]>> Математика: Тема 5.МНОЖЕННЯ І ДІЛЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ . Розподільна властивість множення. Зведення подібних доданків . ''' | + | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика]]>>[[Математика 6 клас|Математика 6 клас]]>>Розподільна властивість множення. Зведення подібних доданків. ''' |
| | | | |
| - | Для раціональних чисел справджується розподільна властивість множення відносно додавання:<br>Для будь-яких раціональних чисел а, Ь і с справджується рівність:<br>(а + b)с = ас + bс.<br>Перевіримо цю рівність, узявши, наприклад, а =-4; 6 = 7; с = -5:<br>(-4 + 7) • (-5) = 3 • (-5) = -15; -4 • (-5) + 7 • (-5) = 20 + (-35) = -15.<br>Отже, (-4 + 7) • (-5) = -4 • (-5) + 7 • (-5).<br>Заміну виразу (а + Ь)с на вираз ас + Ьс або виразу с(а + 6) на вираз са +сЬ називають розкриттям дужок. Наприклад:<br>-5 • (2а + 36) = -5 • 2а + (-5) • 36 = -10а - 156.<br>Заміну виразу ас + Ьс на вираз (а + Ь)с або виразу са + сЬ на вираз с(а + 6) називають винесенням спільного множника за дужки. Наприклад: 36-96 + 26=3 -6-9 -6 + 2 -6 = (3-9 + 2) -6 = -46.<br>У виразі 36-96 + 26 доданки 36,-96 і 26 називають подібними. Подібні доданки мають однакову буквену частину і можуть відрізнятися один від одного лише коефіцієнтами.<br>Записавши вираз 36-96 + 26 у вигляді -46, ми додали або, ще кажуть, звели подібні доданки. При цьому коефіцієнт -4 у виразі -46 дорівнює сумі коефіцієнтів доданків 36, -96 і 26 (3 + (-9) + 2 = -4).<br>Щоб звести подібні доданки, потрібно додати їх коефіцієнти і результат помножити на спільну буквену частину.<br>У виразі може бути кілька груп подібних доданків. При спрощенні таких виразів потрібно спочатку виділити групи подібних доданків, а потім у кожній групі звести подібні. Наприклад:<br>4а -56 + 3 -2а -36 = 2а -86 + 3.<br><br><br>Прочитайте<br><br>1. Розкрити дужки і звести подібні доданки:<br>а) 3(5с -4) -2(3 - 2с); б) -(х + 3) -3(-2х + 3).<br>• а) 3(5с-4)-2(3-2с)= 15с-12-6 +4с= 19с-18:<br>б)-(х + 3)-3(-2х + 3) = -х-3 + 6х-9 = 5х-12. *<br> <br>2. Розв'язати рівняння:<br>а)5х-3х=4; б) 3(2х + 3) - (5л + 2) = 0.<br>• а)5х-3х = 4; 2х = 4; х = 4:2; х = 2.<br>б)3(2х + 3)-(5х + 2) = 0; 6х + 9-5х-2 = 0; х+7 = 0;х = 0-7; х = -7. •<br>3. У виразі 2аЬ + 4ас винести спільний множник за дужки.<br>• 2аЬ + 4ас = 2а • Ь + 2а • 2с = 2а(Ь + 2с). •<br><br>Усно<br><br>1209. Назвіть подібні доданки у виразі:<br>а) х - 2у + Зх-у; б) 1Ь—а-2аЬ + Ь + ЗаЬ.<br>1210. Зведіть подібні доданки:<br>а)5х-4х; б) 4а-а; в) 5х-7х; г)4а-5а + а.<br><br>Рівень А<br><br>
| |
| | | | |
| - | [[Image:Asd314.jpg]]<br>
| + | Для раціональних чисел справджується розподільна властивість множення відносно додавання. |
| | | | |
| - | Розкрийте дужки:<br>1215. я)(х-у)-5; б) (а + Ь-с)-4; в)(2х-у)• (-3);<br> г)-2а(Ь + 2с-Зт): д)-а(6b-5с): е) (-а + ЗЬ + с) • (-2х).<br> <br><br>1216.<br> а)З(а-с); б)-6(2а + 6); в) (-4а-36) • 5;<br>г)а(ЗЬ-4с): д) (х + у-г)• (-а): е)-5а(-26 + 4с-а).<br> <br>Винесіть за дужки спільний множник:<br>1217. а)7х + 7у; б) 15х-10г; в) \0т тк\<br>г)\6а + 8аЬ; д)4аЬ + 6ас; е) Зта- 6тЬ- бтс.<br> <br>1218. а) 10m - 15n; б) 12ad+4d; в) 4mk-10mp.<br> <br>1219. Винесіть за дужки спільний множник і виконайте дії:<br>а) 15-19 + 30-3; 6)90-7-60-8; в) 50• 17 + 25 • 3.<br>Зведіть подібні доданки:<br> <br>1220.<br> а) 9а - 13а + 2а; 6) 5а- 6а + 2а -10а; в) -9х + їх - 5х + 2х;<br> г) 2,86-6 + 2,8/3-/3; ц)-4х-7-5х+\0х; е) 5а +6-76 +За;<br> є)-7а +5а-х-6х; ж) 12х-11+4а-7х; з) 8а-9х + 4-а+х.<br><br><br>1221.<br>а)3с + 7с-8с; б) 16а-5а + 7а-Па; в) -4/+Зґ-8-7ґ;<br>г) 8х-8у + 2у-6х; д) 4,5а-76-1,5а+1; е) -а + 36-46+ 1,5а.<br><br>1223.<br> <br>а) 3(-2х + 5) + 4(х- 2); 6) -(2а - 3) - 2(3а - 1);<br>в)-5(-Зх + 2)-(9-х); г) (36- 1) • (-5) + (4 + 6) • (-2).<br>а) (5х- 3) • 2 - 5(3 - 2х); 6) -(За- 2) + 5(а - 2).<br> <br>1224. Спростіть вираз і знайдіть його значення:<br>а) -5(с + 2) - (2с - 3), якщо с = 1,5;<br>б) 4х-3а-5х + 4а, якщо а =-0,27; х = 0,07.<br>1225. Обчисліть, використовуючи розподільну властивість множення:<br>а)-23-(-99); 6) 98-(-11); в) 999-(-17).<br> [[Image:Asd315.jpg]]
| + | <br>Для будь-яких раціональних чисел а, Ь і с справджується рівність:<br>(а + b)с = ас + bс. |
| | | | |
| - | 1229.<br> <br>а) 7х-8-6х + 3=-5; б) 4(х-5)-Зх + 6 = -2.<br> <br><br>1230. Винесіть за дужки спільний множник:<br>а) 54ху - 63хг; б) 1 ОаЬ -15Ьс-25Ь; в) 42ах - Юау - Маг.<br>Обчисліть раціонально:<br>1231. а) 78-62 + 13-78-75-68; б) 54 • 36-42 • 54 + 6 • 74;<br> в) 478 • 27 + 28 • 478 - 678 -55; г) 4,8 • 6,5 - 8,5 • 6,8 + 2 • 4,8.<br> <br>1232. а) 36-28 + 36-39-67-46; б) 3,4-4,5-3,4-10,6 + 6,1 -4,4.<br> <br><br><br> Здогадайтеся<br><br>1233. Оля в 6 разів молодша від свого прадіда. Вона помітила, що коли між цифрами числа її віку поставити нуль, то буде записано вік прадіда. Скільки років Олі?<br><br><br> Вправи для повторення<br><br>1234. Перший робітник може виконати замовлення за 6 днів, а другий — за 15 днів. Спочатку 2 дні над замовленням працював перший робітник, а потім роботу закінчив другий. Скільки днів працював другий робітник?<br>1235*. Із двох міст виїхали одночасно назустріч один одному два автомобілі. За<br> год перший автомобіль проїхав 1/6 шляху між містами, а другий <br>1/4 цього шляху. Через який час після виїзду автомобілі зустрінуться? Знайдіть швидкість кожного автомобіля, якщо перший автомобіль до місця зустрічі проїхав 144 км.<br>1236. Знайдіть значення виразу:<br>а) (Зх)<sup>2</sup>, якщо х = 2; х = -2; б) а<sup>3</sup> - 12, якщо а = -2; а = 3.<br>1237. а) Добуток двох чисел дорівнює 2, а одне з них — 8. Знайдіть інше число.<br>б) Знайдіть ділене, якщо дільник дорівнює 3,75, а частка — 4.<br>в) Знайдіть дільник, якщо ділене дорівнює 3,75, а частка — 0,25.<br>
| + | <br>Перевіримо цю рівність, узявши, наприклад, а =-4; 6 = 7; с = -5:<br>(-4 + 7) • (-5) = 3 • (-5) = -15; -4 • (-5) + 7 • (-5) = 20 + (-35) = -15.<br>Отже, (-4 + 7) • (-5) = -4 • (-5) + 7 • (-5). |
| | | | |
| - | <br> <sub>[[Гіпермаркет Знань - перший в світі!|Онлайн-бібліотека з підручниками]] і книгами, тести [[Математика|з математики]], завдання [[Математика 6 клас|з математики 6 клас]], календарне планування</sub><br> Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту | + | <br>Заміну виразу (а + Ь)с на вираз ас + Ьс або виразу с(а + 6) на вираз са +сЬ називають розкриттям дужок. Наприклад:<br>-5 • (2а + 36) = -5 • 2а + (-5) • 36 = -10а - 156. |
| | | | |
| - | [[Image:1236084776 kr.jpg|10x10px]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B2%D0%B8%D1%87%D0%B0%D0%B9%D0%BD%D0%B8%D1%85_%D0%B4%D1%80%D0%BE%D0%B1%D1%96%D0%B2._%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D1%83_%D1%96_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%B8%D0%B9_%D0%BA%D0%B0%D1%80%D0%BA%D0%B0%D1%81 конспект уроку і опорний каркас] | + | <br>Заміну виразу ас + Ьс на вираз (а + Ь)с або виразу са + сЬ на вираз с(а + 6) називають винесенням спільного [[Розклад_многочленів_на_множники._Винесення_спільного_множника_за_дужки._Задачі_та_вправи|множник]]а за дужки. Наприклад: 36-96 + 26=3 -6-9 -6 + 2 -6 = (3-9 + 2) -6 = -46. |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентація уроку | + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративні методи та інтерактивні технології | + | <br>У виразі 36-96 + 26 доданки 36,-96 і 26 називають подібними. Подібні доданки мають однакову буквену частину і можуть відрізнятися один від одного лише коефіцієнтами. |
| - | [[Image:1236084776 kr.jpg|10x10px]] закриті вправи (тільки для використання вчителями) | + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] оцінювання | + | <br>Записавши вираз 36-96 + 26 у вигляді -46, ми додали або, ще кажуть, звели подібні доданки. При цьому коефіцієнт -4 у виразі -46 дорівнює сумі коефіцієнтів доданків 36, -96 і 26 (3 + (-9) + 2 = -4). |
| | + | |
| | + | <br>Щоб звести подібні [[Розкладання_на_розрядні_доданки._Фішки_для_допитливих|доданки]], потрібно додати їх коефіцієнти і результат помножити на спільну буквену частину.<br>У виразі може бути кілька груп подібних доданків. При спрощенні таких виразів потрібно спочатку виділити групи подібних доданків, а потім у кожній групі звести подібні. Наприклад:<br>4а -56 + 3 -2а -36 = 2а -86 + 3.<br><br>'''Прочитайте'''<br>1. Розкрити дужки і звести подібні доданки:<br>а) 3(5с -4) -2(3 - 2с); б) -(х + 3) -3(-2х + 3).<br>• а) 3(5с-4)-2(3-2с)= 15с-12-6 +4с= 19с-18:<br>б)-(х + 3)-3(-2х + 3) = -х-3 + 6х-9 = 5х-12. *<br> <br>2. Розв'язати рівняння:<br>а)5х-3х=4; б) 3(2х + 3) - (5л + 2) = 0.<br>а)5х-3х = 4; 2х = 4; х = 4:2; х = 2.<br>б)3(2х + 3)-(5х + 2) = 0; 6х + 9-5х-2 = 0; х+7 = 0;х = 0-7; х = -7. |
| | + | |
| | + | <br>3. У виразі 2аЬ + 4ас винести спільний множник за дужки.<br>2аЬ + 4ас = 2а • Ь + 2а • 2с = 2а(Ь + 2с).<br><br>'''Усно'''<br>1209. Назвіть подібні доданки у виразі:<br>а) х - 2у + Зх-у; б) 1Ь—а-2аЬ + Ь + ЗаЬ. |
| | + | |
| | + | <br>1210. Зведіть подібні доданки:<br>а)5х-4х; б) 4а-а; в) 5х-7х; г)4а-5а + а.<br><br>Рівень А<br><br> |
| | + | |
| | + | [[Image:Asd314.jpg|450px|Рівень А]]<br> |
| | + | |
| | + | Розкрийте [[Розклад_многочленів_на_множники._Винесення_спільного_множника_за_дужки._Повні_уроки|дужки]]:<br>1215. я)(х-у)-5; б) (а + Ь-с)-4; в)(2х-у)• (-3);<br> г)-2а(Ь + 2с-Зт): д)-а(6b-5с): е) (-а + ЗЬ + с) • (-2х).<br> <br>1216.<br> а)З(а-с); б)-6(2а + 6); в) (-4а-36) • 5;<br>г)а(ЗЬ-4с): д) (х + у-г)• (-а): е)-5а(-26 + 4с-а).<br> <br>Винесіть за дужки спільний множник:<br>1217. а)7х + 7у; б) 15х-10г; в) \0т тк\<br>г)\6а + 8аЬ; д)4аЬ + 6ас; е) Зта- 6тЬ- бтс.<br> <br>1218. а) 10m - 15n; б) 12ad+4d; в) 4mk-10mp.<br> <br>1219. Винесіть за дужки спільний множник і виконайте дії:<br>а) 15-19 + 30-3; 6)90-7-60-8; в) 50• 17 + 25 • 3. |
| | + | |
| | + | <br>Зведіть подібні доданки:<br> <br>1220.<br> а) 9а - 13а + 2а; 6) 5а- 6а + 2а -10а; в) -9х + їх - 5х + 2х;<br> г) 2,86-6 + 2,8/3-/3; ц)-4х-7-5х+\0х; е) 5а +6-76 +За;<br> є)-7а +5а-х-6х; ж) 12х-11+4а-7х; з) 8а-9х + 4-а+х.<br><br>1221.<br>а)3с + 7с-8с; б) 16а-5а + 7а-Па; в) -4/+Зґ-8-7ґ;<br>г) 8х-8у + 2у-6х; д) 4,5а-76-1,5а+1; е) -а + 36-46+ 1,5а.<br><br>1223.<br> а) 3(-2х + 5) + 4(х- 2); 6) -(2а - 3) - 2(3а - 1);<br>в)-5(-Зх + 2)-(9-х); г) (36- 1) • (-5) + (4 + 6) • (-2).<br>а) (5х- 3) • 2 - 5(3 - 2х); 6) -(За- 2) + 5(а - 2).<br> <br>1224. Спростіть вираз і знайдіть його значення:<br>а) -5(с + 2) - (2с - 3), якщо с = 1,5;<br>б) 4х-3а-5х + 4а, якщо а =-0,27; х = 0,07. |
| | + | |
| | + | <br>1225. Обчисліть, використовуючи розподільну властивість множення:<br>а)-23-(-99); 6) 98-(-11); в) 999-(-17). |
| | + | |
| | + | <br> [[Image:Asd315.jpg|450px|Обчисліть]] |
| | + | |
| | + | 1229. а) 7х-8-6х + 3=-5; б) 4(х-5)-Зх + 6 = -2.<br> <br>1230. Винесіть за дужки спільний множник:<br>а) 54ху - 63хг; б) 1 ОаЬ -15Ьс-25Ь; в) 42ах - Юау - Маг. |
| | + | |
| | + | <br>Обчисліть раціонально:<br>1231. а) 78-62 + 13-78-75-68; б) 54 • 36-42 • 54 + 6 • 74;<br> в) 478 • 27 + 28 • 478 - 678 -55; г) 4,8 • 6,5 - 8,5 • 6,8 + 2 • 4,8.<br> <br>1232. а) 36-28 + 36-39-67-46; б) 3,4-4,5-3,4-10,6 + 6,1 -4,4.<br> <br>'''Здогадайтеся'''<br>1233. Оля в 6 разів молодша від свого прадіда. Вона помітила, що коли між цифрами числа її віку поставити [[Урок_16._Нуль|нуль]], то буде записано вік прадіда. Скільки років Олі?<br><br>'''Вправи для повторення'''<br>1234. Перший робітник може виконати замовлення за 6 днів, а другий — за 15 днів. Спочатку 2 дні над замовленням працював перший робітник, а потім роботу закінчив другий. Скільки днів працював другий робітник? |
| | + | |
| | + | <br>1235*. Із двох міст виїхали одночасно назустріч один одному два автомобілі. За год перший автомобіль проїхав 1/6 шляху між містами, а другий 1/4 цього шляху. Через який час після виїзду автомобілі зустрінуться? Знайдіть [[Види_рухів._Середня_швидкість_нерівномірного_руху._Прямолінійний_рівномірний_рух._Графіки_руху_тіла.|швидкість]] кожного автомобіля, якщо перший автомобіль до місця зустрічі проїхав 144 км. |
| | + | |
| | + | <br>1236. Знайдіть значення виразу:<br>а) (Зх)<sup>2</sup>, якщо х = 2; х = -2; б) а<sup>3</sup> - 12, якщо а = -2; а = 3. |
| | + | |
| | + | <br>1237. а) Добуток двох чисел дорівнює 2, а одне з них — 8. Знайдіть інше число.<br>б) Знайдіть ділене, якщо дільник дорівнює 3,75, а частка — 4.<br>в) Знайдіть дільник, якщо ділене дорівнює 3,75, а частка — 0,25.<br> |
| | + | |
| | + | |
| | + | |
| | + | [[Математика_6_клас|''Математика 6 клас'']]''Галина Янченко, Василь Кравчук '' |
| | + | |
| | + | ''Вислано читачами iнтернет-сайту'' |
| | + | |
| | + | <br> <sub>[[Гіпермаркет Знань - перший в світі!|Онлайн-бібліотека з підручниками]] і книгами, тести [[Математика|з математики]], завдання [[Математика 6 клас|з математики 6 клас]], календарне планування</sub> |
| | + | |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B2%D0%B8%D1%87%D0%B0%D0%B9%D0%BD%D0%B8%D1%85_%D0%B4%D1%80%D0%BE%D0%B1%D1%96%D0%B2._%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D1%83_%D1%96_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%B8%D0%B9_%D0%BA%D0%B0%D1%80%D0%BA%D0%B0%D1%81 конспект уроку і опорний каркас] |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентація уроку |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративні методи та інтерактивні технології |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] закриті вправи (тільки для використання вчителями) |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] оцінювання |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачі та вправи,самоперевірка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%A0%D0%BE%D0%B7%D0%BF%D0%BE%D0%B4%D1%96%D0%BB%D1%8C%D0%BD%D0%B0_%D0%B2%D0%BB%D0%B0%D1%81%D1%82%D0%B8%D0%B2%D1%96%D1%81%D1%82%D1%8C_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F._%D0%97%D0%B2%D0%B5%D0%B4%D0%B5%D0%BD%D0%BD%D1%8F_%D0%BF%D0%BE%D0%B4%D1%96%D0%B1%D0%BD%D0%B8%D1%85_%D0%B4%D0%BE%D0%B4%D0%B0%D0%BD%D0%BA%D1%96%D0%B2._%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D1%96_%D1%82%D0%B0_%D0%B2%D0%BF%D1%80%D0%B0%D0%B2%D0%B8,%D1%81%D0%B0%D0%BC%D0%BE%D0%BF%D0%B5%D1%80%D0%B5%D0%B2%D1%96%D1%80%D0%BA%D0%B0 задачі та вправи,самоперевірка] |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикуми, лабораторні, кейси | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикуми, лабораторні, кейси |
| - | [[Image:1236084776 kr.jpg|10x10px]] рівень складності задач: звичайний, високий, олімпійський | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рівень складності задач: звичайний, високий, олімпійський |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашнє завдання | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашнє завдання |
| | | | |
| | '''<u>Ілюстрації</u>''' | | '''<u>Ілюстрації</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа |
| - | [[Image:1236084776 kr.jpg|10x10px]] реферати | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] реферати |
| - | [[Image:1236084776 kr.jpg|10x10px]] фішки для допитливих | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фішки для допитливих |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] гумор, притчі, приколи, приказки, кросворди, цитати | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] гумор, притчі, приколи, приказки, кросворди, цитати |
| | | | |
| | '''<u>Доповнення</u>''' | | '''<u>Доповнення</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] зовнішнє незалежне тестування (ЗНТ) | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] зовнішнє незалежне тестування (ЗНТ) |
| - | [[Image:1236084776 kr.jpg|10x10px]] підручники основні і допоміжні | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] підручники основні і допоміжні |
| - | [[Image:1236084776 kr.jpg|10x10px]] тематичні свята, девізи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] тематичні свята, девізи |
| - | [[Image:1236084776 kr.jpg|10x10px]] статті | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статті |
| - | [[Image:1236084776 kr.jpg|10x10px]] національні особливості | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] національні особливості |
| - | [[Image:1236084776 kr.jpg|10x10px]] словник термінів | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словник термінів |
| - | [[Image:1236084776 kr.jpg|10x10px]] інше | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] інше |
| | | | |
| | '''<u>Тільки для вчителів</u>''' | | '''<u>Тільки для вчителів</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] [http://xvatit.com/Idealny_urok.html ідеальні уроки] | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://xvatit.com/Idealny_urok.html ідеальні уроки] |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарний план на рік | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарний план на рік |
| - | [[Image:1236084776 kr.jpg|10x10px]] методичні рекомендації | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методичні рекомендації |
| - | [[Image:1236084776 kr.jpg|10x10px]] програми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] програми |
| - | [[Image:1236084776 kr.jpg|10x10px]] [http://xvatit.com/forum/ обговорення] | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://xvatit.com/forum/ обговорення] |
| | | | |
| | | | |
Текущая версия на 13:01, 2 ноября 2012
Гіпермаркет Знань>>Математика>>Математика 6 клас>>Розподільна властивість множення. Зведення подібних доданків.
Для раціональних чисел справджується розподільна властивість множення відносно додавання.
Для будь-яких раціональних чисел а, Ь і с справджується рівність:
(а + b)с = ас + bс.
Перевіримо цю рівність, узявши, наприклад, а =-4; 6 = 7; с = -5:
(-4 + 7) • (-5) = 3 • (-5) = -15; -4 • (-5) + 7 • (-5) = 20 + (-35) = -15.
Отже, (-4 + 7) • (-5) = -4 • (-5) + 7 • (-5).
Заміну виразу (а + Ь)с на вираз ас + Ьс або виразу с(а + 6) на вираз са +сЬ називають розкриттям дужок. Наприклад:
-5 • (2а + 36) = -5 • 2а + (-5) • 36 = -10а - 156.
Заміну виразу ас + Ьс на вираз (а + Ь)с або виразу са + сЬ на вираз с(а + 6) називають винесенням спільного множника за дужки. Наприклад: 36-96 + 26=3 -6-9 -6 + 2 -6 = (3-9 + 2) -6 = -46.
У виразі 36-96 + 26 доданки 36,-96 і 26 називають подібними. Подібні доданки мають однакову буквену частину і можуть відрізнятися один від одного лише коефіцієнтами.
Записавши вираз 36-96 + 26 у вигляді -46, ми додали або, ще кажуть, звели подібні доданки. При цьому коефіцієнт -4 у виразі -46 дорівнює сумі коефіцієнтів доданків 36, -96 і 26 (3 + (-9) + 2 = -4).
Щоб звести подібні доданки, потрібно додати їх коефіцієнти і результат помножити на спільну буквену частину.
У виразі може бути кілька груп подібних доданків. При спрощенні таких виразів потрібно спочатку виділити групи подібних доданків, а потім у кожній групі звести подібні. Наприклад:
4а -56 + 3 -2а -36 = 2а -86 + 3.
Прочитайте
1. Розкрити дужки і звести подібні доданки:
а) 3(5с -4) -2(3 - 2с); б) -(х + 3) -3(-2х + 3).
• а) 3(5с-4)-2(3-2с)= 15с-12-6 +4с= 19с-18:
б)-(х + 3)-3(-2х + 3) = -х-3 + 6х-9 = 5х-12. *
2. Розв'язати рівняння:
а)5х-3х=4; б) 3(2х + 3) - (5л + 2) = 0.
а)5х-3х = 4; 2х = 4; х = 4:2; х = 2.
б)3(2х + 3)-(5х + 2) = 0; 6х + 9-5х-2 = 0; х+7 = 0;х = 0-7; х = -7.
3. У виразі 2аЬ + 4ас винести спільний множник за дужки.
2аЬ + 4ас = 2а • Ь + 2а • 2с = 2а(Ь + 2с).
Усно
1209. Назвіть подібні доданки у виразі:
а) х - 2у + Зх-у; б) 1Ь—а-2аЬ + Ь + ЗаЬ.
1210. Зведіть подібні доданки:
а)5х-4х; б) 4а-а; в) 5х-7х; г)4а-5а + а.
Рівень А
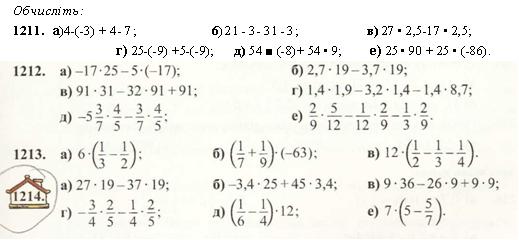
Розкрийте дужки:
1215. я)(х-у)-5; б) (а + Ь-с)-4; в)(2х-у)• (-3);
г)-2а(Ь + 2с-Зт): д)-а(6b-5с): е) (-а + ЗЬ + с) • (-2х).
1216.
а)З(а-с); б)-6(2а + 6); в) (-4а-36) • 5;
г)а(ЗЬ-4с): д) (х + у-г)• (-а): е)-5а(-26 + 4с-а).
Винесіть за дужки спільний множник:
1217. а)7х + 7у; б) 15х-10г; в) \0т тк\
г)\6а + 8аЬ; д)4аЬ + 6ас; е) Зта- 6тЬ- бтс.
1218. а) 10m - 15n; б) 12ad+4d; в) 4mk-10mp.
1219. Винесіть за дужки спільний множник і виконайте дії:
а) 15-19 + 30-3; 6)90-7-60-8; в) 50• 17 + 25 • 3.
Зведіть подібні доданки:
1220.
а) 9а - 13а + 2а; 6) 5а- 6а + 2а -10а; в) -9х + їх - 5х + 2х;
г) 2,86-6 + 2,8/3-/3; ц)-4х-7-5х+\0х; е) 5а +6-76 +За;
є)-7а +5а-х-6х; ж) 12х-11+4а-7х; з) 8а-9х + 4-а+х.
1221.
а)3с + 7с-8с; б) 16а-5а + 7а-Па; в) -4/+Зґ-8-7ґ;
г) 8х-8у + 2у-6х; д) 4,5а-76-1,5а+1; е) -а + 36-46+ 1,5а.
1223.
а) 3(-2х + 5) + 4(х- 2); 6) -(2а - 3) - 2(3а - 1);
в)-5(-Зх + 2)-(9-х); г) (36- 1) • (-5) + (4 + 6) • (-2).
а) (5х- 3) • 2 - 5(3 - 2х); 6) -(За- 2) + 5(а - 2).
1224. Спростіть вираз і знайдіть його значення:
а) -5(с + 2) - (2с - 3), якщо с = 1,5;
б) 4х-3а-5х + 4а, якщо а =-0,27; х = 0,07.
1225. Обчисліть, використовуючи розподільну властивість множення:
а)-23-(-99); 6) 98-(-11); в) 999-(-17).
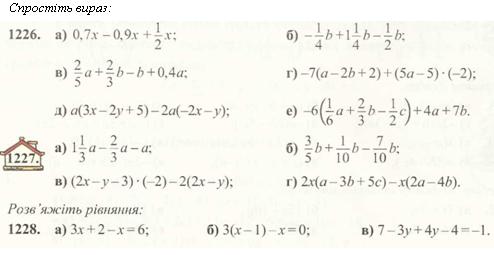
1229. а) 7х-8-6х + 3=-5; б) 4(х-5)-Зх + 6 = -2.
1230. Винесіть за дужки спільний множник:
а) 54ху - 63хг; б) 1 ОаЬ -15Ьс-25Ь; в) 42ах - Юау - Маг.
Обчисліть раціонально:
1231. а) 78-62 + 13-78-75-68; б) 54 • 36-42 • 54 + 6 • 74;
в) 478 • 27 + 28 • 478 - 678 -55; г) 4,8 • 6,5 - 8,5 • 6,8 + 2 • 4,8.
1232. а) 36-28 + 36-39-67-46; б) 3,4-4,5-3,4-10,6 + 6,1 -4,4.
Здогадайтеся
1233. Оля в 6 разів молодша від свого прадіда. Вона помітила, що коли між цифрами числа її віку поставити нуль, то буде записано вік прадіда. Скільки років Олі?
Вправи для повторення
1234. Перший робітник може виконати замовлення за 6 днів, а другий — за 15 днів. Спочатку 2 дні над замовленням працював перший робітник, а потім роботу закінчив другий. Скільки днів працював другий робітник?
1235*. Із двох міст виїхали одночасно назустріч один одному два автомобілі. За год перший автомобіль проїхав 1/6 шляху між містами, а другий 1/4 цього шляху. Через який час після виїзду автомобілі зустрінуться? Знайдіть швидкість кожного автомобіля, якщо перший автомобіль до місця зустрічі проїхав 144 км.
1236. Знайдіть значення виразу:
а) (Зх)2, якщо х = 2; х = -2; б) а3 - 12, якщо а = -2; а = 3.
1237. а) Добуток двох чисел дорівнює 2, а одне з них — 8. Знайдіть інше число.
б) Знайдіть ділене, якщо дільник дорівнює 3,75, а частка — 4.
в) Знайдіть дільник, якщо ділене дорівнює 3,75, а частка — 0,25.
Математика 6 класГалина Янченко, Василь Кравчук
Вислано читачами iнтернет-сайту
Онлайн-бібліотека з підручниками і книгами, тести з математики, завдання з математики 6 клас, календарне планування
 конспект уроку і опорний каркас конспект уроку і опорний каркас
 презентація уроку презентація уроку
 акселеративні методи та інтерактивні технології акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями) закриті вправи (тільки для використання вчителями)
 оцінювання
Практика оцінювання
Практика
 задачі та вправи,самоперевірка задачі та вправи,самоперевірка
 практикуми, лабораторні, кейси практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання
Ілюстрації домашнє завдання
Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати реферати
 фішки для допитливих фішки для допитливих
 шпаргалки шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення
 зовнішнє незалежне тестування (ЗНТ) зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні підручники основні і допоміжні
 тематичні свята, девізи тематичні свята, девізи
 статті статті
 національні особливості національні особливості
 словник термінів словник термінів
 інше
Тільки для вчителів інше
Тільки для вчителів
 ідеальні уроки ідеальні уроки
 календарний план на рік календарний план на рік
 методичні рекомендації методичні рекомендації
 програми програми
 обговорення обговорення
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|