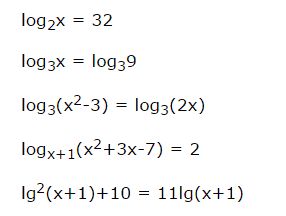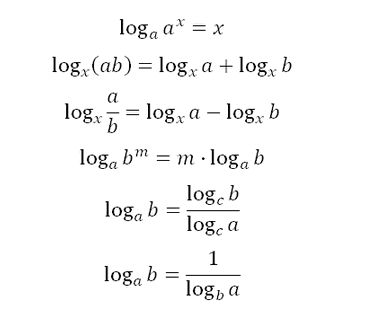|
|
|
| (5 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>>Математика: Логарифмические уравнения<metakeywords>Логарифмические уравнения</metakeywords>'''
| + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 10 класс, урок, на Тему, Логарифмические уравнения, корни, логарифм, неравенства</metakeywords> |
| | | | |
| - | А.Г. Мордкович Алгебра 10 класс
| + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>> Логарифмические уравнения''' |
| | | | |
| - | <br> | + | <h2>Что такое логарифмическое уравнение?</h2> |
| | | | |
| - | <sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub>
| + | Логарифмическим уравнением называют такое уравнение, в котором неизвестная представлена под знаком логарифма. |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | То есть, если говорить более понятным языком, то в логарифмическом уравнении все неизвестные х, а также выражения с ними, расположены внутри логарифмов. |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | Теперь давайте рассмотрим примеры логарифмических уравнений: |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | [[Image:10kl_Logarifm01.jpg|300x300px|логарифм]] |
| | + | <br> |
| | | | |
| - | '''<u>Практика</u>'''
| + | Если вы внимательно посмотрите на примере этих разнообразных уравнений, то заметите, что выражения с неизвестными х расположены, все без исключения, внутри логарифмов. |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | Но бывают такие случаи, когда в уравнении, внутри логарифмов не наблюдается присутствия х, а есть только числа. Например: |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | х+2 = lg8+lg50 |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | Если вам попалось такое уравнение, то можно сказать, что вам повезло. Ведь логарифм с числами - это какое-то число и чтобы решить такое уравнение, достаточно хорошо понимать свойства логарифмов. В этом случае не требуется особых ни знаний каких-то определенных правил, ни особых приемов. |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | <br> |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | [[Image:10kl_Logarifm02.jpg|500x500px|логарифм]] |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | |
| | | | |
| - | '''<u>Дополнения</u>'''
| + | <h2>Как решать простейшие логарифмические уравнения?</h2> |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| - |
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| | + | Существует довольно много различных методов решения логарифмических уравнений. К таким способам относится такие своеобразные подходы, как разложение на множители, замена, потенцирование, а также работа с основаниями. |
| | + | |
| | + | Но какой бы способ решения логарифмического уравнения вы не выбрали, следует знать, что все решения этих уравнений сводятся к тому, что любое логарифмическое уравнение необходимо привести к его простейшему виду: |
| | + | |
| | + | loga(f(x)) = loga(g(x)), |
| | + | |
| | + | После того, как вы свели уравнение к такому виду, можете приступать к решению уравнения без логарифмов: |
| | + | |
| | + | f(x)=g(x). |
| | + | |
| | + | То есть, чтобы вам было еще более понятно, то следует запомнить, что весь процесс решения любого логарифмического уравнения сводится к тому, что необходимо перейти от уравнения с логарифмами к уравнению, где логарифмы отсутствуют. |
| | + | |
| | + | В простых логарифмических уравнениях такой переход осуществляется довольно просто. |
| | + | Давайте рассмотрим этот процесс на примере. |
| | + | |
| | + | Вот мы с вами имеем простое логарифмическое уравнение: |
| | + | |
| | + | log3х = log39 |
| | + | |
| | + | Чтобы получить уравнение без логарифмов, нам необходимо от них избавиться. В этом случае алгебра нам позволяет логарифмы убрать, и вот что в итоге мы получим: |
| | + | |
| | + | х = 9 |
| | + | |
| | + | Убрать логарифмы таким методом, является одним из основных способов решения логарифмических уравнений или неравенств. Такая своеобразная операция избавления от логарифмов называется потенцирование. |
| | + | |
| | + | Но даже на такую ликвидацию логарифмов существуют определенные правила. |
| | + | |
| | + | Без проблем и опасений убрать логарифмы можно в том случае, если: |
| | + | |
| | + | • Во-первых, они имеют одинаковые числовые основания;<br> |
| | + | • Во-вторых, что слева, что справа, логарифмы должны быть без всяких коэффициентов, то есть, находится в гордом одиночестве;<br> |
| | + | |
| | + | Но следует учесть, что при решении уравнений с логарифмами не всегда есть возможность от логарифма избавиться. Так, например, в уравнении: |
| | + | |
| | + | log3х = 2log3(3х-1) |
| | + | |
| | + | Убрать логарифм в этом случае не позволяет двойка, которая стоит справа, так как она является коэффициентом. |
| | + | |
| | + | А если рассмотреть следующий пример, то это уравнение также нельзя потенцировать, так как у него слева не наблюдается одинокого логарифма: |
| | + | |
| | + | log3х+log3(х+1) = log3(3+х) |
| | + | |
| | + | Вот мы и пришли с вами к такому выводу, что убирать логарифмы можно только тогда, когда уравнение имеет соответственный вид: |
| | + | |
| | + | logа(.....) = logа(.....) |
| | + | |
| | + | В этом уравнении в скобках могут быть любые выражения, но важно, чтобы после того, как мы уберем логарифм, у нас осталось более простое уравнение. |
| | + | |
| | + | <h2>Свойства логарифмов</h2> |
| | + | |
| | + | <br> |
| | + | [[Image:10kl_Logarifm03.jpg|400x400px|логарифм]] |
| | <br> | | <br> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | <h2>Следует знать</h2> |
| | + | |
| | + | На этом уроке мы с вами рассмотрели решение простейших логарифмических уравнений и можем с уверенностью сказать, что никаких сложных преобразований мы не наблюдали. |
| | + | |
| | + | Но для успешного решения таких задач важно знать свойства логарифма и понимать основное логарифмическое тождество. |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | Также, следует запомнить, что после того, как будет найден корень логарифмического уравнения, необходимо в обязательном порядке делать проверку полученных корней. |
Текущая версия на 12:08, 20 августа 2015
Гипермаркет знаний>>Математика>>Математика 10 класс>> Логарифмические уравнения
Что такое логарифмическое уравнение?
Логарифмическим уравнением называют такое уравнение, в котором неизвестная представлена под знаком логарифма.
То есть, если говорить более понятным языком, то в логарифмическом уравнении все неизвестные х, а также выражения с ними, расположены внутри логарифмов.
Теперь давайте рассмотрим примеры логарифмических уравнений:
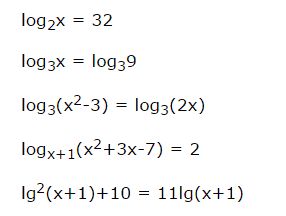
Если вы внимательно посмотрите на примере этих разнообразных уравнений, то заметите, что выражения с неизвестными х расположены, все без исключения, внутри логарифмов.
Но бывают такие случаи, когда в уравнении, внутри логарифмов не наблюдается присутствия х, а есть только числа. Например:
х+2 = lg8+lg50
Если вам попалось такое уравнение, то можно сказать, что вам повезло. Ведь логарифм с числами - это какое-то число и чтобы решить такое уравнение, достаточно хорошо понимать свойства логарифмов. В этом случае не требуется особых ни знаний каких-то определенных правил, ни особых приемов.

Как решать простейшие логарифмические уравнения?
Существует довольно много различных методов решения логарифмических уравнений. К таким способам относится такие своеобразные подходы, как разложение на множители, замена, потенцирование, а также работа с основаниями.
Но какой бы способ решения логарифмического уравнения вы не выбрали, следует знать, что все решения этих уравнений сводятся к тому, что любое логарифмическое уравнение необходимо привести к его простейшему виду:
loga(f(x)) = loga(g(x)),
После того, как вы свели уравнение к такому виду, можете приступать к решению уравнения без логарифмов:
f(x)=g(x).
То есть, чтобы вам было еще более понятно, то следует запомнить, что весь процесс решения любого логарифмического уравнения сводится к тому, что необходимо перейти от уравнения с логарифмами к уравнению, где логарифмы отсутствуют.
В простых логарифмических уравнениях такой переход осуществляется довольно просто.
Давайте рассмотрим этот процесс на примере.
Вот мы с вами имеем простое логарифмическое уравнение:
log3х = log39
Чтобы получить уравнение без логарифмов, нам необходимо от них избавиться. В этом случае алгебра нам позволяет логарифмы убрать, и вот что в итоге мы получим:
х = 9
Убрать логарифмы таким методом, является одним из основных способов решения логарифмических уравнений или неравенств. Такая своеобразная операция избавления от логарифмов называется потенцирование.
Но даже на такую ликвидацию логарифмов существуют определенные правила.
Без проблем и опасений убрать логарифмы можно в том случае, если:
• Во-первых, они имеют одинаковые числовые основания;
• Во-вторых, что слева, что справа, логарифмы должны быть без всяких коэффициентов, то есть, находится в гордом одиночестве;
Но следует учесть, что при решении уравнений с логарифмами не всегда есть возможность от логарифма избавиться. Так, например, в уравнении:
log3х = 2log3(3х-1)
Убрать логарифм в этом случае не позволяет двойка, которая стоит справа, так как она является коэффициентом.
А если рассмотреть следующий пример, то это уравнение также нельзя потенцировать, так как у него слева не наблюдается одинокого логарифма:
log3х+log3(х+1) = log3(3+х)
Вот мы и пришли с вами к такому выводу, что убирать логарифмы можно только тогда, когда уравнение имеет соответственный вид:
logа(.....) = logа(.....)
В этом уравнении в скобках могут быть любые выражения, но важно, чтобы после того, как мы уберем логарифм, у нас осталось более простое уравнение.
Свойства логарифмов
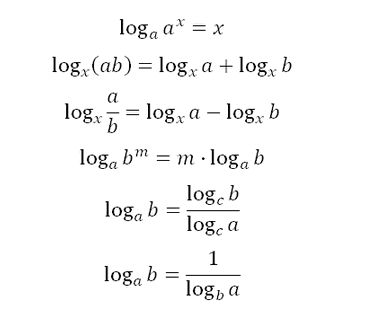
Следует знать
На этом уроке мы с вами рассмотрели решение простейших логарифмических уравнений и можем с уверенностью сказать, что никаких сложных преобразований мы не наблюдали.
Но для успешного решения таких задач важно знать свойства логарифма и понимать основное логарифмическое тождество.
Также, следует запомнить, что после того, как будет найден корень логарифмического уравнения, необходимо в обязательном порядке делать проверку полученных корней.
|