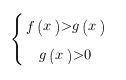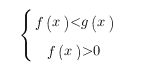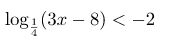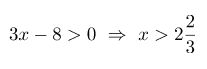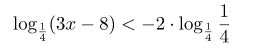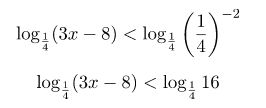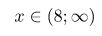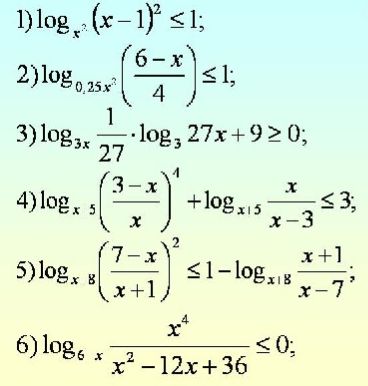|
|
|
| (16 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>>Математика: Логарифмические неравенства<metakeywords>Логарифмические неравенства</metakeywords>'''
| + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 10 класс, урок, на Тему, Логарифмические неравенства, логарифм, переменная</metakeywords> |
| | | | |
| | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>> Логарифмические неравенства''' |
| | | | |
| | + | <h2>Логарифмические неравенства</h2> |
| | | | |
| - | '''§ 52. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА'''<br>Логарифмическими неравенствами называют неравенства вида
| + | На предыдущих уроках мы с вами познакомились с логарифмическими уравнениями и теперь знаем, что это такое и как их решать. А сегодняшний урок будет посвящен изучению логарифмических неравенств. Что же это за такие неравенства и в чем разница между решением логарифмического уравнения и неравенства? |
| | | | |
| - | [[Image:a10219.jpg]]<br>где а — положительное число, отличное от 1, и неравенства, сводящиеся к этому виду.<br>Для решения неравенства (1) проведем следующие рассуждения: преобразуем неравенство к виду
| + | Логарифмические неравенства - это неравенства, которые имеют переменную, стоящую под знаком логарифма или в его основании. |
| | | | |
| - | [[Image:a10220.jpg]]
| + | Или же, можно еще сказать, что логарифмическое неравенство – это такое неравенство, в котором его неизвестная величина, как и в логарифмическом уравнении, будет стоять под знаком логарифма. |
| | | | |
| - | Теперь следует рассмотреть два случая: а>1 и 0<а<1. Если а > 1, то неравенство log<sub>a</sub> t >0 имеет место тогда и только тогда, когда (см. § 49, рис. 216). Значит,
| + | Простейшие логарифмические неравенства имеют такой вид: |
| | | | |
| - | [[Image:a10221.jpg]] | + | <br> |
| | + | [[Image:10kl_LogNer01.jpg|200x200px|лог.неравенства]] |
| | + | <br> |
| | | | |
| - | Если 0 < а < 1, то неравенство log<sub>a</sub> t > 1 имеет место тогда и только тогда, когда 0 <t<1 (см. § 49, рис. 217). Значит,
| + | где f(x) и g(x) являются некоторыми выражениями, которые зависят от x. |
| | | | |
| - | [[Image:a10222.jpg]]
| + | Давайте это рассмотрим на таком примере: f(x)=1+2x+x2, g(x)=3x−1. |
| | | | |
| - | Проведенные рассуждения позволяют сформулировать следующее утверждение.
| + | <h2>Решение логарифмических неравенств</h2> |
| | | | |
| - | [[Image:a10223.jpg]]<br>На практике эту теорему применяют так: переходят от неравенства [[Image:a10224.jpg]] к равносильной ему системе неравенств:
| + | Перед решением логарифмических неравенств, стоит отметить, что они при решении имеют сходство с показательными неравенствами, а именно: |
| | | | |
| - | [[Image:a10225.jpg]]<br>Первые два неравенства каждой из этих систем определяют область допустимых значений переменной для неравенства (1), а знак последнего неравенства каждой из систем (обратите внимание!) либо совпадает со знаком неравенства (1) — в случае, когда а> 1, — либо противоположен знаку неравенства (1) — в случае, когда0 <а <1.<br>'''Пример 1.''' Решить неравенства:
| + | • Во-первых, при переходе от логарифмов к выражениям, стоящим под знаком логарифма, нам также необходимо сравнить основание логарифма с единицей;<br> |
| | | | |
| - | <br>а) 1ое3(2х-4)>1о&3(14-х); б) 1оеД2х -4)> 10^(14 - х).<br>3 3<br>Решение, а) Область допустимых значений переменной для заданного неравенства определяется условиями: 2х-4>0и 14-х>0. Поскольку основанием логарифмов служит число 3, а оно больше 1, то, «освобождаясь» от знаков логарифмов, мы получим неравенство того же смысла: ' 2х-4>14-х.<br>В итоге получаем систему неравенств:<br>|2х-4>0, Ш-х>0, |2х-4>14-х.<br>Из первого неравенства системы находим х >2, из второго — х <14, из третьего — х >6. Геометрическая модель (рис. 226) помогает найти решение системы неравенств: 6 < х < 14.<br>б) Здесь основание логарифма, т.е. число меньше 1. Значит, соответс-<br>3<br>твующая система неравенств имеет вид:<br>2х-4>0,<br>■ 14-х>0, 2х-4<14-х<br> * =1- <br> * 1 / I <br> [ -14- X<br> 1 1 I <br> <br> Л I <br> 1 -14- X<br> 1 I <br>Рис. 226<br>280<br>Рис. 227<br>(обратите внимание: знак последнего неравенства системы противоположен знаку исходного логарифмического неравенства).<br>Из первого неравенства системы находим х > 2, из второго — х <14, из третьего — х <6. Геометрическая модель (рис. 227) помогает найти решение системы неравенств: 2 < х < 6.<br>Ответ: а)6<х<14; 6)2 <х <6.<br>Замечание. Еще раз рассмотрим систему неравенств, которая получилась в примере 1а. Третье неравенство системы имеет вид 2х -4>14-х, а второе —14 - х > 0. Но из этих двух неравенств автоматически (по свойству транзитивности неравенств) следует, что 2х - 4 > 0. Что это значит? Это значит, что первое неравенство системы с самого начала можно было отбросить без всякого ущерба для решения системы.<br>Рассуждая аналогично, в системе неравенств, которую мы получили в примере 16, можно было с самого начала отбросить второе неравенство.<br>Получив систему неравенств, математики обычно смотрят, нет ли в ней неравенства, которое логически следует из других. Если такое неравенство есть, его можно отбросить. Советуем и вам так поступать, но, разумеется, только в том случае, если вы уверены в правильности своих выводов.<br>Пример 2. Решить неравенство: 1ое, (16 + 4х - х2 )< - 4.<br>2 1<br>Решение. Представим -4 в виде логарифма по основанию —:<br>2<br>ГIV4<br>-4 = I — = 16. Это позволит переписать заданное неравенство в<br>IV2; 2<br>виде: 1о{Г, (16 + 4х - х2) < 1о§, 16.<br>2 2<br>Учитывая, что здесь основанием логарифмов служит число, меньше 1,<br>составляем равносильную заданному неравенству систему неравенств:<br>16 + 4х-х2>0,<br>16 + 4х-х2>16. *<br>Обратите внимание: если выполняется второе неравенство системы, то автоматически выполняется и первое неравенство (если А > 16, то тем более А >0). Значит, первое неравенство системы можно отбросить. Решая второе неравенство, находим: х2-4х<0; х(х-4)<0.<br>С помощью метода интервалов (рис. 228) получаем 0<х <4.<br>Ответ: 0<х<4.<br>Пример 3. Решить неравенство 1§х + 1§(45-х)<2 +1§2.<br>Решение. Имеем последовательно:<br>х + 1ё(45 - х)= 1ё х(45 - х) = 1ё(45х - х2), 2+1в2 = 18100+1ё2 = 1ё100-2 = 1§200.<br>Значит, заданное неравенство можно преобразовать к виду 1ё(45х - х2) < 200.<br>«Освобождаясь» от знаков десятичных логарифмов, получим неравенство того же смысла: 45х - х2 < 200. А условия, задающие область допустимых значений переменной, всегда определяют по исходному неравенству; в данном примере они таковы: х>0и45-х>0. В итоге получаем систему неравенств:<br> 1 <br> + _ <br> / 4 > ( <br> 0 1 / 4 X<br> <br>Рис. 228<br>281<br>х>0, 45-х>0, 45л:-л:2 <200.<br>Первые два неравенства можно записать в виде двойного неравенства 0 < х < 45. Решая третье неравенство системы, находим:<br>х2 -45х + 200>0; (х-40Хх~5)>0; ас<5; х>40 (рис.229).<br>Отметив на числовой прямой эти решения совместно с полученным ранее интервалом 0 < х <45, находим их пересечение (рис. 230), т.е. решение составленной выше системы неравенств: 0 < х < 5; 40 < х < 45.<br>Ответ:0<х<5; 40<х<45.<br> 1 1 1 1 <br> + + л <br> Л <br> ч У г 41 г» X<br> <br> I <br> <br> <br> о с 4 4 -0- И 5 X<br> 1 <br>Рис. 229 Рис. 230<br>Пример 4. Решить неравенство 1о§2 х2 -51о§2 х +1 <0. Решение. Здесь «напрашивается» введение новой переменной V = х, но сначала надо разобраться с выражением \о§22 х2.<br>Имеем: 1о§2 х2 =(1о§2 х2)? =(21ое2 х)? =41о§2 х. Итак, если у = х, то<br>х2 =4(/. Поняв это, перепишем заданное неравенство в виде<br>4^-бу+КО.<br>Найдем корни квадратного трехчлена 4у2 - 5у +1: у, = 1, у2 = —. Значит,<br>4<br>4 у2 -5у + 1=4(у-1) у — 1а потому последнее неравенство можно перепи-<br>I V<br>сать в виде 4(у -1) I у - — < 0.<br>Находим решение неравенства: -< у <1.<br>4<br>Подставив вместо у выражение 1о^2 х, получим: — < 1о§2 х <1 или, что то<br>4<br>же самое, 24 <1о^2 х <1ое2 2. Остается «освободиться» от знаков лога-рифмов, сохранив имеющиеся знаки неравенств: 24 < х <2. Ответ: 24 <х<2.
| + | • Во-вторых, решая логарифмическое неравенство, используя замену переменных, нам необходимо решать неравенства относительно замены до того момента, пока мы не получим простейшее неравенство.<br> |
| | | | |
| - | А.Г. Мордкович Алгебра 10 класс | + | Но это мы с вами рассмотрели сходные моменты решения логарифмических неравенств. А сейчас обратим внимание на довольно таки существенное отличие. Нам с вами известно, что логарифмическая функция обладает ограниченной областью определения, поэтому переходя от логарифмов к выражениям, стоящим под знаком логарифма, нужно брать в расчет область допустимых значений (ОДЗ). |
| | | | |
| | + | То есть, следует учитывать, что решая логарифмическое уравнение мы с вами, можем сначала находить корни уравнения, а потом делать проверку этого решения. А вот решить логарифмическое неравенство так не получится, поскольку переходя от логарифмов к выражениям, стоящим под знаком логарифма, необходимо будет записывать ОДЗ неравенства. |
| | + | |
| | + | Вдобавок стоит запомнить, что теория неравенств состоит из действительных чисел, которыми являются положительные и отрицательные числа, а также и число 0. |
| | + | |
| | + | Например, когда число «а» является положительным, то необходимо использовать такую запись: a >0. В этом случае, как сумма, так и произведение таких этих чисел также будут положительными. |
| | + | |
| | + | Основным принципом решения неравенства является его замена на более простое неравенство, но главное, чтобы оно было равносильно данному. Дальше, также мы получили неравенство и снова его заменили на то, которое имеет более простой вид и т.д. |
| | + | |
| | + | Решая неравенства с переменной нужно находить все его решения. Если два неравенства имеют одну переменную х, то такие неравенства равносильны, при условии, что их решения совпадают. |
| | + | |
| | + | Выполняя задания на решение логарифмических неравенств, необходимо запомнить, что когда a > 1, то логарифмическая функция возрастает, а когда 0 < a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить. |
| | + | |
| | + | <h2>Способы решения логарифмических неравенств</h2> |
| | + | |
| | + | Сейчас рассмотрим некоторые способы, которые имеют место при решении логарифмических неравенств. Для лучшего понимания и усвоения, попытаемся в них разобраться на конкретных примерах. |
| | + | |
| | + | Нам с вами известно, что простейшее логарифмическое неравенство имеет такой вид: |
| | + | |
| | + | <br> |
| | + | [[Image:10kl_LogNer01.jpg|200x200px|лог.неравенства]] |
| | + | <br> |
| | + | |
| | + | В этом неравенстве V – является одним из таких знаков неравенства, как: <,>, ≤ или ≥. |
| | + | |
| | + | Когда основание данного логарифма больше единицы (a>1), осуществляя переход от логарифмов к выражениям, стоящим под знаком логарифма, то в этом варианте знак неравенства сохраняется, и неравенство будет иметь такой вид: |
| | + | |
| | + | <br> |
| | + | [[Image:10kl_LogNer01.jpg|200x200px|лог.неравенства]] |
| | + | <br> |
| | + | |
| | + | что равносильно такой вот системе: |
| | + | |
| | + | <br> |
| | + | [[Image:10kl_LogNer02.jpg|200x200px|лог.неравенства]] |
| | + | <br> |
| | + | |
| | + | В случае же, когда основание логарифма больше нуля и меньше единицы (0<a<1), то в момент преображения от логарифмов к выражениям, которые стоят под знаком логарифма - знак неравенства будет изменен на противоположный, и неравенство приобретет такой вид: |
| | + | |
| | + | <br> |
| | + | [[Image:10kl_LogNer01.jpg|200x200px|лог.неравенства]] |
| | + | <br> |
| | + | |
| | + | Это равносильно данной системе: |
| | + | |
| | + | <br> |
| | + | [[Image:10kl_LogNer03.jpg|200x200px|лог.неравенства]] |
| | + | <br> |
| | + | |
| | + | Посмотрим еще примеры решения простейших логарифмических неравенств, приведенных на картинке ниже: |
| | + | |
| | + | <br> |
| | + | [[Image:10kl_LogNer04.jpg|500x500px|лог.неравенства]] |
| | <br> | | <br> |
| | | | |
| - | <sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub> | + | <h2>Решение примеров</h2> |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | '''Задание.''' Давайте попробуем решить такое вот неравенство: |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | [[Image:10kl_LogNer05.jpg|200x200px|лог.неравенства]] |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | |
| | | | |
| - | '''<u>Практика</u>'''
| + | Решение области допустимых значений. |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | [[Image:10kl_LogNer06.jpg|200x200px|лог.неравенства]] |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | |
| | | | |
| - | '''<u>Дополнения</u>'''
| + | Теперь попробуем умножить его правую часть на: |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | [[Image:10kl_LogNer07.jpg|100x100px|лог.неравенства]] |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| | | | |
| - | <u>Совершенствование учебников и уроков
| + | Смотрим, что у нас получится: |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | [[Image:10kl_LogNer08.jpg|300x200px|лог.неравенства]] |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | <br> |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| | | | |
| | + | Далее, следуя свойствам логарифмов, возьмем и внесем коэффициент –2, как степень подлогарифмического выражения и в итоге получим: |
| | + | |
| | + | <br> |
| | + | [[Image:10kl_LogNer09.jpg|300x300px|лог.неравенства]] |
| | + | <br> |
| | | | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | Теперь, давайте с вами перейдем к преобразованию подлогарифмических выражений. В связи с тем, что основание логарифма 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: |
| - | </u>
| + | |
| | | | |
| - | <br> | + | 3x - 8 > 16;<br> |
| | + | 3x > 24;<br> |
| | + | х > 8.<br> |
| | + | |
| | + | А из этого следует, что интервал, который мы получили, целиком и полностью принадлежит ОДЗ и является решением такого неравенства. |
| | + | |
| | + | Вот какой ответ у нас получился: |
| | + | |
| | + | <br> |
| | + | [[Image:10kl_LogNer10.jpg|150x150px|лог.неравенства]] |
| | + | <br> |
| | + | |
| | + | <h2>Что необходимо для решения логарифмических неравенств?</h2> |
| | + | |
| | + | А теперь давайте попробуем проанализировать, что нам необходимо для успешного решения логарифмических неравенств? |
| | + | |
| | + | • Во-первых, сосредоточить все свое внимание и постараться не допускать ошибок при выполнении преобразований, которые даны в этом неравенстве. Также, следует запомнить, что при решении таких неравенств нужно не допускать расширений и сужений ОДЗ неравенства, которые могут привести к потере или приобретению посторонних решений.<br> |
| | + | |
| | + | • Во-вторых, при решении логарифмических неравенств необходимо научиться мыслить логически и понимать разницу между такими понятиями, как система неравенств и совокупность неравенств, чтобы вы без проблем смогли осуществлять отбор решений неравенства, при этом руководствуясь его ОДЗ.<br> |
| | + | |
| | + | • В-третьих, для успешного решения таких неравенств каждый из вас должен отлично знать все свойства элементарных функций и четко понимать их смысл. К таким функциям относятся не только логарифмические, но и рациональные, степенные, тригонометрические и т.д., одним словом, все те, которые вы изучали на протяжении школьного обучения алгебры.<br> |
| | + | |
| | + | Как видите, изучив тему о логарифмических неравенствах, в решении этих неравенств нет ничего сложного при условии, если вы будете внимательны и настойчивы в достижении поставленных целей. Чтобы в решении неравенств не возникало никаких проблем, нужно как можно больше тренироваться, решая различные задания и при этом запоминать основные способы решения таких неравенств и их систем. При неудачных решениях логарифмических неравенств, следует внимательно проанализировать свои ошибки, чтобы в будущем не возвращаться к ним снова. |
| | + | |
| | + | <h2>Домашнее задание</h2> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | Для лучшего усвоения темы и закрепления пройденного материала, решите следующие неравенства: |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | <br> |
| | + | [[Image:10kl_LogNer11.jpg|300x300px|лог.неравенства]] |
| | + | <br> |
Текущая версия на 19:29, 26 августа 2015
Гипермаркет знаний>>Математика>>Математика 10 класс>> Логарифмические неравенства
Логарифмические неравенства
На предыдущих уроках мы с вами познакомились с логарифмическими уравнениями и теперь знаем, что это такое и как их решать. А сегодняшний урок будет посвящен изучению логарифмических неравенств. Что же это за такие неравенства и в чем разница между решением логарифмического уравнения и неравенства?
Логарифмические неравенства - это неравенства, которые имеют переменную, стоящую под знаком логарифма или в его основании.
Или же, можно еще сказать, что логарифмическое неравенство – это такое неравенство, в котором его неизвестная величина, как и в логарифмическом уравнении, будет стоять под знаком логарифма.
Простейшие логарифмические неравенства имеют такой вид:
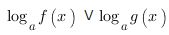
где f(x) и g(x) являются некоторыми выражениями, которые зависят от x.
Давайте это рассмотрим на таком примере: f(x)=1+2x+x2, g(x)=3x−1.
Решение логарифмических неравенств
Перед решением логарифмических неравенств, стоит отметить, что они при решении имеют сходство с показательными неравенствами, а именно:
• Во-первых, при переходе от логарифмов к выражениям, стоящим под знаком логарифма, нам также необходимо сравнить основание логарифма с единицей;
• Во-вторых, решая логарифмическое неравенство, используя замену переменных, нам необходимо решать неравенства относительно замены до того момента, пока мы не получим простейшее неравенство.
Но это мы с вами рассмотрели сходные моменты решения логарифмических неравенств. А сейчас обратим внимание на довольно таки существенное отличие. Нам с вами известно, что логарифмическая функция обладает ограниченной областью определения, поэтому переходя от логарифмов к выражениям, стоящим под знаком логарифма, нужно брать в расчет область допустимых значений (ОДЗ).
То есть, следует учитывать, что решая логарифмическое уравнение мы с вами, можем сначала находить корни уравнения, а потом делать проверку этого решения. А вот решить логарифмическое неравенство так не получится, поскольку переходя от логарифмов к выражениям, стоящим под знаком логарифма, необходимо будет записывать ОДЗ неравенства.
Вдобавок стоит запомнить, что теория неравенств состоит из действительных чисел, которыми являются положительные и отрицательные числа, а также и число 0.
Например, когда число «а» является положительным, то необходимо использовать такую запись: a >0. В этом случае, как сумма, так и произведение таких этих чисел также будут положительными.
Основным принципом решения неравенства является его замена на более простое неравенство, но главное, чтобы оно было равносильно данному. Дальше, также мы получили неравенство и снова его заменили на то, которое имеет более простой вид и т.д.
Решая неравенства с переменной нужно находить все его решения. Если два неравенства имеют одну переменную х, то такие неравенства равносильны, при условии, что их решения совпадают.
Выполняя задания на решение логарифмических неравенств, необходимо запомнить, что когда a > 1, то логарифмическая функция возрастает, а когда 0 < a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Способы решения логарифмических неравенств
Сейчас рассмотрим некоторые способы, которые имеют место при решении логарифмических неравенств. Для лучшего понимания и усвоения, попытаемся в них разобраться на конкретных примерах.
Нам с вами известно, что простейшее логарифмическое неравенство имеет такой вид:
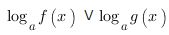
В этом неравенстве V – является одним из таких знаков неравенства, как: <,>, ≤ или ≥.
Когда основание данного логарифма больше единицы (a>1), осуществляя переход от логарифмов к выражениям, стоящим под знаком логарифма, то в этом варианте знак неравенства сохраняется, и неравенство будет иметь такой вид:
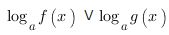
что равносильно такой вот системе:
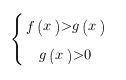
В случае же, когда основание логарифма больше нуля и меньше единицы (0<a<1), то в момент преображения от логарифмов к выражениям, которые стоят под знаком логарифма - знак неравенства будет изменен на противоположный, и неравенство приобретет такой вид:
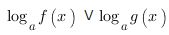
Это равносильно данной системе:
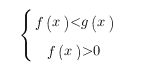
Посмотрим еще примеры решения простейших логарифмических неравенств, приведенных на картинке ниже:
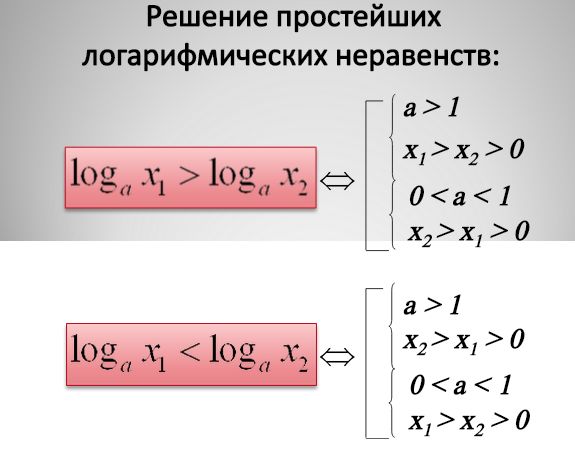
Решение примеров
Задание. Давайте попробуем решить такое вот неравенство:
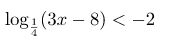
Решение области допустимых значений.
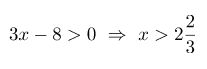
Теперь попробуем умножить его правую часть на:
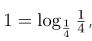
Смотрим, что у нас получится:
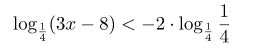
Далее, следуя свойствам логарифмов, возьмем и внесем коэффициент –2, как степень подлогарифмического выражения и в итоге получим:
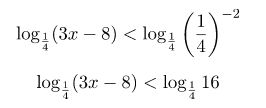
Теперь, давайте с вами перейдем к преобразованию подлогарифмических выражений. В связи с тем, что основание логарифма 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный:
3x - 8 > 16;
3x > 24;
х > 8.
А из этого следует, что интервал, который мы получили, целиком и полностью принадлежит ОДЗ и является решением такого неравенства.
Вот какой ответ у нас получился:
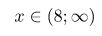
Что необходимо для решения логарифмических неравенств?
А теперь давайте попробуем проанализировать, что нам необходимо для успешного решения логарифмических неравенств?
• Во-первых, сосредоточить все свое внимание и постараться не допускать ошибок при выполнении преобразований, которые даны в этом неравенстве. Также, следует запомнить, что при решении таких неравенств нужно не допускать расширений и сужений ОДЗ неравенства, которые могут привести к потере или приобретению посторонних решений.
• Во-вторых, при решении логарифмических неравенств необходимо научиться мыслить логически и понимать разницу между такими понятиями, как система неравенств и совокупность неравенств, чтобы вы без проблем смогли осуществлять отбор решений неравенства, при этом руководствуясь его ОДЗ.
• В-третьих, для успешного решения таких неравенств каждый из вас должен отлично знать все свойства элементарных функций и четко понимать их смысл. К таким функциям относятся не только логарифмические, но и рациональные, степенные, тригонометрические и т.д., одним словом, все те, которые вы изучали на протяжении школьного обучения алгебры.
Как видите, изучив тему о логарифмических неравенствах, в решении этих неравенств нет ничего сложного при условии, если вы будете внимательны и настойчивы в достижении поставленных целей. Чтобы в решении неравенств не возникало никаких проблем, нужно как можно больше тренироваться, решая различные задания и при этом запоминать основные способы решения таких неравенств и их систем. При неудачных решениях логарифмических неравенств, следует внимательно проанализировать свои ошибки, чтобы в будущем не возвращаться к ним снова.
Домашнее задание
Для лучшего усвоения темы и закрепления пройденного материала, решите следующие неравенства:
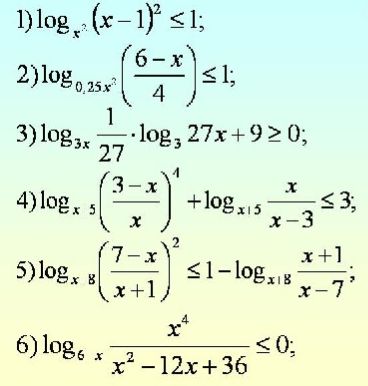
|