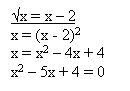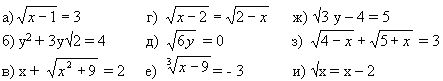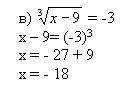|
|
|
| (5 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Иррациональные уравнения</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Иррациональные уравнения, математическая модель, иррационального, возведения, выражения, корни, квадрат, уравнение, отрицательное число, переменную, знаменателя</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Иррациональные уравнения''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Иррациональные уравнения''' |
| | | | |
| - | '''<br>'''
| + | <h2>Иррациональные уравнения</h2> |
| | | | |
| - | <br>
| + | Сегодняшний наш урок будет посвящен изучению уравнений, у которых переменная стоит под знаком квадратного или другого корня. Мы с вами попробуем на примерах уравнений подробно разобраться и научиться правильно решать иррациональные уравнения. |
| | | | |
| - | ''' ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ '''
| + | Естественно, в первую очередь нам необходимо выяснить, какие же уравнения являются иррациональными. Давайте для начала озвучим определение такого уравнения. |
| | | | |
| - | <br>Если в уравнении переменная содержится под знаком квадратного корня, то уравнение называют иррациональным. <br>Иногда математическая модель реальной ситуации представляет собой иррациональное уравнение, мы с этим уже встречались (см. замечание к примеру 3 из § 22). Поэтому нам следует научиться решать хотя бы простейшие иррациональные уравнения. <br>Рассмотрим иррациональное уравнение
| + | Уравнения называются иррациональными, если их переменная стоит под знаком корня. |
| | | | |
| - | [[Image:14-06-70.jpg]]<br><br>Это равенство, по определению квадратного корня, означает, что 2х + 1 = З2. Фактически от заданного иррационального уравнения мы перешли к рациональному уравнению 2х + 1 = 9, возведя в квадрат обе части иррационального уравнения. Метод возведения в квадрат обеих частей уравнения — основной метод решения иррациональных уравнений. Впрочем, это понятно: как же иначе освободиться от знака квадратного корня? Из уравнения 2х + 1 = 9 находим х = 4. <br>Это — и корень уравнения 2х + 1 = 9, и заданного иррационального уравнения. <br>Метод возведения в квадрат технически несложен, но иногда приводит к неприятностям. Рассмотрим, например, иррациональное уравнение
| + | А теперь давайте приведем примеры иррациональных уравнений и посмотрим, как они выглядят: |
| | | | |
| - | [[Image:14-06-71.jpg]]<br><br>Возведя обе его части в квадрат, получим | + | <br> |
| | + | [[Image:8kl_Irracion01.jpg|500x500px|иррац.числа]] |
| | + | <br> |
| | + | |
| | + | <h2>Как решаются иррациональные уравнения</h2> |
| | | | |
| - | [[Image:14-06-72.jpg]]<br><br>Далее имеем: <br>2x-4x = -7 +5; -2x = -2; х = 1. <br>Но значение х - 1, будучи корнем рационального уравнения 2x - 5 = 4x - 7, не является корнем заданного иррационального уравнения. Почему? Подставив 1 вместо х в заданное иррациональное уравнение, получим [[Image:14-06-73.jpg]] . Как же можно говорить о выполнении числового равенства, если и в левой и в правой его части содержатся выражения, не имеющие смысла? В подобных случаях говорят: х = 1 — посторонний корень для заданного иррационального уравнения. Получается, что заданное иррациональное уравнение не имеет корней. <br>Решим иррациональное уравнение
| + | Как правило, все иррациональные уравнения решаются в три этапа: |
| | | | |
| - | [[Image:14-06-74.jpg]]<br>-<br>Корни этого уравнения можно найти устно, как мы это делали в конце предыдущего параграфа: их произведение равно - 38, а сумма равна - 17; нетрудно догадаться, что это — числа 2 <br>и - 19. Итак, х<sub>1</sub> = 2, х<sub>2</sub> = - 19. <br>Подставив значение 2 вместо х в заданное иррациональное уравнение, получим
| + | • Во-первых, для начала необходимо уединить корень. Что это значит? То есть, если мы видим, что слева от знака равенства кроме корня есть еще и другие функции или числа, то в этом случае нам необходимо все это перенести вправо и поменять знак. Что же касается левой стороны, то здесь должен остаться лишь радикал и без всяких коэффициентов. |
| | | | |
| - | [[Image:14-06-75.jpg]]<br><br>Это неверно. <br>Подставив значение - 19 вместо х в заданное иррациональное уравнение, получим
| + | • Во-вторых, нам необходимо возвести в квадрат обе части этого уравнения. Но здесь не мешало бы быть внимательными и помнить, что к области значения корня относятся все неотрицательные числа. Из этого следует, что в иррациональном уравнении функция, которая расположена справа, также должна быть неотрицательной: g(x) ≥ 0. |
| | | | |
| - | [[Image:14-06-76.jpg]]<br><br>Это также неверно. <br>Каков же вывод? Оба найденные значения — посторонние корни. Иными словами, заданное иррациональное уравнение, как и предыдущее, не имеет корней. <br>Посторонний корень — не новое для вас понятие, посторонние корни уже встречались при решении рациональных уравнений, обнаружить их помогает проверка. Для иррациональных уравнений проверка — обязательный этап решения уравнения, который поможет обнаружить посторонние корни, если они есть, и отбросить их (обычно говорят «отсеять»).
| + | • В-третьих, и это будет логично, необходимо выполнить проверку. А такая необходимость может возникнуть потому, что на втором этапе при решении уравнения у нас могли появиться лишние корни. А чтобы от этих корней избавиться, нам нужно полученные числа-кандидаты взять и подставить в исходное уравнение. Ну, а потом, естественно, нужно проверить, получилось ли на самом деле верное числовое равенство. |
| | | | |
| - | Итак, иррациональное уравнение решают методом возведения обеих его частей в квадрат; решив полученное в итоге рациональное уравнение, надо обязательно сделать проверку, отсеяв возможные посторонние корни.
| + | <h2>Решение иррационального уравнения</h2> |
| | | | |
| - | Используя этот вывод, рассмотрим несколько примеров.
| + | А теперь, на приведенном примере, который был дан вначале нашего урока, попробуем разобраться с таким иррациональным уравнением. |
| | | | |
| - | '''Пример 1.''' Решить уравнение
| + | Посмотрев на это уравнение, мы видим, что в нем корень уже уединен, так как слева от знака равенства, кроме корня мы больше ничего не наблюдаем. |
| | | | |
| - | [[Image:14-06-77.jpg]]<br><br>Решение. Возведем обе части уравнения (1) в квадрат:
| + | Теперь давайте возведем обе стороны этого уравнения в квадрат и смотрим, что в итоге у нас получится: |
| | | | |
| - | [[Image:14-06-78.jpg]]<br>Далее последовательно имеем
| + | 2x2 − 14x + 13 = (5 − x)2<br> |
| | + | 2x2 − 14x + 13 = 25 − 10x + x2<br> |
| | + | x2 − 4x − 12 = 0<br> |
| | | | |
| - | 5х - 16 = х<sup>2</sup> - 4х + 4; <br>х<sup>2</sup> - 4х + 4 - 5х + 16 = 0; <br>х<sup>2</sup> - 9х + 20 = 0; <br>х<sub>1</sub> = 5, х<sub>2</sub> = 4. <br>Проверка. Подставив х = 5 в уравнение (1), получим [[Image:14-06-79.jpg]] — верное равенство. Подставив х = 4 в уравнение (1), получим [[Image:14-06-80.jpg]] — верное равенство. Значит, оба найденные значения — корни уравнения (1). <br>О т в е т: 4; 5.
| + | Теперь, через дискриминант попробуем решить квадратное уравнение, которое у нас получилось: |
| | | | |
| - | '''Пример 2.''' Решить уравнение [[Image:14-06-81.jpg]]<br>(это уравнение встретилось нам в § 22 и его решение мы «отложили до лучших времен»).иррационального уравнения, получим <br>2x2 + 8* + 16 = (44 - 2х)<sup>2</sup>. <br>Далее имеем <br>2х<sup>2</sup> + 8х + 16 = 1936 - 176x + 4x<sup>2</sup>; <br>- 2х<sup>2</sup> + 184x - 1920 = 0; <br>х<sup>2</sup> - 92x + 960 = 0; <br>х<sub>1 </sub>= 80, х<sup>2</sup> = 12. <br>Проверка. Подставив х = 80 в заданное иррациональное уравнение, получим
| + | D = b2 − 4ac = (−4)2 − 4 • 1 • (−12) = 16 + 48 = 64;<br> |
| | + | x1 = 6; x2 = −2<br> |
| | | | |
| - | [[Image:14-06-82.jpg]]<br><br>это, очевидно, неверное равенство, поскольку в его правой части содержится отрицательное число, а в левой — положительное число. Значит, х = 80 — посторонний корень для данного уравнения.
| + | Вот мы с вами решили уравнение и теперь нам нужно всего лишь в исходное уравнение подставить полученные числа и таким образом выполнить его проверку. |
| | | | |
| - | Подставив х = 12 в заданное иррациональное уравнение, получим
| + | Конечно же, можно поступить, еще более обдумано и итоговое решение, взять и упростить. |
| | | | |
| - | [[Image:14-06-83.jpg]]<br><br>т. е. .[[Image:14-06-84.jpg]] = 20, — верное равенство. Следовательно, х = 12 — корень данного уравнения. <br>Ответ: 12.
| + | <h2>Как упростить решение?</h2> |
| | | | |
| - | <br>
| + | А теперь давайте попробуем ответить на вопрос, зачем нам необходимо в конце решения иррационального уравнения делать проверку? На этот вопрос, естественно вы ответите, что проверка необходима для того, чтобы мы могли быть уверены в том, что при выполнении подстановки наших корней с правой стороны от знака равенства, стоит неотрицательное число. |
| | | | |
| - | [[Image:14-06-85.jpg]] <br>Разделим обе части последнего уравнения почленно на 2:
| + | Но ведь, нам и так известно, что в иррациональном уравнении арифметический квадратный корень уже по определению не может быть меньше нуля, поэтому число отрицательным также быть не может. |
| | | | |
| - | [[Image:14-06-86.jpg]]<br><br>Далее находим: <br>9 (x + 2) = 4 - 4х + х<sup>2</sup>; <br>9х + 18 - 4 + 4х - x<sup>2</sup> = 0; <br>- x<sup>2</sup> + 13x + 14 = 0; <br>x<sup>2</sup> - 13x - 14 = 0; <br>x<sub>1</sub> = 14, x<sub>2</sub> = -1. <br><br>Проверка. Подставив значение x = 14 в уравнение (2), получим [[Image:14-06-87.jpg]] — неверное равенство, значит, x = 14 — посторонний корень. <br>Подставив значение x = -1 в уравнение (2), получим <br>[[Image:14-06-88.jpg]] — верное равенство. Поэтому x = - 1 — корень уравнения (2). <br>О т в е т: - 1.
| + | Тогда возникает вопрос, что же, по сути, нам необходимо проверить? А все очень просто, нам нужно быть уверенными, что функция, которая стоит справа от знака равенства: |
| | | | |
| - | '''Пример 4.''' Решить уравнение <br>[[Image:14-06-89.jpg]]<br>Решение. Конечно, можно решить это уравнение по той же схеме, которую мы применяли в предыдущих примерах: переписать уравнение в виде
| + | g(x) = 5 − x, была, естественно, неотрицательной: |
| | | | |
| - | [[Image:14-06-90.jpg]] возвести обе части этого уравнения в квадрат, решить полученное рациональное уравнение и проверить найденные корни подстановкой их в <br>исходное иррациональное уравнение.
| + | g(x) ≥ 0 |
| | | | |
| - | Но мы применим более изящный способ: введем новую переменную у = фс . Тогда получим 2у2 + у - 3 = 0 — квадратное <br>уравнение относительно переменной у. Найдем его корни: у1 = 1, <br>3 <br>у2 = - -. Таким образом, задача свелась к решению двух <br>с* <br>уравнений: <br>3 <br>2" <br>Из первого уравнения находим х = 1, второе уравнение не <br>имеет корней (вы же помните, что у]х принимает только не- <br>отрицательные значения). <br>Ответ: 1. <br>Завершим этот параграф достаточно серьезным теоретиче- <br>ским разговором. Дело в следующем. Вы уже накопили некото- <br>рый опыт в решении различных уравнений: линейных, квадрат- <br>ных, рациональных, иррациональных. Вы знаете, что при ре- <br>шении уравнений выполняют различные преобразования, <br>например: <br>член уравнения переносят из одной части уравнения в дру- <br>гую с противоположным знаком; <br>обе части уравнения умножают или делят на одно и то же <br>отличное от нуля число; <br>освобождаются от знаменателя, т. е. заменяют уравнение <br>р(х) <br>= 0 уравнением р (х) = 0; <br>обе части уравнения возводят в квадрат. <br>Конечно, вы обратили внимание на то, что в результате <br>некоторых преобразований могли появиться посторонние кор- <br>ни, а потому приходилось быть бдительными: проверять все <br>найденные корни. Вот мы и попытаемся сейчас осмыслить все <br>это с теоретической точки зрения. <br>Определение. Два уравнения f (x) = g (x) и <br>r(x) = s (х) называют равносильными, если они <br>имеют одинаковые корни (или, в частности, <br>если оба уравнения не имеют корней). <br>Обычно при решении уравнения стараются <br>заменить данное уравнение более простым, но <br>равносильным ему. Такую замену называют рав- <br>носильным преобразованием уравнения. <br>Равносильными преобразованиями уравне- <br>ния являются следующие преобразования: <br>1. Перенос членов уравнения из одной части <br>уравнения в другую с противоположными <br>знаками. <br>Например, замена уравнения <br>2х + 5 = 7х - 8 <br>уравнением <br>2х - 7х = - 8 - 5 <br>есть равносильное преобразование уравнения. Это значит, что <br>уравнения 2х + 5 = 7х -8и 2х - 7х = -8-5 равносильны. <br>2. Умножение или деление обеих частей уравнения на одно и <br>то же отличное от нуля число. <br>Например, замена уравнения <br>0,5л;2 - 0,3* = 2 <br>уравнением <br>Ъх2 - Зх = 20 <br>(обе части уравнения умножили почленно на 10) есть равносиль- <br>ное преобразование уравнения. <br>Неравносильными преобразованиями уравне- <br>ния являются следующие преобразования: <br>1. Освобождение от знаменателей, содержащих <br>переменные. <br>Например, замена уравнения <br>„2 л <br>х-2 х-2 <br>уравнением х2 = 4 есть неравносильное преобразование урав- <br>нения. Дело в том, что уравнение хг = 4 имеет два корня: 2 и - <br>2, а заданному уравнению значение х = 2 удовлетворять не <br>может (знаменатель обращается в нуль). В подобных случаях <br>мы говорили так: х = 2 — посторонний корень. <br>2. Возведение обеих частей уравнения в квадрат. <br>Примеры приводить не будем, так как их было достаточно <br>много в этом параграфе. <br>Если в процессе решения уравнения применялось одно из <br>указанных неравносильных преобразований, то все найден- <br>ные корни надо проверить подстановкой в исходное уравне- <br>ние, поскольку среди них могут оказаться посторонние <br>корни. <br>11 Мордкович. Алгебра, учебник <br><br><br>
| + | С этим мы выяснили, теперь давайте подставим наши корни в эту функцию и получим такой результат: |
| | | | |
| - | <br> | + | g(x1) = g(6) = 5 − 6 = −1 < 0<br> |
| | + | g(x2) = g(−2) = 5 − (−2) = 5 + 2 = 7 > 0<br> |
| | | | |
| - | <sub>Полный перечень тем по классам, календарный план согласно школьной программе по математике [[Гипермаркет знаний - первый в мире!|онлайн]], видеоматериал по математике для 8 класса [[Математика|скачать]]</sub>
| + | И к какому мы выводу пришли? Подставив корни в функцию, мы видим, что корень x1 = 6 нам совершенно не подходит, так как, подставив его в правую часть исходного уравнения, у нас вышло отрицательное число. Тогда, когда корень x2 = −2 нас вполне устраивает, так как: |
| | | | |
| - | <br> | + | • Во-первых, потому, что этот корень и есть решением квадратного уравнения, так как был получен при помощи возведения в квадрат обеих сторон иррационального уравнения.<br> |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | • Во-вторых, потому, что при подстановке корня x2 = −2, в итоге, правая сторона исходного иррационального уравнения имеет положительное число. А так как это число положительно, то значит, что и область значений арифметического корня не нарушена.<br> |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | Вот мы с вами и решили алгоритм. Теперь вы видите, что, оказывается, решать уравнения с радикалами, не представляет никакой сложности. При решении таких уравнений во избежание вероятности получения лишних ответов, главное никогда не забывать делать проверку полученных корней.<br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | <h2>Исторические факты о иррациональных величинах</h2> |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | |
| - |
| + | А известно ли вам, что в переводе с латыни такое слово, как «иррациональный» звучит, как «неразумный». Но еще интересен тот факт, что параллельно с термином «неразумный» или «иррациональный» математики средневековья иррациональные числа еще нарекали термином «surdus», что в переводе звучало, как «глухой» и «немой». Складывается такое впечатление, что ученые не сильно жаловали иррациональные числа, считая их чем-то «неразумным», что нельзя ни высказать, ни выслушать. |
| - | '''<u>Практика</u>'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | Но, если поначалу математики Древнего мира практически отказывались воспринимать иррациональные числа, то со временем начали проявлять пристальное внимание к таким объектам математики. |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | А знаете ли вы, что в период бурного развития математических наук и астрономии математики Индии, Ближнего и Среднего Востока, длительное время отвергали иррациональные числа, хотя практически не могли обходиться без иррациональных величин. |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | А знаете ли вы, откуда появилось такое современное обозначение квадратного корня? Оказывается, начиная с тринадцатого века, длились эволюционные изменения знака радикала. Впервые название квадратному корню дали итальянские математики от латинского слова Radix, что в переводе обозначало корень, а его сокращенным вариантом была буква R. |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | |
| - |
| + | <h2>Домашнее задание</h2> |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | Изучив тему иррациональных уравнений, выполните домашнее задание, решив данные уравнения, и дайте ответы на поставленные вопросы. |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | 1. Решите данное уравнение: |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | <br> |
| - |
| + | [[Image:8kl_Irracion02.jpg|200x200px|иррац.числа]] |
| - | '''<u>Дополнения</u>'''
| + | <br> |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| - | '''<u></u>'''
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| | | | |
| - |
| + | Ответьте на вопросы: |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| | + | • Как вы думаете, будет ли это уравнение иррациональным?<br> |
| | + | • Какой у этого уравнения показатель корня? Он будет отрицательным или неотрицательным?<br> |
| | + | • Какая в этом случае будет формула?<br> |
| | + | • Как вы будете решать это уравнение?<br> |
| | + | |
| | + | 2. Решите данные уравнения и скажите, какие из них являются иррациональными? |
| | + | |
| | + | <br> |
| | + | [[Image:8kl_Irracion03.jpg|500x500px|иррац.числа]] |
| | <br> | | <br> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | 3. Решите уравнение: |
| | + | |
| | + | <br> |
| | + | [[Image:8kl_Irracion04.jpg|200x200px|иррац.числа]] |
| | + | <br> |
| | + | |
| | + | Дайте ответы на поставленные вопросы: |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | • Какое перед вами уравнение и является ли оно иррациональным?<br> |
| | + | • Какой показатель корня у этого уравнения?<br> |
| | + | • Как бы вы решали это уравнение?<br> |
| | + | • Сколько вы получили корней при решении этого уравнения?<br> |
| | + | • Нужна ли проверка этого уравнения?<br> |
| | + | • Каким методом можно воспользоваться, чтобы перейти от иррационального уравнения к рациональному?<br> |
| | + | • Существует ли вероятность появления постороннего корня в этом уравнении?<br> |
| | + | • Почему необходимо делать проверку корня?<br> |
| | + | • В каких случаях, при решении иррациональных уравнений проверка корней не требуется?<br> |
Текущая версия на 17:32, 3 сентября 2015
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Иррациональные уравнения
Иррациональные уравнения
Сегодняшний наш урок будет посвящен изучению уравнений, у которых переменная стоит под знаком квадратного или другого корня. Мы с вами попробуем на примерах уравнений подробно разобраться и научиться правильно решать иррациональные уравнения.
Естественно, в первую очередь нам необходимо выяснить, какие же уравнения являются иррациональными. Давайте для начала озвучим определение такого уравнения.
Уравнения называются иррациональными, если их переменная стоит под знаком корня.
А теперь давайте приведем примеры иррациональных уравнений и посмотрим, как они выглядят:

Как решаются иррациональные уравнения
Как правило, все иррациональные уравнения решаются в три этапа:
• Во-первых, для начала необходимо уединить корень. Что это значит? То есть, если мы видим, что слева от знака равенства кроме корня есть еще и другие функции или числа, то в этом случае нам необходимо все это перенести вправо и поменять знак. Что же касается левой стороны, то здесь должен остаться лишь радикал и без всяких коэффициентов.
• Во-вторых, нам необходимо возвести в квадрат обе части этого уравнения. Но здесь не мешало бы быть внимательными и помнить, что к области значения корня относятся все неотрицательные числа. Из этого следует, что в иррациональном уравнении функция, которая расположена справа, также должна быть неотрицательной: g(x) ≥ 0.
• В-третьих, и это будет логично, необходимо выполнить проверку. А такая необходимость может возникнуть потому, что на втором этапе при решении уравнения у нас могли появиться лишние корни. А чтобы от этих корней избавиться, нам нужно полученные числа-кандидаты взять и подставить в исходное уравнение. Ну, а потом, естественно, нужно проверить, получилось ли на самом деле верное числовое равенство.
Решение иррационального уравнения
А теперь, на приведенном примере, который был дан вначале нашего урока, попробуем разобраться с таким иррациональным уравнением.
Посмотрев на это уравнение, мы видим, что в нем корень уже уединен, так как слева от знака равенства, кроме корня мы больше ничего не наблюдаем.
Теперь давайте возведем обе стороны этого уравнения в квадрат и смотрим, что в итоге у нас получится:
2x2 − 14x + 13 = (5 − x)2
2x2 − 14x + 13 = 25 − 10x + x2
x2 − 4x − 12 = 0
Теперь, через дискриминант попробуем решить квадратное уравнение, которое у нас получилось:
D = b2 − 4ac = (−4)2 − 4 • 1 • (−12) = 16 + 48 = 64;
x1 = 6; x2 = −2
Вот мы с вами решили уравнение и теперь нам нужно всего лишь в исходное уравнение подставить полученные числа и таким образом выполнить его проверку.
Конечно же, можно поступить, еще более обдумано и итоговое решение, взять и упростить.
Как упростить решение?
А теперь давайте попробуем ответить на вопрос, зачем нам необходимо в конце решения иррационального уравнения делать проверку? На этот вопрос, естественно вы ответите, что проверка необходима для того, чтобы мы могли быть уверены в том, что при выполнении подстановки наших корней с правой стороны от знака равенства, стоит неотрицательное число.
Но ведь, нам и так известно, что в иррациональном уравнении арифметический квадратный корень уже по определению не может быть меньше нуля, поэтому число отрицательным также быть не может.
Тогда возникает вопрос, что же, по сути, нам необходимо проверить? А все очень просто, нам нужно быть уверенными, что функция, которая стоит справа от знака равенства:
g(x) = 5 − x, была, естественно, неотрицательной:
g(x) ≥ 0
С этим мы выяснили, теперь давайте подставим наши корни в эту функцию и получим такой результат:
g(x1) = g(6) = 5 − 6 = −1 < 0
g(x2) = g(−2) = 5 − (−2) = 5 + 2 = 7 > 0
И к какому мы выводу пришли? Подставив корни в функцию, мы видим, что корень x1 = 6 нам совершенно не подходит, так как, подставив его в правую часть исходного уравнения, у нас вышло отрицательное число. Тогда, когда корень x2 = −2 нас вполне устраивает, так как:
• Во-первых, потому, что этот корень и есть решением квадратного уравнения, так как был получен при помощи возведения в квадрат обеих сторон иррационального уравнения.
• Во-вторых, потому, что при подстановке корня x2 = −2, в итоге, правая сторона исходного иррационального уравнения имеет положительное число. А так как это число положительно, то значит, что и область значений арифметического корня не нарушена.
Вот мы с вами и решили алгоритм. Теперь вы видите, что, оказывается, решать уравнения с радикалами, не представляет никакой сложности. При решении таких уравнений во избежание вероятности получения лишних ответов, главное никогда не забывать делать проверку полученных корней.
Исторические факты о иррациональных величинах
А известно ли вам, что в переводе с латыни такое слово, как «иррациональный» звучит, как «неразумный». Но еще интересен тот факт, что параллельно с термином «неразумный» или «иррациональный» математики средневековья иррациональные числа еще нарекали термином «surdus», что в переводе звучало, как «глухой» и «немой». Складывается такое впечатление, что ученые не сильно жаловали иррациональные числа, считая их чем-то «неразумным», что нельзя ни высказать, ни выслушать.
Но, если поначалу математики Древнего мира практически отказывались воспринимать иррациональные числа, то со временем начали проявлять пристальное внимание к таким объектам математики.
А знаете ли вы, что в период бурного развития математических наук и астрономии математики Индии, Ближнего и Среднего Востока, длительное время отвергали иррациональные числа, хотя практически не могли обходиться без иррациональных величин.
А знаете ли вы, откуда появилось такое современное обозначение квадратного корня? Оказывается, начиная с тринадцатого века, длились эволюционные изменения знака радикала. Впервые название квадратному корню дали итальянские математики от латинского слова Radix, что в переводе обозначало корень, а его сокращенным вариантом была буква R.
Домашнее задание
Изучив тему иррациональных уравнений, выполните домашнее задание, решив данные уравнения, и дайте ответы на поставленные вопросы.
1. Решите данное уравнение:
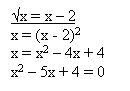
Ответьте на вопросы:
• Как вы думаете, будет ли это уравнение иррациональным?
• Какой у этого уравнения показатель корня? Он будет отрицательным или неотрицательным?
• Какая в этом случае будет формула?
• Как вы будете решать это уравнение?
2. Решите данные уравнения и скажите, какие из них являются иррациональными?
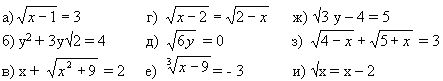
3. Решите уравнение:
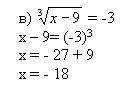
Дайте ответы на поставленные вопросы:
• Какое перед вами уравнение и является ли оно иррациональным?
• Какой показатель корня у этого уравнения?
• Как бы вы решали это уравнение?
• Сколько вы получили корней при решении этого уравнения?
• Нужна ли проверка этого уравнения?
• Каким методом можно воспользоваться, чтобы перейти от иррационального уравнения к рациональному?
• Существует ли вероятность появления постороннего корня в этом уравнении?
• Почему необходимо делать проверку корня?
• В каких случаях, при решении иррациональных уравнений проверка корней не требуется?
|