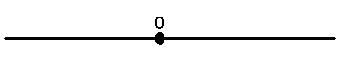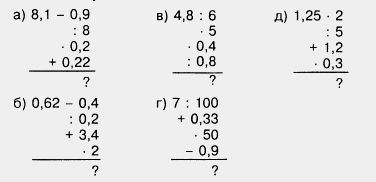|
|
|
| (2 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 5 класс, Алгебра, урок, на Тему, Угол, Прямой, развернутый угол, Чертежный треугольник</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 5 класс, Алгебра, урок, на Тему, Угол, Прямой, развернутый угол, Чертежный треугольник, точки, луча, треугольником, плоскость, прямоугольник, выражению</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Угол. Прямой и развернутый угол. Чертежный треугольник''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика: Угол. Прямой и развернутый угол. Чертежный треугольник''' |
| | | | |
| - | <br> | + | <h2>Что такое угол?</h2> |
| | | | |
| - | '''Угол. Прямой и развернутый угол. Чертежный треугольник '''
| + | Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160). <br>Лучи, образующие '''[[Кут. Вимірювання і побудова кутів. Транспортир. Види кугів. Бісектриса кута. Практикум|угол]]''', называют сторонами угла, а точку, из которой они выходят, — вершиной угла. <br>На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ. |
| | | | |
| - | <br>Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160). <br>Лучи, образующие '''угол''', называют '''сторонами''' угла, а точку, из которой они выходят, — '''вершиной''' угла. <br>На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ. <br>При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
| + | При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины. |
| | | | |
| - | Например, вместо «угол АОВ» пишут короче: «угол О». <br>Вместо слова «угол» пишут знак [[Image:18-06-1.jpg]]. <br>Например, [[Image:18-06-1.jpg]]AОВ, [[Image:18-06-1.jpg]]O. <br>На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и Улежат вне этого угла, а точки М и Н — на сторонах угла. | + | Например, вместо «угол АОВ» пишут короче: «угол О». |
| | | | |
| - | [[Image:18-06-2.jpg]]<br><br>Как и все геометрические фигуры, углы сравниваются с помощью наложения. <br>Если один угол можно наложить на другой так, что они совпадут, то эти углы равны. <br>Например, на рисунке 162 [[Image:18-06-1.jpg]]ABC = [[Image:18-06-1.jpg]]MNK.
| + | Вместо слова «угол» пишут знак [[Image:18-06-1.jpg]]. |
| | | | |
| - | [[Image:18-06-3.jpg]]<br>Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК. <br>Пишут: [[Image:18-06-1.jpg]]COP < [[Image:18-06-1.jpg]]COK и [[Image:18-06-1.jpg]]POK < [[Image:18-06-1.jpg]]COK. <br>Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164). <br>Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
| + | Например, [[Image:18-06-1.jpg]]AОВ, [[Image:18-06-1.jpg]]O. |
| | | | |
| - | [[Image:18-06-4.jpg]]<br><br>Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166). <br>Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми. <br>'''Прямым углом''' называют половину развернутого угла. | + | На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а '''[[Урок З. Точка. Прямая и кривая линии|точки]]''' М и Н — на сторонах угла. |
| | | | |
| - | [[Image:18-06-5.jpg]] | + | [[Image:18-06-2.jpg|180px|Угол]]<br><br>Как и все геометрические фигуры, углы сравниваются с помощью наложения. |
| | | | |
| | + | Если один угол можно наложить на другой так, что они совпадут, то эти углы равны. |
| | | | |
| | + | Например, на рисунке 162 [[Image:18-06-1.jpg]]ABC = [[Image:18-06-1.jpg]]MNK. |
| | | | |
| - | [[Image:18-06-6.jpg]]<br><br>Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо: <br>а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА; <br>б) провести вдоль второй стороны треугольника луч ОВ. | + | [[Image:18-06-3.jpg|480px|Угол.]] |
| | + | |
| | + | <br>Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК. |
| | + | |
| | + | Пишут: [[Image:18-06-1.jpg]]COP < [[Image:18-06-1.jpg]]COK и [[Image:18-06-1.jpg]]POK < [[Image:18-06-1.jpg]]COK. |
| | + | |
| | + | <h2>Прямой и развернутый угол</h2> |
| | + | |
| | + | Два дополнительных друг другу '''[[Плоскость. Прямая. Луч|луча]]''' образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164). |
| | + | |
| | + | Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165). |
| | + | |
| | + | [[Image:18-06-4.jpg|480px|Развернутый угол]]<br><br>Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166). |
| | + | |
| | + | Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми. |
| | + | |
| | + | Прямым углом называют половину развернутого угла. |
| | + | |
| | + | [[Image:18-06-5.jpg|320px|Задание]] |
| | + | |
| | + | <h2>Чертежный треугольник</h2> |
| | + | |
| | + | <br>[[Image:18-06-6.jpg|480px|Треугольник]]<br> |
| | + | |
| | + | Для построения прямого угла пользуются чертежным '''[[Задачі до теми Лічба в межах 20. Розв’язування задач на віднімання. Розпізнавання трикутників|треугольником]]''' (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо: |
| | + | |
| | + | а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА; |
| | + | |
| | + | б) провести вдоль второй стороны треугольника луч ОВ. |
| | | | |
| | В результате получим прямой угол АОВ. | | В результате получим прямой угол АОВ. |
| | | | |
| - | <br>'''Что такое угол? <br>Какой угол называют развернутым? <br>Какие углы называют равными?<br>Какой угол называют прямым?<br>Как строят прямой угол с помощью чертежного треугольника? '''
| + | '''Вопросы к теме''' |
| | + | |
| | + | 1.Что такое угол? <br> |
| | + | 2.Какой угол называют развернутым? <br> |
| | + | 3.Какие углы называют равными?<br> |
| | + | 4.Какой угол называют прямым?<br> |
| | + | 5.Как строят прямой угол с помощью чертежного треугольника?<br> |
| | + | |
| | + | <h2>Развернутый угол</h2> |
| | + | |
| | + | Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла. |
| | + | |
| | + | Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О. |
| | + | |
| | + | <br> |
| | + | [[Image:5kl_Razv.ygol01.jpg|500x500px|развернутый угол]] |
| | + | <br> |
| | + | |
| | + | Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных. |
| | + | |
| | + | Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла. |
| | + | |
| | + | А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым. |
| | + | |
| | + | <h2>Свойства развернутого угла</h2> |
| | + | |
| | + | Развернутый угол обладает такими свойствами: |
| | + | |
| | + | • во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;<br> |
| | + | • во-вторых, развернутый угол равен 180°;<br> |
| | + | • в-третьих, два смежных угла образуют развернутый угол;<br> |
| | + | • в-четвертых, развернутый угол составляет половину полного угла;<br> |
| | + | • в-пятых, полный угол будет равен сумме двух развёрнутых углов;<br> |
| | + | • в-шестых, половина развернутого угла составляет прямой угол.<br> |
| | + | |
| | + | <h2>Измерение углов</h2> |
| | + | |
| | + | Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам. |
| | + | |
| | + | То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: |
| | + | « ° ». |
| | + | |
| | + | Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным. |
| | + | |
| | + | А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360 : 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол. |
| | + | |
| | + | <h2>Практическое задание</h2> |
| | | | |
| - | <br>1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
| + | 1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения. |
| | | | |
| - | [[Image:18-06-7.jpg]]<br> | + | [[Image:18-06-7.jpg|480px|Уголы]]<br> |
| | | | |
| - | [[Image:18-06-8.jpg]] | + | [[Image:18-06-8.jpg|480px|Угол]] |
| | | | |
| - | 1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость? | + | 1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят '''[[Урок 12. Плоские поверхности. Плоскость|плоскость]]'''? |
| | | | |
| | 1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ? | | 1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ? |
| Строка 47: |
Строка 123: |
| | 1620. Укажите прямые углы в классной комнате. | | 1620. Укажите прямые углы в классной комнате. |
| | | | |
| - | 1621. Начертите прямоугольник со сторонами 6 см и 4 см и квадрат со стороной 7 см. | + | 1621. Начертите '''[[Акселеративна вправа до уроку на тему «Прямокутник. Задачі на знаходження третього додатка. Знаходження значень буквених виразів»|прямоугольник]]''' со сторонами 6 см и 4 см и квадрат со стороной 7 см. |
| | | | |
| - | [[Image:18-069.jpg]]<br><br>1622. С помощью чертежного треугольника начертите две прямые, которые при пересечении образуют прямые углы. На сколько частей они делят плоскость? Сколько развернутых углов на чертеже? | + | [[Image:18-069.jpg|480px|Угол. Прямой и развернутый угол]]<br><br>1622. С помощью чертежного треугольника начертите две прямые, которые при пересечении образуют прямые углы. На сколько частей они делят плоскость? Сколько развернутых углов на чертеже? |
| | | | |
| | 1623. Начертите круг с центром О и радиусом 4,5 см. Разделите круг на четыре доли и закрасьте [[Image:18-06-10.jpg]] круга. <br>1624. Вычислите устно: | | 1623. Начертите круг с центром О и радиусом 4,5 см. Разделите круг на четыре доли и закрасьте [[Image:18-06-10.jpg]] круга. <br>1624. Вычислите устно: |
| | | | |
| - | [[Image:18-06-11.jpg]]<br><br>1625. Уменьшится или увеличится число, если его: | + | [[Image:18-06-11.jpg|320px|Задание]]<br><br>1625. Уменьшится или увеличится число, если его: |
| | | | |
| | а) умножить на 2,5; 0,7; 0,01; 1,001; <br>б) разделить на 2,5; 0,7; 0,01; 1,001? | | а) умножить на 2,5; 0,7; 0,01; 1,001; <br>б) разделить на 2,5; 0,7; 0,01; 1,001? |
| Строка 65: |
Строка 141: |
| | 20; 40; 100; 0,1; 0,6; 1,5. | | 20; 40; 100; 0,1; 0,6; 1,5. |
| | | | |
| - | 1628. Составьте задачу по числовому выражению: | + | 1628. Составьте задачу по числовому '''[[Повторення таблиць додавання і віднімання. Складання виразів за текстовим формулюванням|выражению]]''': |
| | | | |
| | а) 0,09 • 200; б) 208 • 0,4; в) 130 • 0,1 + 80 • 0,1. | | а) 0,09 • 200; б) 208 • 0,4; в) 130 • 0,1 + 80 • 0,1. |
| Строка 77: |
Строка 153: |
| | 1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха? | | 1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха? |
| | | | |
| - | 1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для <br>Пети в начале учебного года? | + | 1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года? |
| | | | |
| | 1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди? | | 1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди? |
| | | | |
| - | 1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, <br>но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Алек- <br>сандрийского маяка. | + | 1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка. |
| | | | |
| | 1635. Найдите с помощью микрокалькулятора: | | 1635. Найдите с помощью микрокалькулятора: |
| Строка 89: |
Строка 165: |
| | 1636. Решите задачу: | | 1636. Решите задачу: |
| | | | |
| - | 1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать? <br>2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько <br>времени у него еще осталось? | + | 1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать? |
| | + | |
| | + | 2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось? |
| | | | |
| | 1637. Выполните действия: | | 1637. Выполните действия: |
| Строка 103: |
Строка 181: |
| | 1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь. | | 1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь. |
| | | | |
| - | [[Image:18-06-12.jpg]]<br><br>1642. Найдите значение выражения: | + | [[Image:18-06-12.jpg|480px|Задание]]<br><br>1642. Найдите значение выражения: |
| | | | |
| | а) 14,791 : а + 160,961 : b, если а = 100, b = 10; <br>б) 361,62с + 1848 : d, если с = 100, d =100. | | а) 14,791 : а + 160,961 : b, если а = 100, b = 10; <br>б) 361,62с + 1848 : d, если с = 100, d =100. |
| | | | |
| - | 1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день? | + | 1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил [http://xvatit.com/busines/jobs-career/ '''рабочий'''] во второй день? |
| | | | |
| | 1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке? | | 1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке? |
| Строка 117: |
Строка 195: |
| | а) 1% от тонны; в) 5% от 7 т; <br>б) 1% от литра; г) 6% от 80 км. | | а) 1% от тонны; в) 5% от 7 т; <br>б) 1% от литра; г) 6% от 80 км. |
| | | | |
| - | 1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна <br>0,9 т? | + | 1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т? |
| | | | |
| | 1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат? <br> | | 1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат? <br> |
| | | | |
| - | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> | + | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> |
| - | | + | |
| - | <sub>[[Гипермаркет знаний - первый в мире!|онлайн]] библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 5 класса [[Математика|скачать]]</sub>
| + | |
| - | | + | |
| - | <br>
| + | |
| - | | + | |
| - | '''<u>Содержание урока</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | |
| - |
| + | |
| - | '''<u>Практика</u>'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | |
| - |
| + | |
| - | '''<u>Дополнения</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| - | '''<u></u>'''
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| - | | + | |
| - | <br>
| + | |
| - | | + | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | |
| - | | + | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | |
Текущая версия на 15:09, 8 сентября 2015
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика: Угол. Прямой и развернутый угол. Чертежный треугольник
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол, называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак 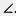 . .
Например, 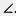 AОВ, AОВ, 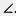 O. O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
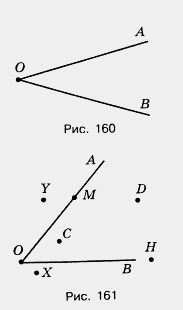
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 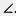 ABC = ABC = 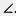 MNK. MNK.
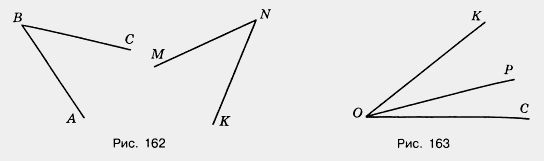
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: 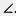 COP < COP < 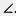 COK и COK и 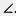 POK < POK < 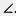 COK. COK.
Прямой и развернутый угол
Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
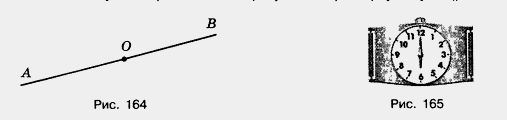
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.

Чертежный треугольник
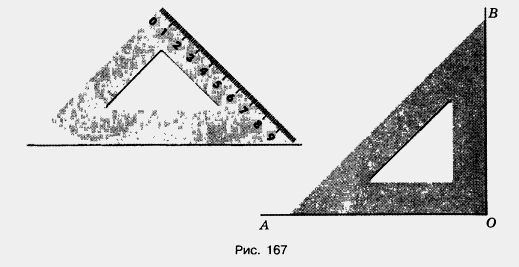
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Развернутый угол
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
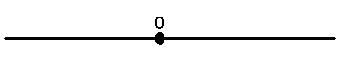
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
• во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
• во-вторых, развернутый угол равен 180°;
• в-третьих, два смежных угла образуют развернутый угол;
• в-четвертых, развернутый угол составляет половину полного угла;
• в-пятых, полный угол будет равен сумме двух развёрнутых углов;
• в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид:
« ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360 : 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
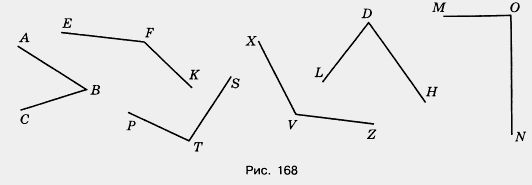
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость?
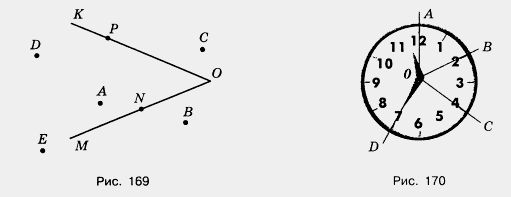
1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.
1620. Укажите прямые углы в классной комнате.
1621. Начертите прямоугольник со сторонами 6 см и 4 см и квадрат со стороной 7 см.
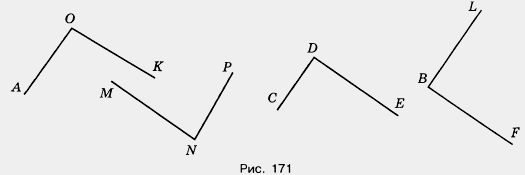
1622. С помощью чертежного треугольника начертите две прямые, которые при пересечении образуют прямые углы. На сколько частей они делят плоскость? Сколько развернутых углов на чертеже?
1623. Начертите круг с центром О и радиусом 4,5 см. Разделите круг на четыре доли и закрасьте 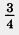 круга. круга.
1624. Вычислите устно:
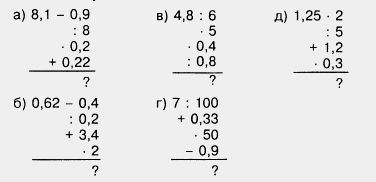
1625. Уменьшится или увеличится число, если его:
а) умножить на 2,5; 0,7; 0,01; 1,001;
б) разделить на 2,5; 0,7; 0,01; 1,001?
1626. Расскажите, как найти 7% числа а. Найдите:
а) 8% от 400; г) 25% от 28;
б) 30% от 20; д) 20% от 5.
в) 10% от 46;
1627. Найдите число, если 5% этого числа равны:
20; 40; 100; 0,1; 0,6; 1,5.
1628. Составьте задачу по числовому выражению:
а) 0,09 • 200; б) 208 • 0,4; в) 130 • 0,1 + 80 • 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79 : 7,8 - 6,8 : 17) • 3,04 - 2,04) • 0,85;
2) (3,42 : 0,57 • 9,5 - 6,6) : ((4,8 - 1,6) • (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
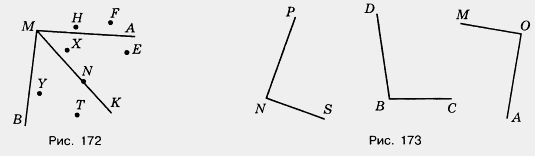
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК .Какая точка лежит внутри угла АМВ> но вне угла АМК .Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791 : а + 160,961 : b, если а = 100, b = 10;
б) 361,62с + 1848 : d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
|