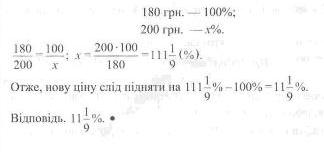|
|
|
| Строка 1: |
Строка 1: |
| - | '''[[Заглавная_страница|Гіпермаркет Знань]]>>[[Математика|Математика]]>>[[Математика 6 клас|Математика 6 клас]]>>Математика: Відсоткові розрахунки<metakeywords>математика 6 клас, 6 клас, урок на тему, урок, відсоткові розрахунки</metakeywords>''' | + | '''[[Заглавная страница|Гіпермаркет Знань]]>>[[Математика|Математика]]>>[[Математика 6 клас|Математика 6 клас]]>>Математика: Відсоткові розрахунки''' |
| | | | |
| - | <br> | + | <br> |
| | | | |
| - | Тут буде текст.
| + | Ми розв'язували задачі на відсотки зведенням їх до основних задач на дроби. Ці задачі можна розв'язувати і за допомогою пропорцій. Розглянемо такий спосіб розв'язування задач на відсотки.<br>Нехай у школі є 50 шестикласників. Тоді:<br>10% шестикласників — це 50 • 0,1 =5 (учнів); 20% шестикласників — це 50 • 0,2 = 10 (учнів); 40% шестикласників — це 50 • 0,4 = 20 (учнів). Яка існує залежність між числом відсотків і кількістю учнів, що відповідає цим відсоткам?<br>У скільки разів збільшується число відсотків, у стільки ж разів збільшу¬ється кількість учнів, що відповідає цим відсоткам.<br>Отже, число відсотків деякої величини прямо пропорційне значенню вели¬чини, що відповідає цим відсоткам.<br>Пам'ятаємо, що 100% деякої величини — це сама величина.<br> <br>Задача 1. Зі свіжих слив виходить 21% сушених. Скільки сушених слив можна отримати з 80 кг свіжих?<br>• Нехай з 80 кг свіжих слив можна отримати х кг сушених. Свіжі сливи становлять 100%, а сушені — 21%. Запишемо умову задачі у вигляді схеми:<br>80 кг — 100%;<br>хкг — 21%.<br>Яка залежність між масою син; та числом відсотків, що становить ия маса від маси свіжих слив?<br>Маса слив прямо пропорційна кількості відсотків, що становить ця маса від маси свіжих слив, тому:<br> <br>Відповідь. 16,8 кг. •<br>Задача 2. Банк дав підприємцеві кредит 10 000 грн. зі ставкою 7% річних. Яку суму повинен повернути підприємець банкові через півроку?<br>• Якщо відсоткова ставка за рік становить 7%, то за півроку буде нараховано 7% • 0,5 = 3,5% від початкової суми, тобто 10000 • 0,035 = 350 (грн.). Під¬приємець повинен повернути банку 10 000 + 350 = 10 350 (гри.).<br>Відповідь. 10 350 грн. • Задача 3. Фермер минулого року зібрав у середньому по ЗО ц зернових з 1 га, а в цьому році — по 32 ц. На скільки відсотків зросла урожайність зернових у цьому році порівняно з минулим роком?<br>• Спочатку знайдемо, на скільки центнерів більше зернових зібрав фер¬мер у цьому році: 32-30 = 2(ц). Тепер обчислимо, скільки відсотків становить знайдена різниця від урожаю минулого року. Оскільки порівнюємо з урожайніс¬тю минулого року,то 30 ц становить 100%, а 2 ц — х%. |
| | + | |
| | + | [[Image:asd195.jpg]]<br> |
| | + | |
| | + | 2) скільки відсотків становить одержана різниця від початкового зна¬чення величини.<br><br>Прочитайте<br><br>Задача 1. У процесі перегонки нафти з неї отримують 30% гасу. Скільки потрібно нафти, щоб одержати 9 т гасу?<br>• Маса нафти становить 100%, а маса гасу — 30%. Нехай щоб одержати 9 т гасу, потрібно переробити х т нафти. Запишемо умову задачі у вигляді схеми:<br>х т — 100%;<br>9т — 30%.<br>[[Image:asd196.jpg]]<br> |
| | + | |
| | + | Задача 3. Ціну на товар, що коштував 200 грн., знизили на 10%. На скільки відсотків потрібно підняти нову ціну, щоб отримати початкову?<br> |
| | + | |
| | + | [[Image:asd197.jpg]]<br> |
| | + | |
| | + | [[Image:asd198.jpg]]<br> |
| | + | |
| | + | Рівень А<br> <br> 737. Два трактори зорали поле площею 56 га, до того ж, перший трактор зорав 45% площі поля. Скільки гектарів зорав перший трактор?<br> <br> 738<br> <br> Трактор зорав 26 га, що становить 52% площі поля. Знайдіть площу поля.<br> <br> 739. Два трактори зорали поле площею 40 га, до того ж, перший трактор зорав 18 га. Скільки відсотків площі поля зорав перший трактор?<br> Знайдіть:<br> 740. а) 27% від числа 250; б) 72% від числа 1,25.<br> <br> 741: а) 64% від числа 7,5; б) 2,5% від числа 70<br> [[Image:asd199.jpg]]<br> |
| | + | |
| | + | 749.<br> <br> Робітник планував виготовити за зміну 20 деталей, однак перевиконав план на 5%. Скільки деталей виготовив робітник?<br> <br> 750. Вкладник вніс до банку 400 грн. під 15% річних. Яку суму грошей він матиме на рахунку через рік?<br> 751. Вкладник вніс до банку певну суму грошей під 17% річних і через рік одержав 819 грн. Яку суму вкладник вніс до банку?<br> <br> 752.<br> <br> Вкладник вніс до банку 500 грн. і через рік після нарахування річних від¬сотків мав на рахунку на 80 грн. більше. Скільки річних відсотків нарахо¬вував банк?<br> <br> 753. Узимку куртка коштувала 160 грн. Навесні ціну на неї знизили на 15%. Яка ціна куртки навесні?<br> <br> 7547<br> <br> У зв'язку з інфляцією ціна на масло протягом півроку виросла на 6%. Початкова ціна 1 кг масла становила 9 грн. 50 к. Якою стала ціна 1 кг ма¬сла через півроку?<br> <br> 755. Оператор набирає на комп'ютері за шестигодинний робочий день 30 сто¬рінок тексту. Скільки сторінок він набиратиме протягом години, якщо його продуктивність праці виросте на 20%?<br> 756. Підприємець отримав за місяць 16 000 грн. прибутку, з яких 7000 грн. витратив на розширення виробництва. Скільки відсотків отриманого при¬бутку підприємець витратив на розширення виробництва?<br> <br> 757. Перший учень стрибнув у довжину на 2,4 м, а стрибок другого був на 15% довший. Чому дорівнює довжина стрибка другого учня?<br> <br> |
| | + | |
| | + | [[Image:asd200.jpg]]<br> |
| | + | |
| | + | <br> |
| | + | |
| | + | 758. У серпні пакет акцій фірми коштував 4000 грн., а в жовтні — 4200 грн. На скільки відсотків зросла вартість пакету акцій фірми?<br> 759. На присадибній ділянці 50 м2 засаджено полуницями, а 40 м2 — помідо¬рами. На скільки відсотків площа під полуницями більша від площі під помідорами?<br> 760. У місті /V проїзд у маршрутному таксі коштує 1 грн., а в автобусі — 80 к. На скільки відсотків вартість проїзду в маршрутному таксі більша від вартості проїзду в автобусі?<br> <br> 761. Робітник за зміну виготовив 80 деталей, а його учень — 56. На скільки відсотків менше деталей виготовив учень, ніж робітник?<br> <br> 762. Довжина поля дорівнює 80 м, а ширина — 20 м. На скільки відсотків довжина поля більша від ширини? На скільки відсотків ширина поля менша від довжини?<br> <br> <br> Рівень Б<br> <br> 763. З 1,6 га землі, що становить 8% площі всього поля, зібрали 48 ц пшениці. Скільки центнерів пшениці зібрали з поля, якщо врожайність на усьому полі однакова?<br> <br> 764. Периметр трикутника дорівнює 36 см. Довжина першої сторони стано¬вить 25% периметра і 75% довжини другої сторони. Знайдіть довжину кожної сторони трикутника.<br> <br> 765. Фермер засіяв соняшником 1,8 га поля, що на 20% більше, ніж торік. Яку площу фермер засівав соняшником торік?<br> 766. Відстань між будинками Вінні-Пуха та П'ятачка становить 2 км. Одного дня Вінні-Пух пішов відвідати П'ятачка і витратив на дорогу 25 хв, а на¬ступного дня П'ятачок пішов відвідати Вінні-Пуха і витратив на дорогу 20 хв. Чия швидкість з них більша і на скільки відсотків?<br> <br> 767.<br> <br> Відстань між будинками Вінні-Пуха та П'ятачка дорівнює 2 км. П'ятачок за хвилину проходить 75 м, а Вінні-Пух — 50 м. Вони вирішили обміня¬тися подарунками і вийшли одночасно назустріч один одному. Хто з них пройде більшу відстань до зустрічі та на скільки відсотків?<br> <br> 768.<br> <br> Гроші в сумі 14 000 гри., зібрані на благодійному концерті, були розподі¬лені так: 45% грошей виділили для будинку дітей-сиріт, 42,5% — для бу¬динку престарілих, а на решту коштів купили піаніно для музикальної школи. Скільки коштує піаніно?<br> <br> 769. Три робітники виготовили замовлену партію деталей. Перший і другий робітники виготовили відповідно 30% і 40% усіх деталей, а третій — на 8 деталей менше, ніж другий. Скільки всього деталей виготовили робітники?<br> 770. Щоб урахувати інфляцію 4%, виробник холодильників підняв ціну на кожний холодильник з 1250 грн. до 1290 грн. Чи правильно він виконав розрахунки?<br> 771. Вкладник вніс до банку 500 грн. під 14% річних, через рік річна ставка зросла до 17%. Яку суму грошей він матиме на рахунку через 2 роки?<br> <br> 772. Банк дав підприємцеві кредит 20 000 грн. на 9 місяців зі ставкою 8% річ¬них. Яку суму підприємець повинен повернути через 9 місяців?<br> <br> <br> <br> 779. Ціну на товар, що коштував 150 грн., спочатку збільшили на 20%, а потім нову ціну зменшили на 20%. Знайдіть ціну товару після двох переоцінок.<br> <br> 780. Ціну на товар, що коштував 100 грн., зменшили на 20%. На скільки відсот¬ків потрібно підняти нову ціну, щоб отримати початкову?<br> 781. Сплав міді з оловом масою 12 кг містить 45% міді. Скільки кілограмів чистого олова потрібно додати до сплаву, щоб одержати новий сплав, який містив би 40% мілі?<br> <br> 782. У воді розчинили 180 г солі й одержали 12%-й розчин солі. Скільки гра¬мів води використали для приготування розчину?<br> <br> 783. Ціну на товар знизили на 20%. На скільки відсотків потрібно підвищити нову ціну, щоб отримати початкову?<br> 784. С два числа. Перше число на 20% більше від другого. У скільки разів пер¬ше число більше від другого? Знайдіть ці числа, якщо їх сума дорівнює 11.<br> <br> Здогадайтеся<br> <br> 785. На купівлю порції морозива Сергієві не вистачає 46 к., а Андрію — 5 к. Коли вони разом склали свої гроші, то їх усе ж не вистачило на морозиво — бракувало 1 копійки. Скільки коштує порція морозива?<br> <br> |
| | + | |
| | + | [[Image:asd201.jpg]]<br> |
| | + | |
| | + | 790. Знайдіть відношення:<br> а) 17 до 2; б) 10 до 3; в) 5 до 30.<br> <br> |
| | | | |
| | <br> <sub>шкільний [[Гіпермаркет Знань - перший в світі!|календарний план]], найбільша [[Математика|бібліотека рефератів]] з усіх предметів, [[Математика 6 клас|домашнє завдання]] з математики </sub><br> | | <br> <sub>шкільний [[Гіпермаркет Знань - перший в світі!|календарний план]], найбільша [[Математика|бібліотека рефератів]] з усіх предметів, [[Математика 6 клас|домашнє завдання]] з математики </sub><br> |
Версия 23:24, 14 марта 2010
Гіпермаркет Знань>>Математика>>Математика 6 клас>>Математика: Відсоткові розрахунки
Ми розв'язували задачі на відсотки зведенням їх до основних задач на дроби. Ці задачі можна розв'язувати і за допомогою пропорцій. Розглянемо такий спосіб розв'язування задач на відсотки.
Нехай у школі є 50 шестикласників. Тоді:
10% шестикласників — це 50 • 0,1 =5 (учнів); 20% шестикласників — це 50 • 0,2 = 10 (учнів); 40% шестикласників — це 50 • 0,4 = 20 (учнів). Яка існує залежність між числом відсотків і кількістю учнів, що відповідає цим відсоткам?
У скільки разів збільшується число відсотків, у стільки ж разів збільшу¬ється кількість учнів, що відповідає цим відсоткам.
Отже, число відсотків деякої величини прямо пропорційне значенню вели¬чини, що відповідає цим відсоткам.
Пам'ятаємо, що 100% деякої величини — це сама величина.
Задача 1. Зі свіжих слив виходить 21% сушених. Скільки сушених слив можна отримати з 80 кг свіжих?
• Нехай з 80 кг свіжих слив можна отримати х кг сушених. Свіжі сливи становлять 100%, а сушені — 21%. Запишемо умову задачі у вигляді схеми:
80 кг — 100%;
хкг — 21%.
Яка залежність між масою син; та числом відсотків, що становить ия маса від маси свіжих слив?
Маса слив прямо пропорційна кількості відсотків, що становить ця маса від маси свіжих слив, тому:
Відповідь. 16,8 кг. •
Задача 2. Банк дав підприємцеві кредит 10 000 грн. зі ставкою 7% річних. Яку суму повинен повернути підприємець банкові через півроку?
• Якщо відсоткова ставка за рік становить 7%, то за півроку буде нараховано 7% • 0,5 = 3,5% від початкової суми, тобто 10000 • 0,035 = 350 (грн.). Під¬приємець повинен повернути банку 10 000 + 350 = 10 350 (гри.).
Відповідь. 10 350 грн. • Задача 3. Фермер минулого року зібрав у середньому по ЗО ц зернових з 1 га, а в цьому році — по 32 ц. На скільки відсотків зросла урожайність зернових у цьому році порівняно з минулим роком?
• Спочатку знайдемо, на скільки центнерів більше зернових зібрав фер¬мер у цьому році: 32-30 = 2(ц). Тепер обчислимо, скільки відсотків становить знайдена різниця від урожаю минулого року. Оскільки порівнюємо з урожайніс¬тю минулого року,то 30 ц становить 100%, а 2 ц — х%.

2) скільки відсотків становить одержана різниця від початкового зна¬чення величини.
Прочитайте
Задача 1. У процесі перегонки нафти з неї отримують 30% гасу. Скільки потрібно нафти, щоб одержати 9 т гасу?
• Маса нафти становить 100%, а маса гасу — 30%. Нехай щоб одержати 9 т гасу, потрібно переробити х т нафти. Запишемо умову задачі у вигляді схеми:
х т — 100%;
9т — 30%.

Задача 3. Ціну на товар, що коштував 200 грн., знизили на 10%. На скільки відсотків потрібно підняти нову ціну, щоб отримати початкову?

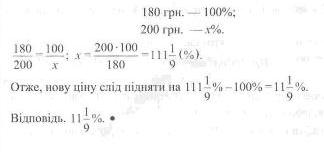
Рівень А
737. Два трактори зорали поле площею 56 га, до того ж, перший трактор зорав 45% площі поля. Скільки гектарів зорав перший трактор?
738
Трактор зорав 26 га, що становить 52% площі поля. Знайдіть площу поля.
739. Два трактори зорали поле площею 40 га, до того ж, перший трактор зорав 18 га. Скільки відсотків площі поля зорав перший трактор?
Знайдіть:
740. а) 27% від числа 250; б) 72% від числа 1,25.
741: а) 64% від числа 7,5; б) 2,5% від числа 70

749.
Робітник планував виготовити за зміну 20 деталей, однак перевиконав план на 5%. Скільки деталей виготовив робітник?
750. Вкладник вніс до банку 400 грн. під 15% річних. Яку суму грошей він матиме на рахунку через рік?
751. Вкладник вніс до банку певну суму грошей під 17% річних і через рік одержав 819 грн. Яку суму вкладник вніс до банку?
752.
Вкладник вніс до банку 500 грн. і через рік після нарахування річних від¬сотків мав на рахунку на 80 грн. більше. Скільки річних відсотків нарахо¬вував банк?
753. Узимку куртка коштувала 160 грн. Навесні ціну на неї знизили на 15%. Яка ціна куртки навесні?
7547
У зв'язку з інфляцією ціна на масло протягом півроку виросла на 6%. Початкова ціна 1 кг масла становила 9 грн. 50 к. Якою стала ціна 1 кг ма¬сла через півроку?
755. Оператор набирає на комп'ютері за шестигодинний робочий день 30 сто¬рінок тексту. Скільки сторінок він набиратиме протягом години, якщо його продуктивність праці виросте на 20%?
756. Підприємець отримав за місяць 16 000 грн. прибутку, з яких 7000 грн. витратив на розширення виробництва. Скільки відсотків отриманого при¬бутку підприємець витратив на розширення виробництва?
757. Перший учень стрибнув у довжину на 2,4 м, а стрибок другого був на 15% довший. Чому дорівнює довжина стрибка другого учня?

758. У серпні пакет акцій фірми коштував 4000 грн., а в жовтні — 4200 грн. На скільки відсотків зросла вартість пакету акцій фірми?
759. На присадибній ділянці 50 м2 засаджено полуницями, а 40 м2 — помідо¬рами. На скільки відсотків площа під полуницями більша від площі під помідорами?
760. У місті /V проїзд у маршрутному таксі коштує 1 грн., а в автобусі — 80 к. На скільки відсотків вартість проїзду в маршрутному таксі більша від вартості проїзду в автобусі?
761. Робітник за зміну виготовив 80 деталей, а його учень — 56. На скільки відсотків менше деталей виготовив учень, ніж робітник?
762. Довжина поля дорівнює 80 м, а ширина — 20 м. На скільки відсотків довжина поля більша від ширини? На скільки відсотків ширина поля менша від довжини?
Рівень Б
763. З 1,6 га землі, що становить 8% площі всього поля, зібрали 48 ц пшениці. Скільки центнерів пшениці зібрали з поля, якщо врожайність на усьому полі однакова?
764. Периметр трикутника дорівнює 36 см. Довжина першої сторони стано¬вить 25% периметра і 75% довжини другої сторони. Знайдіть довжину кожної сторони трикутника.
765. Фермер засіяв соняшником 1,8 га поля, що на 20% більше, ніж торік. Яку площу фермер засівав соняшником торік?
766. Відстань між будинками Вінні-Пуха та П'ятачка становить 2 км. Одного дня Вінні-Пух пішов відвідати П'ятачка і витратив на дорогу 25 хв, а на¬ступного дня П'ятачок пішов відвідати Вінні-Пуха і витратив на дорогу 20 хв. Чия швидкість з них більша і на скільки відсотків?
767.
Відстань між будинками Вінні-Пуха та П'ятачка дорівнює 2 км. П'ятачок за хвилину проходить 75 м, а Вінні-Пух — 50 м. Вони вирішили обміня¬тися подарунками і вийшли одночасно назустріч один одному. Хто з них пройде більшу відстань до зустрічі та на скільки відсотків?
768.
Гроші в сумі 14 000 гри., зібрані на благодійному концерті, були розподі¬лені так: 45% грошей виділили для будинку дітей-сиріт, 42,5% — для бу¬динку престарілих, а на решту коштів купили піаніно для музикальної школи. Скільки коштує піаніно?
769. Три робітники виготовили замовлену партію деталей. Перший і другий робітники виготовили відповідно 30% і 40% усіх деталей, а третій — на 8 деталей менше, ніж другий. Скільки всього деталей виготовили робітники?
770. Щоб урахувати інфляцію 4%, виробник холодильників підняв ціну на кожний холодильник з 1250 грн. до 1290 грн. Чи правильно він виконав розрахунки?
771. Вкладник вніс до банку 500 грн. під 14% річних, через рік річна ставка зросла до 17%. Яку суму грошей він матиме на рахунку через 2 роки?
772. Банк дав підприємцеві кредит 20 000 грн. на 9 місяців зі ставкою 8% річ¬них. Яку суму підприємець повинен повернути через 9 місяців?
779. Ціну на товар, що коштував 150 грн., спочатку збільшили на 20%, а потім нову ціну зменшили на 20%. Знайдіть ціну товару після двох переоцінок.
780. Ціну на товар, що коштував 100 грн., зменшили на 20%. На скільки відсот¬ків потрібно підняти нову ціну, щоб отримати початкову?
781. Сплав міді з оловом масою 12 кг містить 45% міді. Скільки кілограмів чистого олова потрібно додати до сплаву, щоб одержати новий сплав, який містив би 40% мілі?
782. У воді розчинили 180 г солі й одержали 12%-й розчин солі. Скільки гра¬мів води використали для приготування розчину?
783. Ціну на товар знизили на 20%. На скільки відсотків потрібно підвищити нову ціну, щоб отримати початкову?
784. С два числа. Перше число на 20% більше від другого. У скільки разів пер¬ше число більше від другого? Знайдіть ці числа, якщо їх сума дорівнює 11.
Здогадайтеся
785. На купівлю порції морозива Сергієві не вистачає 46 к., а Андрію — 5 к. Коли вони разом склали свої гроші, то їх усе ж не вистачило на морозиво — бракувало 1 копійки. Скільки коштує порція морозива?

790. Знайдіть відношення:
а) 17 до 2; б) 10 до 3; в) 5 до 30.
шкільний календарний план, найбільша бібліотека рефератів з усіх предметів, домашнє завдання з математики
Зміст уроку
 конспект уроку і опорний каркас конспект уроку і опорний каркас
 презентація уроку презентація уроку
 акселеративні методи та інтерактивні технології акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями) закриті вправи (тільки для використання вчителями)
 оцінювання
Практика оцінювання
Практика
 задачі та вправи,самоперевірка задачі та вправи,самоперевірка
 практикуми, лабораторні, кейси практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання
Ілюстрації домашнє завдання
Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати реферати
 фішки для допитливих фішки для допитливих
 шпаргалки шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення
 зовнішнє незалежне тестування (ЗНТ) зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні підручники основні і допоміжні
 тематичні свята, девізи тематичні свята, девізи
 статті статті
 національні особливості національні особливості
 словник термінів словник термінів
 інше
Тільки для вчителів інше
Тільки для вчителів
 ідеальні уроки ідеальні уроки
 календарний план на рік календарний план на рік
 методичні рекомендації методичні рекомендації
 програми програми
 обговорення обговорення
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|