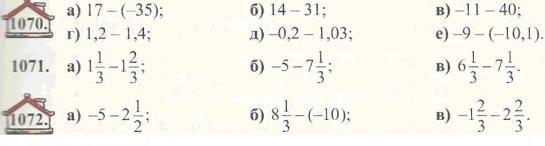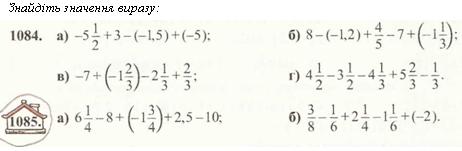|
|
|
| Строка 1: |
Строка 1: |
| - | '''[[Заглавная_страница|Гіпермаркет Знань]]>>[[Математика|Математика]]>>[[Математика 6 клас|Математика 6 клас]]>>Віднімання раціональних чисел<metakeywords>математика, 6 клас, клас, урок, на тему, віднімання раціональних чисел</metakeywords>''' | + | '''[[Заглавная страница|Гіпермаркет Знань]]>>[[Математика|Математика]]>>[[Математика 6 клас|Математика 6 клас]]>>Віднімання раціональних чисел''' |
| | | | |
| - | <br> | + | <br> |
| | | | |
| - | Тут туде текст.<br> <br> <sub>[[Гіпермаркет Знань - перший в світі!|Календарно-тематичне планування]] математики, [[Математика 6 клас|завдання школяру]] 6 класу, [[Математика|курси учителю]] математики </sub>
| + | Віднімання від'ємних чисел і чисел з різними знаками має такий самий зміст, що й віднімання додатних чисел. Нагадаємо, що за допомогою віднімання знаходять невідомий доданок за відомими сумою й одним з доданків.<br>Розглянемо приклади.<br>Оскільки -7 + (-8) = -15, то -15 - (-8) = -7.<br>Такий же результат одержимо, якщо до числа -15 додамо число, протилежне числу -8, тобто число +8. Тому різницю -15 - (-8) можна замінити сумою -15 + (+8), у якій до зменшуваного додається число, протилежне від'ємнику: -15-(-8) = -15+ (+8) = -7.<br><br>Отже, щоб від одного числа відняти інше, досить до зменшуваного додати число, протилежне від'ємнику.<br> <br>Це правило віднімання можна записати так:<br>а - Ь = а + (-Ь),<br>де а і Ь — будь-які раціональні числа. Зокрема, а - а = а + (-а) = 0.<br>Оскільки віднімання можна замінити додаванням протилежного числа, то будь-який вираз, який містить дії додавання і віднімання, можна записати як суму.<br>Наприклад, вираз -10 - (+7) є різницею чисел -10 і +7, його можна записати як суму чисел -10 і -7, бо -10 - (+7) = -10 + (-7). Правильно й навпаки: суму чисел -10 і -7 можна записати як різницю чисел -10 і 7, тобто -10 + (-7) -= -10-(+7).<br>Домовимося надалі додатні числа писати без знака «+», тобто суму -10 + (+7) записуватимемо так: -10 + 7, а різницю 14 - (+18) так: 14 - 18.<br>Нехай на координатній прямій задано дві точки А(-2) і В(5) (рис. 49) і потрібно знайти довжину відрізка АВ.<br>Щоб знайти довжину відрізка АВ (або відстань АВ), потрібно дізнатися, скільки одиничних відрізків містить цей відрізок. Як видно з рисунка, довжина відрізка АВ дорівнює 7 одиничним відрізкам. Через координати кінців відрізка АВ його довжина виражається так:<br>АВ = 5- (-2) = 7.<br>[[Image:asd293.jpg]] |
| | + | |
| | + | Отже, щоб знайти довжину відрізка на координатній прямій, потрібно від координати його правого кінця відняти координату лівого кінця.<br><br>Для тих, хто хоче знати більше<br><br>Якби при відшуканні довжини відрізка АВ (рис. 49) від координати лівого кінця відняли координату правого, то одержали б число -2 - 5 = -7. Довжина відрізка АВ є додатною величиною і в цьому випадку вона дорівнює модулю знайденого числа:<br>Л£ = |-2-5| = |-7| = 7.<br>Отже, довжина відрізка АВ дорівнює модулю різниці координат його лівого і правого кінців. Ця довжина також дорівнює модулю різниці координат правого і лівого кінців:<br>ЛЯ = |5-(-2)| = |5 + 2| = |7| = 7. Довжина відрізка дорівнює модулю різниці координат його кінців.<br> <br>Довжину відрізка АВ з кінцями А(х) і В(у) можна обчислити за формулою: АВ = \х-у\, або АВ = \у-х\.<br><br>Прочитайте<br><br>1. Обчислити:-18+15-(-11)-32.<br>• Запишемо вираз у вигляді суми і згрупуємо числа: -18+ 15-(-11)-32 = -18+ 15 + 11 +(-32) =<br>= (-18 + (-32)) + (15 + 11) = -50 + 26 = -24. •<br>2. Спростити вираз: -7 + а+8-а-(-11).<br>• Запишемо вираз у вигляді суми і згрупуємо доданки: -7 + а + 8-а-(-11) = -7 + <з + 8 + (-а)+11 =<br>= (-7 + 8 + 11) + (а + (-а))=12 + 0=12. •<br>3. Розв'язати рівняння: а)х + 10-27 = 13; б)|х + 5| = 2.<br>• а) Спочатку спростимо вираз у лівій частині рівняння:<br>х+ 10-27 = х+ 10 + (-27) = х + (-17) = х- 17.<br>Одержимо рівняння х- 17 = 13, звідки: х = 13 + 17; х = 30.<br>б) Якщо модуль числа дорівнює 2, то цим числом є 2 або -2, тому<br>х + 5 = 2 або х + 5 = -2. Розв'яжемо кожне із цих рівнянь.<br>х + 5 = 2; х + 5 = -2;<br>х 2 5, х 2 5 у<br>х = -3. х = -7.<br>Отже, X = —3 або х — —7. •<br><br>Усно<br><br>1065. Замініть віднімання додаванням:<br>а) 5-(-2); 6)5-7; в) -3 - 8; г)-6-(-9).<br>1066. Обчисліть:<br>а)-2-5; 6)4-6; в)-3-6; г)-7-(-8).<br><br>Рівень А<br><br>1067. Подайте у вигляді суми різницю:<br>а)-31-(-28); 6) 50-(-32); в)-37-21;<br>г)а-10; д)а-(-9); е)7-(-а).<br> <br>1068. Обчисліть різницю і зробіть перевірку:<br>а) 5-27; б)-5-(-11); в)-7-28;<br>г)-11-15; д) 11 - 39; е)-41-(-5);<br>є)-5-20; ж) 15-(-30); з)-12-7.<br>Виконайте віднімання:<br>1069. а)-19-(-16); б)-18-9; в) 7 -(-40);<br>г) -5 -(-1,5); д) 2,5 -7,5; е)4-(-1,6).<br>[[Image:asd294.jpg]]<br> |
| | + | |
| | + | Замініть віднімання додаванням і обчисліть:<br>1073. а)-1 + 5-(-12); б)-17-8 -(-25); в) 40-(-76)-38.<br> <br>1074.<br> <br>а) 11 - (-7) + (-2); б) 35 - 40 - (-12); в)-5,7 + 15 - 6,6.<br> <br>1075. Обчисліть різниці а - Ь і Ь - а, якщо:<br>а) а = -15; Ь = 35; б) а = 50; Ь = -82; в) а = -120; Ь = 45.<br>Знайдіть модулі різниць і порівняйте ці модулі.<br>Розв 'яжіть рівняння і зробіть перевірку:<br>1076. а)-7+х = -15; б) х + (-35) = -20; в)-11+х = -18.<br> <br>1077.<br> <br>а)х + 9 = 4; б)21+х = -7; в)х + (-15) = -22.<br> <br><br>Знайдіть відстань між двома точками координатної прямої:<br>1078. а)Д-1)і5(4); б) М(-1,5) і N(2,5); в) Д-8,3) і Д-2,1).<br> <br>1079І<br> <br>а) С(-7) і Д-2); б) £(1,3) і ^(7,1); в) М(-3,2) і N(4,8).<br> <br>1080. Увечері температура повітря була -12°С. За ніч вона знизилась на 4°С. Якою стала температура повітря вранці?<br>1081. За день температура повітря знизилась на 5°С і ввечері дорівнювала -1°С. Якою була температура повітря вранці?<br> <br>1082.<br> <br>Температура повітря вранці дорівнювала 3°С, а ввечері стала ^°С. На скільки градусів змінилася температура повітря протягом дня?<br> <br>1083. Температура повітря вранці дорівнювала -5°С, а ввечері стала -9°С Чому дорівнює різниця: а) ранкової та вечірньої температур; б) вечірньої та ранкової температур? Чим відрізняються знайдені різниці?<br><br><br>Рівень Б<br>[[Image:asd295.jpg]]<br> |
| | + | |
| | + | Спростіть вираз:<br> 1086. а)х + 7- 18-х+ 24; б) 4-а-19-11+« + 25.<br> <br> 1087.<br> <br> а)9-с+ ІО + с-71; б) а - 2 + Ь - 18 - Ь - а + 30.<br> <br> Розв 'яжіть рівняння:<br> 1088. а)х+19-25 = -8; б) 10-х-4 = -2; в) 40-х + 35-70 = 8.<br> 1089. а)|х| + 7=11; б) 10,2-|х| = 3,8; в) |х|-5,2 = -2; г)|х-2| = 8; д)|х + 3| = 9; е)|3-х| = 4.<br> <br> 1090.<br> <br> а)8-х + 5 = 15; б) [х|-2,5 = 8,8; в)|х + 5|=1.<br> <br> 1091. Розставте замість зірочок знаки «+» або «-» так, щоб виконувалась<br> рівність:<br> а) 40 * 20 * (-60) * 30 * 50 = 100; б) 80 * 10 * 70 * 50 * (-90) = 100.<br> 1092. На координатній прямій позначені точка А(3) і відрізок АВ завдовжки<br> 5 одиниць. Які координати може мати точка В?<br> <br> <br> Здогадайтеся<br> <br> 1093. Якщо кожному зі своїх дітей мама дасть по 13 слив, то у неї залишиться 8 слив, якщо ж вона дасть кожному по 15 слив, то всі сливи будуть роздані. Скільки слив було в мами?<br> <br> Вправи для повторення<br> 1094. Діаметр круга дорівнює 8 см. Знайдіть площу круга.<br> 1095. У трьох цистернах зберігається бензин. У першій цистерні міститься<br> 5 З<br> — усього бензину, а у другій — Яка частина всього бензину містить-<br> 12 8<br> ся у третій цистерні? Скільки всього бензину у трьох цистернах, якщо у другій цистерні його є 18 т?<br> 1096. Мотоцикліст проїхав 19,5 км, після чого протягом 4 год. рухався зі швидкістю V км/год. Скільки кілометрів проїхав мотоцикліст? Складіть вираз і знайдіть його значення, якщо V = 18.<br> 1097. Щоб проїхати шлях від одного міста до іншого, автомобіль витратив 25 л бензину, а мотоцикл — 8,4 л. На скільки відсотків витрати бензину мотоцикла менші, ніж витрати автомобіля?<br> 1098. Промінь ділить розгорнутий кут на два кути, величина одного з яких становить 125% від величини іншого. Яка величина кожного з утворених кутів?<br> <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту<br> <sub>[[Гіпермаркет Знань - перший в світі!|Календарно-тематичне планування]] математики, [[Математика 6 клас|завдання школяру]] 6 класу, [[Математика|курси учителю]] математики </sub> |
| | | | |
| | '''<u>Зміст уроку</u>''' | | '''<u>Зміст уроку</u>''' |
Версия 22:21, 15 марта 2010
Гіпермаркет Знань>>Математика>>Математика 6 клас>>Віднімання раціональних чисел
Віднімання від'ємних чисел і чисел з різними знаками має такий самий зміст, що й віднімання додатних чисел. Нагадаємо, що за допомогою віднімання знаходять невідомий доданок за відомими сумою й одним з доданків.
Розглянемо приклади.
Оскільки -7 + (-8) = -15, то -15 - (-8) = -7.
Такий же результат одержимо, якщо до числа -15 додамо число, протилежне числу -8, тобто число +8. Тому різницю -15 - (-8) можна замінити сумою -15 + (+8), у якій до зменшуваного додається число, протилежне від'ємнику: -15-(-8) = -15+ (+8) = -7.
Отже, щоб від одного числа відняти інше, досить до зменшуваного додати число, протилежне від'ємнику.
Це правило віднімання можна записати так:
а - Ь = а + (-Ь),
де а і Ь — будь-які раціональні числа. Зокрема, а - а = а + (-а) = 0.
Оскільки віднімання можна замінити додаванням протилежного числа, то будь-який вираз, який містить дії додавання і віднімання, можна записати як суму.
Наприклад, вираз -10 - (+7) є різницею чисел -10 і +7, його можна записати як суму чисел -10 і -7, бо -10 - (+7) = -10 + (-7). Правильно й навпаки: суму чисел -10 і -7 можна записати як різницю чисел -10 і 7, тобто -10 + (-7) -= -10-(+7).
Домовимося надалі додатні числа писати без знака «+», тобто суму -10 + (+7) записуватимемо так: -10 + 7, а різницю 14 - (+18) так: 14 - 18.
Нехай на координатній прямій задано дві точки А(-2) і В(5) (рис. 49) і потрібно знайти довжину відрізка АВ.
Щоб знайти довжину відрізка АВ (або відстань АВ), потрібно дізнатися, скільки одиничних відрізків містить цей відрізок. Як видно з рисунка, довжина відрізка АВ дорівнює 7 одиничним відрізкам. Через координати кінців відрізка АВ його довжина виражається так:
АВ = 5- (-2) = 7.

Отже, щоб знайти довжину відрізка на координатній прямій, потрібно від координати його правого кінця відняти координату лівого кінця.
Для тих, хто хоче знати більше
Якби при відшуканні довжини відрізка АВ (рис. 49) від координати лівого кінця відняли координату правого, то одержали б число -2 - 5 = -7. Довжина відрізка АВ є додатною величиною і в цьому випадку вона дорівнює модулю знайденого числа:
Л£ = |-2-5| = |-7| = 7.
Отже, довжина відрізка АВ дорівнює модулю різниці координат його лівого і правого кінців. Ця довжина також дорівнює модулю різниці координат правого і лівого кінців:
ЛЯ = |5-(-2)| = |5 + 2| = |7| = 7. Довжина відрізка дорівнює модулю різниці координат його кінців.
Довжину відрізка АВ з кінцями А(х) і В(у) можна обчислити за формулою: АВ = \х-у\, або АВ = \у-х\.
Прочитайте
1. Обчислити:-18+15-(-11)-32.
• Запишемо вираз у вигляді суми і згрупуємо числа: -18+ 15-(-11)-32 = -18+ 15 + 11 +(-32) =
= (-18 + (-32)) + (15 + 11) = -50 + 26 = -24. •
2. Спростити вираз: -7 + а+8-а-(-11).
• Запишемо вираз у вигляді суми і згрупуємо доданки: -7 + а + 8-а-(-11) = -7 + <з + 8 + (-а)+11 =
= (-7 + 8 + 11) + (а + (-а))=12 + 0=12. •
3. Розв'язати рівняння: а)х + 10-27 = 13; б)|х + 5| = 2.
• а) Спочатку спростимо вираз у лівій частині рівняння:
х+ 10-27 = х+ 10 + (-27) = х + (-17) = х- 17.
Одержимо рівняння х- 17 = 13, звідки: х = 13 + 17; х = 30.
б) Якщо модуль числа дорівнює 2, то цим числом є 2 або -2, тому
х + 5 = 2 або х + 5 = -2. Розв'яжемо кожне із цих рівнянь.
х + 5 = 2; х + 5 = -2;
х 2 5, х 2 5 у
х = -3. х = -7.
Отже, X = —3 або х — —7. •
Усно
1065. Замініть віднімання додаванням:
а) 5-(-2); 6)5-7; в) -3 - 8; г)-6-(-9).
1066. Обчисліть:
а)-2-5; 6)4-6; в)-3-6; г)-7-(-8).
Рівень А
1067. Подайте у вигляді суми різницю:
а)-31-(-28); 6) 50-(-32); в)-37-21;
г)а-10; д)а-(-9); е)7-(-а).
1068. Обчисліть різницю і зробіть перевірку:
а) 5-27; б)-5-(-11); в)-7-28;
г)-11-15; д) 11 - 39; е)-41-(-5);
є)-5-20; ж) 15-(-30); з)-12-7.
Виконайте віднімання:
1069. а)-19-(-16); б)-18-9; в) 7 -(-40);
г) -5 -(-1,5); д) 2,5 -7,5; е)4-(-1,6).
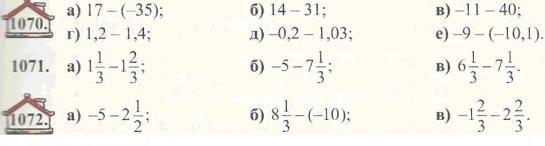
Замініть віднімання додаванням і обчисліть:
1073. а)-1 + 5-(-12); б)-17-8 -(-25); в) 40-(-76)-38.
1074.
а) 11 - (-7) + (-2); б) 35 - 40 - (-12); в)-5,7 + 15 - 6,6.
1075. Обчисліть різниці а - Ь і Ь - а, якщо:
а) а = -15; Ь = 35; б) а = 50; Ь = -82; в) а = -120; Ь = 45.
Знайдіть модулі різниць і порівняйте ці модулі.
Розв 'яжіть рівняння і зробіть перевірку:
1076. а)-7+х = -15; б) х + (-35) = -20; в)-11+х = -18.
1077.
а)х + 9 = 4; б)21+х = -7; в)х + (-15) = -22.
Знайдіть відстань між двома точками координатної прямої:
1078. а)Д-1)і5(4); б) М(-1,5) і N(2,5); в) Д-8,3) і Д-2,1).
1079І
а) С(-7) і Д-2); б) £(1,3) і ^(7,1); в) М(-3,2) і N(4,8).
1080. Увечері температура повітря була -12°С. За ніч вона знизилась на 4°С. Якою стала температура повітря вранці?
1081. За день температура повітря знизилась на 5°С і ввечері дорівнювала -1°С. Якою була температура повітря вранці?
1082.
Температура повітря вранці дорівнювала 3°С, а ввечері стала ^°С. На скільки градусів змінилася температура повітря протягом дня?
1083. Температура повітря вранці дорівнювала -5°С, а ввечері стала -9°С Чому дорівнює різниця: а) ранкової та вечірньої температур; б) вечірньої та ранкової температур? Чим відрізняються знайдені різниці?
Рівень Б
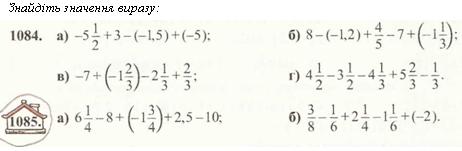
Спростіть вираз:
1086. а)х + 7- 18-х+ 24; б) 4-а-19-11+« + 25.
1087.
а)9-с+ ІО + с-71; б) а - 2 + Ь - 18 - Ь - а + 30.
Розв 'яжіть рівняння:
1088. а)х+19-25 = -8; б) 10-х-4 = -2; в) 40-х + 35-70 = 8.
1089. а)|х| + 7=11; б) 10,2-|х| = 3,8; в) |х|-5,2 = -2; г)|х-2| = 8; д)|х + 3| = 9; е)|3-х| = 4.
1090.
а)8-х + 5 = 15; б) [х|-2,5 = 8,8; в)|х + 5|=1.
1091. Розставте замість зірочок знаки «+» або «-» так, щоб виконувалась
рівність:
а) 40 * 20 * (-60) * 30 * 50 = 100; б) 80 * 10 * 70 * 50 * (-90) = 100.
1092. На координатній прямій позначені точка А(3) і відрізок АВ завдовжки
5 одиниць. Які координати може мати точка В?
Здогадайтеся
1093. Якщо кожному зі своїх дітей мама дасть по 13 слив, то у неї залишиться 8 слив, якщо ж вона дасть кожному по 15 слив, то всі сливи будуть роздані. Скільки слив було в мами?
Вправи для повторення
1094. Діаметр круга дорівнює 8 см. Знайдіть площу круга.
1095. У трьох цистернах зберігається бензин. У першій цистерні міститься
5 З
— усього бензину, а у другій — Яка частина всього бензину містить-
12 8
ся у третій цистерні? Скільки всього бензину у трьох цистернах, якщо у другій цистерні його є 18 т?
1096. Мотоцикліст проїхав 19,5 км, після чого протягом 4 год. рухався зі швидкістю V км/год. Скільки кілометрів проїхав мотоцикліст? Складіть вираз і знайдіть його значення, якщо V = 18.
1097. Щоб проїхати шлях від одного міста до іншого, автомобіль витратив 25 л бензину, а мотоцикл — 8,4 л. На скільки відсотків витрати бензину мотоцикла менші, ніж витрати автомобіля?
1098. Промінь ділить розгорнутий кут на два кути, величина одного з яких становить 125% від величини іншого. Яка величина кожного з утворених кутів?
Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту
Календарно-тематичне планування математики, завдання школяру 6 класу, курси учителю математики
Зміст уроку
 конспект уроку і опорний каркас конспект уроку і опорний каркас
 презентація уроку презентація уроку
 акселеративні методи та інтерактивні технології акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями) закриті вправи (тільки для використання вчителями)
 оцінювання
Практика оцінювання
Практика
 задачі та вправи,самоперевірка задачі та вправи,самоперевірка
 практикуми, лабораторні, кейси практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання
Ілюстрації домашнє завдання
Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати реферати
 фішки для допитливих фішки для допитливих
 шпаргалки шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення
 зовнішнє незалежне тестування (ЗНТ) зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні підручники основні і допоміжні
 тематичні свята, девізи тематичні свята, девізи
 статті статті
 національні особливості національні особливості
 словник термінів словник термінів
 інше
Тільки для вчителів інше
Тільки для вчителів
 ідеальні уроки ідеальні уроки
 календарний план на рік календарний план на рік
 методичні рекомендації методичні рекомендації
 програми програми
 обговорення обговорення
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|