Версия 15:29, 10 февраля 2011Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Окружность. Полные уроки ТЕМА УРОКА: Окружность.
Цели урока
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Помнить каждому нужно, | Файл:06022011 0.gif |
Из истории окружности
Самая простая из всех кривых линий - окружность. Это одна из древнейших геометрических фигур. Философы древности придавали ей большое значение. Согласно Аристотелю, небесная материя, из которой состоят планеты и звезды, как самая совершенная, должна двигаться по самой совершенной линии - окружности. Сотни лет астрономы считали, что планеты двигаются по окружностям. Это ошибочное мнение было опровергнуто лишь в XVII веке учением Коперника, Галилея, Кеплера и Ньютона.
Для первобытных людей важную роль играла форма окружающих их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек деревья и деревья, которые годятся лишь на дрова, вкусные орехи от горьких или ядовитых. Особенно вкусны орехи кокосовой пальмы. Эти орехи очень похожи на шар.А добывая каменную соль или горный кварц, люди наталкивались на кристаллы, потом научились шлифовать их. Отшлифованные орудия позволили быстро срубить дерево, разрезать мясо, помогали лучше охотиться на зверей. Специальных названий для геометрических фигур тогда не было. Говорили: “Такой, как кокосовый орех”, (т. е. круглый), “такой, как соль” (т. е. имеющий форму куба). Некоторые формы фигур казались особо красивыми. И действительно, нельзя без восхищения смотреть на красоту кристаллов, цветов, фигур, имеющих правильную круглую форму.Только в Древней Греции окружность и круг получили свои названия.
Круглые тела в древности заинтересовали человека. Так в Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Позже вместо бревен стали использовать их части – в виде колес, которые катились уже легче.
Окружность и круг
А теперь давайте поближе познакомимся с окружностью и кругом.
Как вы думаете, а чем отличаются эти два понятия?
Окружность и круг - не одно и то же. Окружность - это замкнутая прямая линия, все точки которой расположены на одинаковом расстоянии от одной внутренней точки, которая называется центром. А круг - это часть плоскости, ограниченная окружностью.
Диаметр - это отрезок, который соединяет две точки окружности и проходит через центр этой окружности, это максимальное расстояние между точками одной фигуры. А вот половинка диаметра называется радиусом. Радиус соединяет центр окружности с любой точкой окружности. Есть еще такое необычное слово - хорда. Хорда - это отрезок, который соединяет две точки окружности, но, в отличие от диаметра, хорда не проходит через центр окружности - ей больше нравится находиться около окружности.
Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Для построения окружности необходим новый чертежный инструмент – циркуль.
Геометрические определения
Окружность — геометрическое место точек плоскости, равноудаленных от заданной точки, называемой её центром.
Связанные определения
- Отрезок, соединяющий центр окружности с какой-либо её точкой (а также длина этого отрезка), называется радиусом окружности.
- Часть плоскости, ограниченная окружностью, называется кругом.
- Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.
- Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
- Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
- Прямая, проходящая через две точки окружности, называется секущей.
- Центральным углом в окружности называется плоский угол с вершиной в её центре.
- Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.
- Две окружности, имеющие общий центр, называются концентрическими.
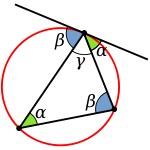 Через вершину треугольника проведена касательная к описанной окружности
Через вершину треугольника проведена касательная к описанной окружности
Основные термины
Касательная.
Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Файл:06022011 4.gif
Свойства касательной
- Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
- Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Хорда.
О'трезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.
Свойства хорд
- Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
- Дуги, заключенные между параллельными хордами, равны.
- Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.
Свойства окружности
- Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
- Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
- Точка касания двух окружностей лежит на линии, соединяющей их центры.
Файл:06022011 11.gif
Файл:T.gif Теорема о касательной и секущей.
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC2 = MA•MB.
Файл:06022011 12.gif Файл:06022011 13.gif
Файл:T.gif Теорема о секущих.
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.
Интересный факт:
А теперь давайте поразмышляем о колесе.
Колесо встречается в самых ранних цивилизациях (Шумер, Египет..), однако его не занли индейцы Америки. Придумали его явно в Старом Свете и скорей всего случайно ))) Навроде, увидили люди катящийся ствол дерева с горы или камни и решили использовать аналогичный механизм )))Кто, когда и зачем впервые придумал колесо, остается одной из самых больших загадок истории.
Самое древнее колесо было найдено на территории Месопотамии, и сделано оно было около 55 веков назад. Различные грузы до этого транспортировались с помощью того, что нынче известно как санки. На шумерской пиктограмме XXXV века до нашей эры впервые было изображено подобие повозки: санки на колесах. Колеса в то время были вырезанными из дерева цельными дисками. Первые колеса со спицами были изобретены на полуострове Малая Азия (самый западный полуостров Азии, ныне принадлежит Турции) в XX веке до н.э. и в том же веке докатились до Европы и до Китая и Индии. Такие колеса использовались только в колесницах для перевозки людей, но в Египте их стали применять и для грузов. Наибольшее распространение колеса и всевозможные повозки получили в Древней Греции, а потом и Риме. В Америке колеса и повозки появились только с приходом туда европейцев.
В Древней Греции круг и окружность считали венцом совершенства. В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности стало толчком к возникновению колеса, так как ось и втулка колеса должны всё время быть в соприкосновении. К сожалению, неизвестен изобретатель колеса. Колесо – это чудо! Что же в нём особенного? – подумаете вы. Но это только на первый взгляд. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезли все колёса!
Круг – колесо – прогресс (движение вперед)
Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы. Не произойдет движения вперед.
Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы. Не произойдет движения вперед.
Самые первые колеса были сделаны в Месопотамии (ныне Ирак) в 3500-3000 гг. до н. э. и представляли собой гончарный круг и тележное колесо.
Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму.
Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность.
Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры. Круглыми были и колонны, подпирающие здания. Самым важным среди круглых тел был шар.
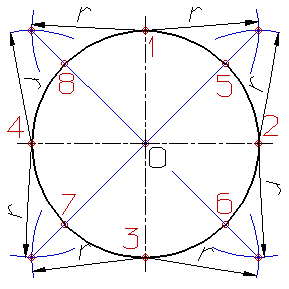
Деление окружности на восемь равных частей.
Деление окружности на восемь равных частей производится в следующей последовательности:
- Проводят две перпендикулярные оси, которые пересекая окружность в точках 1,2,3,4 делят ее на четыре равные части;
- Применяя известный прием деления прямого угла на две равные части при помощи циркуля или угольника строят биссектрисы прямых углов, которые пересекаясь с окружностью в точках 5, 6, 7, и 8 делят каждую четвертую часть окружности пополам.
Так же есть интересный факт про движение по окружности.
Вопросы:
- Сформулируйте определение окружности и круга?
- Что такое хорда?
- Какая разница между диаметром и радиусом?
Список использованных источников:
- Математика • Физика • Справочник.
- Бубенцова Марина Николаевна, учитель математики МОУ СОШ с. Ульяновка, Тамалинского района.
- Элементарная геометрия. В 2 тт.. — М.: МЦНМО, 2004.
Отредактировано и выслано Потурнаком С. А.
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
Предмети > Математика > Математика 7 классАвторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: