Вынужденные колебания. Резонанс

KNOWLEDGE HYPERMARKET

+		Версия 13:21, 8 февраля 2011 (просмотреть исходный код)
User16  (Обсуждение | вклад)
← Предыдущая правка
		Версия 13:22, 8 февраля 2011 (просмотреть исходный код)
User16  (Обсуждение | вклад) 
Следующая правка →
		
Строка 1:
Строка 1:
 <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Физика и астрономия, Физика, 11 класс,  урок, на Тему, Вынужденные колебания, Резонанс</metakeywords>    <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Физика и астрономия, Физика, 11 класс,  урок, на Тему, Вынужденные колебания, Резонанс</metakeywords>  
  
- '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Физика и астрономия|Физика и астрономия]]&gt;&gt;[[Физика 11 класс|Физика 11 класс]]&gt;&gt; Вынужденные колебания. Резонанс'''   + '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Физика и астрономия|Физика и астрономия]]&gt;&gt;[[Физика 11 класс|Физика 11 класс]]&gt;&gt; Вынужденные колебания. Резонанс''' <br> <br>  
- <br> + 
- <br> + 
  
- '''<br>''' + '''<br>'''  
  
- '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; § 25&nbsp;&nbsp;&nbsp;&nbsp; ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС'''<br><br>Как нам известно, свободные колебания затухают за определенное время. + '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; § 25&nbsp;&nbsp;&nbsp;&nbsp; ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС'''<br><br>Как нам известно, свободные колебания затухают за определенное время.  
  
- Но наиболее важное значение имеют незатухающие колебания, — те, которые могут длиться неограниченно долго.<br> + Но наиболее важное значение имеют незатухающие колебания, — те, которые могут длиться неограниченно долго.<br>  
  
- Самый простой способ возбуждения незатухающих колебаний состоит в том, что на систему воздействуют внешней периодической силой. Такие колебания называются вынужденными.<br> + Самый простой способ возбуждения незатухающих колебаний состоит в том, что на систему воздействуют внешней периодической силой. Такие колебания называются вынужденными.<br>  
  
- Работа внешней силы над системой обеспечивает приток энергии к системе извне. Приток энергии не дает колебаниям затухнуть, несмотря на действие сил трения.<br> + Работа внешней силы над системой обеспечивает приток энергии к системе извне. Приток энергии не дает колебаниям затухнуть, несмотря на действие сил трения.<br>  
  
- Особый интерес представляют вынужденные колебания в системе, способной совершать почти свободные колебания. С этим случаем знакомы все, кому приходилось раскачивать ребенка на качелях.<br> + Особый интерес представляют вынужденные колебания в системе, способной совершать почти свободные колебания. С этим случаем знакомы все, кому приходилось раскачивать ребенка на качелях.<br>  
  
- Качели это маятник, т. е. колебательная система с определенной собсшенной частотой. Отклонить качели на больший угол от но;к)лсения равновесия с помощью постоянной во времени небольшой силы невозможно. Не удается раскачать качели и в том случае, если их беспорядочно подталкивать в разные стороны. Однако, если начать в правильном ритме подталкивать каче.пи вперед каждый раз, когда они поравняются с нами, то можно и без большого напряжения раскачать их очень сильно. Правда, для этого потребуется некоторое время. Каждый толчок сам по себе может быть незначительным. После первого толчка качели будут совершать лишь очень малые колебания. Но если темп этих колебаний и внешних толчков один и тот же, то второй толчок будет своевременным и усилит действие первого. Третий усилит ко.тебания еще больше и т. д. Произойдет накопление результатов действия отдельных толчков, и амплитуда колебаний качелей станет большой. Между тем если отдельные толчки следуют друг за другом невпопад, то действие одного будет уничтожаться действием следующего, и заметного эффекта не будет.<br> + Качели это маятник, т. е. колебательная система с определенной собсшенной частотой. Отклонить качели на больший угол от но;к)лсения равновесия с помощью постоянной во времени небольшой силы невозможно. Не удается раскачать качели и в том случае, если их беспорядочно подталкивать в разные стороны. Однако, если начать в правильном ритме подталкивать каче.пи вперед каждый раз, когда они поравняются с нами, то можно и без большого напряжения раскачать их очень сильно. Правда, для этого потребуется некоторое время. Каждый толчок сам по себе может быть незначительным. После первого толчка качели будут совершать лишь очень малые колебания. Но если темп этих колебаний и внешних толчков один и тот же, то второй толчок будет своевременным и усилит действие первого. Третий усилит ко.тебания еще больше и т. д. Произойдет накопление результатов действия отдельных толчков, и амплитуда колебаний качелей станет большой. Между тем если отдельные толчки следуют друг за другом невпопад, то действие одного будет уничтожаться действием следующего, и заметного эффекта не будет.<br>  
  
- Вот эта возможность значительного увеличения амплитуды колебаний системы, способной совершать почти свободные колебания, при совпадении частоты внешней периодической силы с собственной частотой колебательной системы и представляет особый интерес. + Вот эта возможность значительного увеличения амплитуды колебаний системы, способной совершать почти свободные колебания, при совпадении частоты внешней периодической силы с собственной частотой колебательной системы и представляет особый интерес.  
  
- '''Вынужденные колебания шарика, прикрепленного к пружине.''' Рассмотрим вынужденные колебания в системе, обладающей собственной частотой колебаний. Вместо маятника удобнее взять шарик, прикрепленный к пружине. Пусть конец одной из пружин будет прикреплен к нити, перекинутой через блок (рис. 3.12), а нить соединена со стерженьком на диске. Если вращать диск с помощью электродвигателя, то на шарик начнет действовать периодическая внешняя сила.<br><br>[[Image:6.02-76.jpg]]<br><br>Постепенно шарик начнет раскачиваться. При этом амплитуда колебаний будет нарастать. Спустя некоторое время колебания приобретут установившийся характер: их амплитуда перестанет изменяться со временем. Причем можно обнаружить, что частота колебаний шарика<sup>1</sup> равна частоте колебаний конца А пружины, т. е. частоте изменения внешней силы. (Эта частота равна числу оборотов диска в секунду.) + '''Вынужденные колебания шарика, прикрепленного к пружине.''' Рассмотрим вынужденные колебания в системе, обладающей собственной частотой колебаний. Вместо маятника удобнее взять шарик, прикрепленный к пружине. Пусть конец одной из пружин будет прикреплен к нити, перекинутой через блок (рис. 3.12), а нить соединена со стерженьком на диске. Если вращать диск с помощью электродвигателя, то на шарик начнет действовать периодическая внешняя сила.<br><br>[[Image:6.02-76.jpg]]<br><br>Постепенно шарик начнет раскачиваться. При этом амплитуда колебаний будет нарастать. Спустя некоторое время колебания приобретут установившийся характер: их амплитуда перестанет изменяться со временем. Причем можно обнаружить, что частота колебаний шарика<sup>1</sup> равна частоте колебаний конца А пружины, т. е. частоте изменения внешней силы. (Эта частота равна числу оборотов диска в секунду.)  
  
- При установившихся вынужденных колебаниях частота колебаний всегда равна частоте внешней периодически действующей силы. + При установившихся вынужденных колебаниях частота колебаний всегда равна частоте внешней периодически действующей силы.  
  
- Резонанс. Пользуясь установкой, изображенной на рисунке 3.12, выясним, как амплитуда установившихся вынужденных колебаний зависит от частоты внешней силы. Плавно увеличивая частоту внешней силы, мы заметим, что амплитуда колебаний постепенно возрастает. Она достигает максимума, когда внешняя сила действует в такт со свободными колебаниями шарика. + '''Резонанс.''' Пользуясь установкой, изображенной на рисунке 3.12, выясним, как амплитуда установившихся вынужденных колебаний зависит от частоты внешней силы. Плавно увеличивая частоту внешней силы, мы заметим, что амплитуда колебаний постепенно возрастает. Она достигает максимума, когда внешняя сила действует в такт со свободными колебаниями шарика.  
  
- При дальнейшем увеличении частоты амплитуда установившихся колебаний уменьшается. Зависимость амплитуды колебаний от частоты изображена на рисунке 3.13. При очень больших частотах внешней силы амплитуда вынужденных колебаний стремится к нулю с ростом частоты, так как тело, вследствие своей инертности, не успевает заметно смещаться за малые промежутки времени и «дрожит на месте». + При дальнейшем увеличении частоты амплитуда установившихся колебаний уменьшается. Зависимость амплитуды колебаний от частоты изображена на рисунке 3.13. При очень больших частотах внешней силы амплитуда вынужденных колебаний стремится к нулю с ростом частоты, так как тело, вследствие своей инертности, не успевает заметно смещаться за малые промежутки времени и «дрожит на месте».  
  
- Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой ее свободных колебаний называется резонансом (от латинского слова resonans — дающий отзвук).<br>''<br>1 Частоту вынужденных колебаний будем обозначать буквой со в отличие от частоты собственных колебаний системы [[Image:7.02-20.jpg]].''<br>&nbsp;<br>[[Image:6.02-77.jpg]]<br><br>Почему возникает резонанс? Объяснить это явление можно с энергетических позиций. + Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой ее свободных колебаний называется резонансом (от латинского слова resonans — дающий отзвук).<br>''<br>1 Частоту вынужденных колебаний будем обозначать буквой со в отличие от частоты собственных колебаний системы [[Image:7.02-20.jpg]].''<br>&nbsp;<br>[[Image:6.02-77.jpg]]<br><br>Почему возникает резонанс? Объяснить это явление можно с энергетических позиций.  
  
- При резонансе амплитуда вынужденных колебаний максимальна из-за того, что создаются наиболее благоприятные условия для передачи энергии от внешнего источника периодической силы к системе. Внешняя сила при резонансе действует в такт со свободными колебаниями. На протяжении всего периода ее нанравление совпадает с направлением скорости колеблющегося тела. Поэтому на протяжении всего периода эта сила совершает только положительную работу. При установившихся колебаниях положительная работа внешней силы равна по модулю отрицательной работе силы сопротивления. + При резонансе амплитуда вынужденных колебаний максимальна из-за того, что создаются наиболее благоприятные условия для передачи энергии от внешнего источника периодической силы к системе. Внешняя сила при резонансе действует в такт со свободными колебаниями. На протяжении всего периода ее нанравление совпадает с направлением скорости колеблющегося тела. Поэтому на протяжении всего периода эта сила совершает только положительную работу. При установившихся колебаниях положительная работа внешней силы равна по модулю отрицательной работе силы сопротивления.  
  
 Если частота внешней силы не равна собственной частоте [[Image:7.02-20.jpg]] колебаний системы, то внешняя сила лишь в течение части периода совершает положительную работу. В течение же другой части периода направление силы противоположно направлению скорости, и работа внешней силы будет отрицательной. В целом работа внешней силы за период невелика и соответственно невелика и амплитуда установившихся колебаний. Существенное влияние на резонанс оказывает трение в системе. При резонансе положительная работа внешней силы целиком идет на покрытие расхода энергии за счет отрицательной работы силы сопротивления.    Если частота внешней силы не равна собственной частоте [[Image:7.02-20.jpg]] колебаний системы, то внешняя сила лишь в течение части периода совершает положительную работу. В течение же другой части периода направление силы противоположно направлению скорости, и работа внешней силы будет отрицательной. В целом работа внешней силы за период невелика и соответственно невелика и амплитуда установившихся колебаний. Существенное влияние на резонанс оказывает трение в системе. При резонансе положительная работа внешней силы целиком идет на покрытие расхода энергии за счет отрицательной работы силы сопротивления.  
  
- Поэтому чем меньше коэффициент трения, тем больше амплитуда установившихся колебаний. + Поэтому чем меньше коэффициент трения, тем больше амплитуда установившихся колебаний.  
  
- Изменение амплитуды вынужденных колебаний в зависимости от частоты при различных коэффициентах трения и одной и той же амплитуде внешней силы изображено на рисунке 3.14. Кривой 1 соответствует минимальное трение, а кривой 3 — максимальное. На этом рисунке хорошо видно, что возрастание амплитуды вынужденных колебаний при резонансе выражено тем отчетливее, чем меньше трение в системе. + Изменение амплитуды вынужденных колебаний в зависимости от частоты при различных коэффициентах трения и одной и той же амплитуде внешней силы изображено на рисунке 3.14. Кривой 1 соответствует минимальное трение, а кривой 3 — максимальное. На этом рисунке хорошо видно, что возрастание амплитуды вынужденных колебаний при резонансе выражено тем отчетливее, чем меньше трение в системе.  
  
- При малом трении резонанс «острый», а при большом «тупой». Если частота колебаний со далека от резонансной, то амплитуда колебаний мала и почти не зависит от силы сопротивления в системе. + При малом трении резонанс «острый», а при большом «тупой». Если частота колебаний со далека от резонансной, то амплитуда колебаний мала и почти не зависит от силы сопротивления в системе.  
  
- В системе с малым трением амплитуда колебаний при резонансе может быть очень большой даже в том случае, когда внешняя сила мала. Но большая амплитуда устанавливается только спустя продолжительное время после начала действия внешней силы. В соответствии с законом сохранения энергии вызвать в системе колебания с большой амплитудой, а значит, сообидить системе большую энергию небольшой внешней силой можно только за продолжительное время. Если трение велико, то амплитуда колебаний будет небольшой, и для установления колебаний не потребуется много времени. + В системе с малым трением амплитуда колебаний при резонансе может быть очень большой даже в том случае, когда внешняя сила мала. Но большая амплитуда устанавливается только спустя продолжительное время после начала действия внешней силы. В соответствии с законом сохранения энергии вызвать в системе колебания с большой амплитудой, а значит, сообидить системе большую энергию небольшой внешней силой можно только за продолжительное время. Если трение велико, то амплитуда колебаний будет небольшой, и для установления колебаний не потребуется много времени.  
  
- О резонансе имеет смысл говорить, если затухание свободных колебаний в системе достаточно мало. Иначе амплитуда вынужденных колебаний при [[Image:6.02-78.jpg]] будет мало отличаться от амплитуды колебаний при других частотах.<br><br><br><br><br><br> + О резонансе имеет смысл говорить, если затухание свободных колебаний в системе достаточно мало. Иначе амплитуда вынужденных колебаний при [[Image:6.02-78.jpg]] будет мало отличаться от амплитуды колебаний при других частотах.<br><br><br><br><br><br>  
  
 <br> ''Мякишев Г. Я., Физика. 11 класс&nbsp;: учеб. для общеобразоват. учреждений&nbsp;: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М.&nbsp;: Просвещение, 2008. — 399 с&nbsp;: ил.''    <br> ''Мякишев Г. Я., Физика. 11 класс&nbsp;: учеб. для общеобразоват. учреждений&nbsp;: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М.&nbsp;: Просвещение, 2008. — 399 с&nbsp;: ил.''  
Версия 13:22, 8 февраля 2011
 
Гипермаркет знаний>>Физика и астрономия>>Физика 11 класс>> Вынужденные колебания. Резонанс 
 
 

 
                                          § 25     ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС

Как нам известно, свободные колебания затухают за определенное время. 
Но наиболее важное значение имеют незатухающие колебания, — те, которые могут длиться неограниченно долго.
 
Самый простой способ возбуждения незатухающих колебаний состоит в том, что на систему воздействуют внешней периодической силой. Такие колебания называются вынужденными.
 
Работа внешней силы над системой обеспечивает приток энергии к системе извне. Приток энергии не дает колебаниям затухнуть, несмотря на действие сил трения.
 
Особый интерес представляют вынужденные колебания в системе, способной совершать почти свободные колебания. С этим случаем знакомы все, кому приходилось раскачивать ребенка на качелях.
 
Качели это маятник, т. е. колебательная система с определенной собсшенной частотой. Отклонить качели на больший угол от но;к)лсения равновесия с помощью постоянной во времени небольшой силы невозможно. Не удается раскачать качели и в том случае, если их беспорядочно подталкивать в разные стороны. Однако, если начать в правильном ритме подталкивать каче.пи вперед каждый раз, когда они поравняются с нами, то можно и без большого напряжения раскачать их очень сильно. Правда, для этого потребуется некоторое время. Каждый толчок сам по себе может быть незначительным. После первого толчка качели будут совершать лишь очень малые колебания. Но если темп этих колебаний и внешних толчков один и тот же, то второй толчок будет своевременным и усилит действие первого. Третий усилит ко.тебания еще больше и т. д. Произойдет накопление результатов действия отдельных толчков, и амплитуда колебаний качелей станет большой. Между тем если отдельные толчки следуют друг за другом невпопад, то действие одного будет уничтожаться действием следующего, и заметного эффекта не будет.
 
Вот эта возможность значительного увеличения амплитуды колебаний системы, способной совершать почти свободные колебания, при совпадении частоты внешней периодической силы с собственной частотой колебательной системы и представляет особый интерес. 
Вынужденные колебания шарика, прикрепленного к пружине. Рассмотрим вынужденные колебания в системе, обладающей собственной частотой колебаний. Вместо маятника удобнее взять шарик, прикрепленный к пружине. Пусть конец одной из пружин будет прикреплен к нити, перекинутой через блок (рис. 3.12), а нить соединена со стерженьком на диске. Если вращать диск с помощью электродвигателя, то на шарик начнет действовать периодическая внешняя сила.



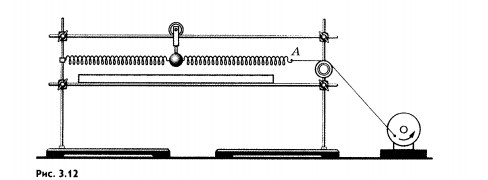
Постепенно шарик начнет раскачиваться. При этом амплитуда колебаний будет нарастать. Спустя некоторое время колебания приобретут установившийся характер: их амплитуда перестанет изменяться со временем. Причем можно обнаружить, что частота колебаний шарика¹ равна частоте колебаний конца А пружины, т. е. частоте изменения внешней силы. (Эта частота равна числу оборотов диска в секунду.) 
При установившихся вынужденных колебаниях частота колебаний всегда равна частоте внешней периодически действующей силы. 
Резонанс. Пользуясь установкой, изображенной на рисунке 3.12, выясним, как амплитуда установившихся вынужденных колебаний зависит от частоты внешней силы. Плавно увеличивая частоту внешней силы, мы заметим, что амплитуда колебаний постепенно возрастает. Она достигает максимума, когда внешняя сила действует в такт со свободными колебаниями шарика. 
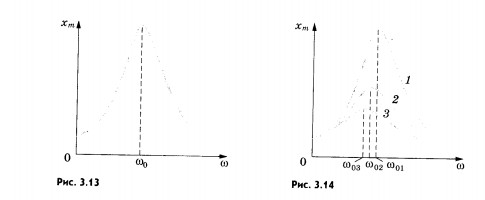
При дальнейшем увеличении частоты амплитуда установившихся колебаний уменьшается. Зависимость амплитуды колебаний от частоты изображена на рисунке 3.13. При очень больших частотах внешней силы амплитуда вынужденных колебаний стремится к нулю с ростом частоты, так как тело, вследствие своей инертности, не успевает заметно смещаться за малые промежутки времени и «дрожит на месте». 
Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой ее свободных колебаний называется резонансом (от латинского слова resonans — дающий отзвук).

1 Частоту вынужденных колебаний будем обозначать буквой со в отличие от частоты собственных колебаний системы .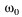
 


Почему возникает резонанс? Объяснить это явление можно с энергетических позиций. 
При резонансе амплитуда вынужденных колебаний максимальна из-за того, что создаются наиболее благоприятные условия для передачи энергии от внешнего источника периодической силы к системе. Внешняя сила при резонансе действует в такт со свободными колебаниями. На протяжении всего периода ее нанравление совпадает с направлением скорости колеблющегося тела. Поэтому на протяжении всего периода эта сила совершает только положительную работу. При установившихся колебаниях положительная работа внешней силы равна по модулю отрицательной работе силы сопротивления. 
Если частота внешней силы не равна собственной частоте 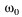 колебаний системы, то внешняя сила лишь в течение части периода совершает положительную работу. В течение же другой части периода направление силы противоположно направлению скорости, и работа внешней силы будет отрицательной. В целом работа внешней силы за период невелика и соответственно невелика и амплитуда установившихся колебаний. Существенное влияние на резонанс оказывает трение в системе. При резонансе положительная работа внешней силы целиком идет на покрытие расхода энергии за счет отрицательной работы силы сопротивления. 
Поэтому чем меньше коэффициент трения, тем больше амплитуда установившихся колебаний. 
Изменение амплитуды вынужденных колебаний в зависимости от частоты при различных коэффициентах трения и одной и той же амплитуде внешней силы изображено на рисунке 3.14. Кривой 1 соответствует минимальное трение, а кривой 3 — максимальное. На этом рисунке хорошо видно, что возрастание амплитуды вынужденных колебаний при резонансе выражено тем отчетливее, чем меньше трение в системе. 
При малом трении резонанс «острый», а при большом «тупой». Если частота колебаний со далека от резонансной, то амплитуда колебаний мала и почти не зависит от силы сопротивления в системе. 
В системе с малым трением амплитуда колебаний при резонансе может быть очень большой даже в том случае, когда внешняя сила мала. Но большая амплитуда устанавливается только спустя продолжительное время после начала действия внешней силы. В соответствии с законом сохранения энергии вызвать в системе колебания с большой амплитудой, а значит, сообидить системе большую энергию небольшой внешней силой можно только за продолжительное время. Если трение велико, то амплитуда колебаний будет небольшой, и для установления колебаний не потребуется много времени. 
О резонансе имеет смысл говорить, если затухание свободных колебаний в системе достаточно мало. Иначе амплитуда вынужденных колебаний при 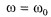 будет мало отличаться от амплитуды колебаний при других частотах.





 

 Мякишев Г. Я., Физика. 11 класс : учеб. для общеобразоват. учреждений : базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с : ил. 

 _{Планирование физике, материалы по физике 11 класса скачать, учебники онлайн} 

 

Содержание урока
 конспект урока
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%92%D1%8B%D0%BD%D1%83%D0%B6%D0%B4%D0%B5%D0%BD%D0%BD%D1%8B%D0%B5_%D0%BA%D0%BE%D0%BB%D0%B5%D0%B1%D0%B0%D0%BD%D0%B8%D1%8F._%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81»
@@ Строка 1: / Строка 1: @@
 <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Физика и астрономия, Физика, 11 класс,  урок, на Тему, Вынужденные колебания, Резонанс</metakeywords>
-'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Физика и астрономия|Физика и астрономия]]&gt;&gt;[[Физика 11 класс|Физика 11 класс]]&gt;&gt; Вынужденные колебания. Резонанс'''
+'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Физика и астрономия|Физика и астрономия]]&gt;&gt;[[Физика 11 класс|Физика 11 класс]]&gt;&gt; Вынужденные колебания. Резонанс''' <br> <br>
-<br>
-<br>
 '''<br>'''
 '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; § 25&nbsp;&nbsp;&nbsp;&nbsp; ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС'''<br><br>Как нам известно, свободные колебания затухают за определенное время.
 Но наиболее важное значение имеют незатухающие колебания, — те, которые могут длиться неограниченно долго.<br>
 Самый простой способ возбуждения незатухающих колебаний состоит в том, что на систему воздействуют внешней периодической силой. Такие колебания называются вынужденными.<br>
 Работа внешней силы над системой обеспечивает приток энергии к системе извне. Приток энергии не дает колебаниям затухнуть, несмотря на действие сил трения.<br>
 Особый интерес представляют вынужденные колебания в системе, способной совершать почти свободные колебания. С этим случаем знакомы все, кому приходилось раскачивать ребенка на качелях.<br>
 Качели это маятник, т. е. колебательная система с определенной собсшенной частотой. Отклонить качели на больший угол от но;к)лсения равновесия с помощью постоянной во времени небольшой силы невозможно. Не удается раскачать качели и в том случае, если их беспорядочно подталкивать в разные стороны. Однако, если начать в правильном ритме подталкивать каче.пи вперед каждый раз, когда они поравняются с нами, то можно и без большого напряжения раскачать их очень сильно. Правда, для этого потребуется некоторое время. Каждый толчок сам по себе может быть незначительным. После первого толчка качели будут совершать лишь очень малые колебания. Но если темп этих колебаний и внешних толчков один и тот же, то второй толчок будет своевременным и усилит действие первого. Третий усилит ко.тебания еще больше и т. д. Произойдет накопление результатов действия отдельных толчков, и амплитуда колебаний качелей станет большой. Между тем если отдельные толчки следуют друг за другом невпопад, то действие одного будет уничтожаться действием следующего, и заметного эффекта не будет.<br>
 Вот эта возможность значительного увеличения амплитуды колебаний системы, способной совершать почти свободные колебания, при совпадении частоты внешней периодической силы с собственной частотой колебательной системы и представляет особый интерес.
 '''Вынужденные колебания шарика, прикрепленного к пружине.''' Рассмотрим вынужденные колебания в системе, обладающей собственной частотой колебаний. Вместо маятника удобнее взять шарик, прикрепленный к пружине. Пусть конец одной из пружин будет прикреплен к нити, перекинутой через блок (рис. 3.12), а нить соединена со стерженьком на диске. Если вращать диск с помощью электродвигателя, то на шарик начнет действовать периодическая внешняя сила.<br><br>[[Image:6.02-76.jpg]]<br><br>Постепенно шарик начнет раскачиваться. При этом амплитуда колебаний будет нарастать. Спустя некоторое время колебания приобретут установившийся характер: их амплитуда перестанет изменяться со временем. Причем можно обнаружить, что частота колебаний шарика<sup>1</sup> равна частоте колебаний конца А пружины, т. е. частоте изменения внешней силы. (Эта частота равна числу оборотов диска в секунду.)
 При установившихся вынужденных колебаниях частота колебаний всегда равна частоте внешней периодически действующей силы.
-Резонанс. Пользуясь установкой, изображенной на рисунке 3.12, выясним, как амплитуда установившихся вынужденных колебаний зависит от частоты внешней силы. Плавно увеличивая частоту внешней силы, мы заметим, что амплитуда колебаний постепенно возрастает. Она достигает максимума, когда внешняя сила действует в такт со свободными колебаниями шарика.
+'''Резонанс.''' Пользуясь установкой, изображенной на рисунке 3.12, выясним, как амплитуда установившихся вынужденных колебаний зависит от частоты внешней силы. Плавно увеличивая частоту внешней силы, мы заметим, что амплитуда колебаний постепенно возрастает. Она достигает максимума, когда внешняя сила действует в такт со свободными колебаниями шарика.
 При дальнейшем увеличении частоты амплитуда установившихся колебаний уменьшается. Зависимость амплитуды колебаний от частоты изображена на рисунке 3.13. При очень больших частотах внешней силы амплитуда вынужденных колебаний стремится к нулю с ростом частоты, так как тело, вследствие своей инертности, не успевает заметно смещаться за малые промежутки времени и «дрожит на месте».
 Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой ее свободных колебаний называется резонансом (от латинского слова resonans — дающий отзвук).<br>''<br>1 Частоту вынужденных колебаний будем обозначать буквой со в отличие от частоты собственных колебаний системы [[Image:7.02-20.jpg]].''<br>&nbsp;<br>[[Image:6.02-77.jpg]]<br><br>Почему возникает резонанс? Объяснить это явление можно с энергетических позиций.
 При резонансе амплитуда вынужденных колебаний максимальна из-за того, что создаются наиболее благоприятные условия для передачи энергии от внешнего источника периодической силы к системе. Внешняя сила при резонансе действует в такт со свободными колебаниями. На протяжении всего периода ее нанравление совпадает с направлением скорости колеблющегося тела. Поэтому на протяжении всего периода эта сила совершает только положительную работу. При установившихся колебаниях положительная работа внешней силы равна по модулю отрицательной работе силы сопротивления.
 Если частота внешней силы не равна собственной частоте [[Image:7.02-20.jpg]] колебаний системы, то внешняя сила лишь в течение части периода совершает положительную работу. В течение же другой части периода направление силы противоположно направлению скорости, и работа внешней силы будет отрицательной. В целом работа внешней силы за период невелика и соответственно невелика и амплитуда установившихся колебаний. Существенное влияние на резонанс оказывает трение в системе. При резонансе положительная работа внешней силы целиком идет на покрытие расхода энергии за счет отрицательной работы силы сопротивления.
 Поэтому чем меньше коэффициент трения, тем больше амплитуда установившихся колебаний.
 Изменение амплитуды вынужденных колебаний в зависимости от частоты при различных коэффициентах трения и одной и той же амплитуде внешней силы изображено на рисунке 3.14. Кривой 1 соответствует минимальное трение, а кривой 3 — максимальное. На этом рисунке хорошо видно, что возрастание амплитуды вынужденных колебаний при резонансе выражено тем отчетливее, чем меньше трение в системе.
 При малом трении резонанс «острый», а при большом «тупой». Если частота колебаний со далека от резонансной, то амплитуда колебаний мала и почти не зависит от силы сопротивления в системе.
 В системе с малым трением амплитуда колебаний при резонансе может быть очень большой даже в том случае, когда внешняя сила мала. Но большая амплитуда устанавливается только спустя продолжительное время после начала действия внешней силы. В соответствии с законом сохранения энергии вызвать в системе колебания с большой амплитудой, а значит, сообидить системе большую энергию небольшой внешней силой можно только за продолжительное время. Если трение велико, то амплитуда колебаний будет небольшой, и для установления колебаний не потребуется много времени.
 О резонансе имеет смысл говорить, если затухание свободных колебаний в системе достаточно мало. Иначе амплитуда вынужденных колебаний при [[Image:6.02-78.jpg]] будет мало отличаться от амплитуды колебаний при других частотах.<br><br><br><br><br><br>
 <br> ''Мякишев Г. Я., Физика. 11 класс&nbsp;: учеб. для общеобразоват. учреждений&nbsp;: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М.&nbsp;: Просвещение, 2008. — 399 с&nbsp;: ил.''

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: