Динамический хаос в изолированной популяции

KNOWLEDGE HYPERMARKET

 		Версия 08:55, 28 марта 2012 (просмотреть исходный код)
User16  (Обсуждение | вклад)
 (Новая страница: «<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Естествознание, 11 класс, Ди...»)
← Предыдущая правка
		Версия 09:05, 28 марта 2012 (просмотреть исходный код)
User16  (Обсуждение | вклад) 
Следующая правка →
		
Строка 5:
Строка 5:
 <br>    <br>  
  
- <br>6.5. Динамический хаос в изолированной популяции <br><br>Будем&nbsp; рассматривать&nbsp; какую-нибудь&nbsp; изолированную&nbsp; популяцию,&nbsp; например популяцию насекомых на удаленном острове в открытом океане. Как известно, многие насекомые выводятся весной, лето живут, а осенью откладывают оплодотворенные яйца. При таком цикле воспроизводства поколения не перекрываются, все особи одного возраста. Говорят, что состояние популяции меняется дискретно во времени, поэтапно, одно за другим. Обозначим начальное&nbsp; состояние популяции через Хо,&nbsp; а Хn -&nbsp; её численность через n лет. Коэффициентом прироста R будем называть относительную величину изме-<br>нения численности популяции за год: &nbsp;<br><br>R =&nbsp; (Хn+1 - Хn)/Хn. Если считать R = const,&nbsp; то рост популяции будет определяться зависимостью (6.2) <br><br>X n+1 = (1 + R) Xn .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.2) <br><br>Через n лет численность популяции будет равна <br><br>Xn = (1 + R)n X0 .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.3) <br><br>Формула (6.3) предсказывает неограниченный рост популяции, что нереально.&nbsp; Чтобы&nbsp; быть&nbsp; ближе&nbsp; к&nbsp; действительной&nbsp; ситуации&nbsp; в&nbsp; биоценозах,&nbsp; П.Ф. Ферхюльст&nbsp; ещё&nbsp; в 1845&nbsp; г.&nbsp; постулировал,&nbsp; что&nbsp; коэффициент&nbsp; прироста R меняется в зависимости от достигнутой численности. Считая, что для данной экологической&nbsp; ниши&nbsp; имеется&nbsp; конкретный&nbsp; предел&nbsp; численности&nbsp; популяции, равный Хмах, Ферхюльст положил R = r( Хmax - Хn). С математической точки зрения удобнее выражать численность популяции в относительных единицах и положить R = r (1 - Хn). Коэффициент пропорциональности r мы будем называть&nbsp; управляющим параметром, или параметром&nbsp; роста. Когда&nbsp; r &lt;&nbsp; 1,&nbsp; численность&nbsp; популяции&nbsp; растет,&nbsp; пока&nbsp; не&nbsp; достигнет&nbsp; Хmax =&nbsp; 1,&nbsp; при&nbsp; котором&nbsp; рост <br>прекращается. &nbsp;<br><br>Формула, описывающая изменения численности популяции, теперь будет следующий вид: <br><br>X n+1 = (1 + R) Xn - r Хn2 .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.4) <br><br>Будем следить за эволюцией популяции на последующих шагах, то есть при увеличении n. На первый взгляд уравнение (6.4) достаточно простое и не предвещает&nbsp; резких&nbsp; перемен. Но&nbsp; все&nbsp; дело&nbsp; в&nbsp; нелинейности,&nbsp; она&nbsp; приводит&nbsp; к сложным циклическим зависимостям, представленным на рис. 6.10. <br><br>rfhn<br>&nbsp;<br>Рис. 6.10. Варианты изменений численности популяции &nbsp;<br><br>Для&nbsp; области&nbsp; значений&nbsp; параметра&nbsp; воспроизводства&nbsp; от 0&nbsp; до 1&nbsp; численность популяции при любых начальных значениях все равно стремится к нулевому конечному уровню, физически это означает вымирание популяции. <br><br>Когда параметр воспроизводства 1 &lt; r &lt; 2 , кривые роста плавно достигают&nbsp; стационарного уровня, после чего каждый&nbsp; год появляется новая популяция, точно замещающая предыдущую. <br><br>При условии r = 2 происходит первая бифуркация, становятся возможными два варианта: численность популяции попеременно осциллирует между двумя уровнями. Прогноз развития достаточно определенный: после многих лет размножения мы встретим на острове либо высокий уровень численности насекомых, либо низкий. Объяснение можно дать простое: когда насекомых очень много, они истощают имеющиеся пищевые ресурсы и потомство оказывается в кризисных условиях перенаселения (по сравнению с малыми ресурсами). Наоборот, для малой численности при неистощенных ресурсах создаются благоприятные условия жизни и откладывается большое количество яиц, на будущий год потомство будет многочисленным. <br><br>Когда&nbsp; значения&nbsp; параметра&nbsp; воспроизводства&nbsp; задаются (исследователем) большими&nbsp; чем 2,449,&nbsp; появляется&nbsp; вторая бифуркация&nbsp; и&nbsp; теперь&nbsp; численность&nbsp; популяции&nbsp; колеблется между&nbsp; четырьмя&nbsp; уровнями&nbsp; значений.&nbsp; Критические&nbsp; значения параметра воспроизводства на&nbsp; числовой оси лежат все ближе друг к другу, и при каждом из них происходит&nbsp; разбиение на два уровня. В итоге прогноз развития популяции становится неопределенным, так как&nbsp; становятся&nbsp; возможными&nbsp; самые&nbsp; разные&nbsp; значения для любого&nbsp; года: от минимального&nbsp; до&nbsp; максимального.&nbsp; В&nbsp; таких случаях&nbsp; говорят,&nbsp; что&nbsp; в&nbsp; системе,&nbsp; описываемой&nbsp; уравнениями&nbsp; типа (6.4),&nbsp; устанавливается&nbsp; динамический&nbsp; хаос. Более подробно этот вопрос будет разбираться при выполнении компьютерных работ,&nbsp; поэтому&nbsp; здесь&nbsp; отметим&nbsp; лишь,&nbsp; что&nbsp; общее&nbsp; представление&nbsp; о&nbsp; поведении многих&nbsp; физических,&nbsp; химических&nbsp; и&nbsp; биологических&nbsp; нелинейных&nbsp; систем,&nbsp; подобных рассмотренной нами, может дать диаграмма Фейгенбаума. Конечно, для многих животных&nbsp; коэффициент&nbsp; прироста&nbsp; популяции&nbsp; равный 230%&nbsp; или 250% не реален, однако для насекомых это не предел. <br><br>rfhn<br><br>Рис. 6.11. Диаграмма&nbsp; Фейгенбаума для&nbsp; бифуркационного процесса <br><br>В 1963&nbsp; г.&nbsp; Э.Н.&nbsp; Лоренц&nbsp; обнаружил,&nbsp; что&nbsp; бифуркационное&nbsp; поведение свойственно&nbsp; турбулентному потоку.&nbsp; Затем&nbsp; оно&nbsp; было&nbsp; выявлено&nbsp; в исследованиях&nbsp; по&nbsp; лазерной&nbsp; физике&nbsp; и&nbsp; в&nbsp; кинетике&nbsp; химических&nbsp; реакций.&nbsp; В&nbsp; настоящее время признано, что сценарий удвоения численности элементов нелинейных систем, их энергетических и структурных состояний является универсальным законом природы. Достаточно&nbsp; сказать,&nbsp; что&nbsp; данная&nbsp; закономерность проявляется&nbsp; и&nbsp; в&nbsp; нелинейных&nbsp; колебаниях&nbsp; в&nbsp; электрических&nbsp; сетях (в&nbsp; них могут&nbsp; появляться&nbsp; черты&nbsp; детерминированного&nbsp; хаоса),&nbsp; и в&nbsp; переходе&nbsp; нормального&nbsp; ритма сердца в угрожающую жизни человека фибрилляцию.<br>&nbsp; <br>Существуют&nbsp; и&nbsp; другие&nbsp; пути,&nbsp; приводящие&nbsp; к&nbsp; появлению&nbsp; динамического хаоса. В 1980&nbsp; г. Б.Б. Мандельброт обнаружил, что существует более общий&nbsp;&nbsp; 153принцип перехода от порядка к хаосу, если от действительных значений некоторых управляющих параметров перейти в плоскость комплексных чисел. Процесс Мандельброта для дискретных изменений в принципе эквивалентен процессу Ферхюльста [13] : <br><br>&nbsp;Xn+1 = X 2n + C,<br>&nbsp; <br>где С - некоторая константа, могущая быть комплексным числом. <br><br>Выберем&nbsp; произвольное&nbsp; число&nbsp; Х0,&nbsp; возведем&nbsp; его&nbsp; в&nbsp; квадрат&nbsp; и&nbsp; прибавим константу С; полученное значение нанесем на комплексную плоскость. Затем повторим процесс - сделаем итерацию и отметим новое положение. &nbsp;<br><br>При С = 0 имеются&nbsp; три&nbsp; типа&nbsp; траекторий точки в зависимости от начального значения Х0. Если&nbsp; оно&nbsp; не&nbsp; превосходит&nbsp; единицу,&nbsp; то&nbsp; последующие квадраты будут&nbsp; все меньше и меньше и&nbsp; точка&nbsp; стремится&nbsp; к&nbsp; нулю.&nbsp; Говорят,&nbsp; что&nbsp; ноль является&nbsp; аттрактором&nbsp; для&nbsp; итерационного&nbsp; процесса.&nbsp; Все&nbsp; точки,&nbsp; находящиеся&nbsp; на&nbsp; расстоянии меньше 1 от этого аттрактора движутся к нему. Наоборот,&nbsp; все&nbsp; точки&nbsp; находящиеся&nbsp; на&nbsp; расстоянии больше 1 от ноля будут уходить на бесконечность,&nbsp; так&nbsp; как&nbsp; значения&nbsp; квадратов&nbsp; будут только&nbsp; возрастать. Наконец&nbsp; точки, находящиеся&nbsp; на&nbsp; расстоянии 1&nbsp; от&nbsp; нуля&nbsp; будут&nbsp; оставаться неподвижными.&nbsp; Окружность&nbsp; единичного&nbsp; радиуса является&nbsp; границей между сферами влияния двух аттракторов - нуля и бесконечности. &nbsp;<br><br>rfhn<br>Рис. 6.12. Форма бассейна для аттрактора в точке 0 <br>Рис. 6.14. Форма множества Мандельброта<br>Рис. 6.13. Форма части&nbsp; множества Жюлиа <br><br>Когда&nbsp; константой&nbsp; C&nbsp; является&nbsp; комплексное число, то границы между несколькими (или <br>очень&nbsp; многими)&nbsp; аттракторами&nbsp; перестают&nbsp; быть гладкими. Линия&nbsp; границы выглядит непрерывно&nbsp; изломанной,&nbsp; причем&nbsp; при&nbsp; увеличении&nbsp; масштаба графика во сколько угодно раз ее форма остается подобной себе. Такое свойство границ Мандельброт&nbsp; назвал&nbsp; фрактальной&nbsp;&nbsp; структурой. Здесь&nbsp; физические&nbsp; процессы&nbsp; хаотичны&nbsp; до&nbsp; предела,&nbsp; так&nbsp; как&nbsp; совершается&nbsp; переход&nbsp; из&nbsp; сферы влияния&nbsp; одних&nbsp; закономерностей&nbsp; к&nbsp; сфере&nbsp; влияния другой. Отражая хаос, сама линия (множество&nbsp; точек&nbsp; которой&nbsp; носит&nbsp; название&nbsp; множеств Жюлиа)&nbsp; ок зывается эстетически&nbsp; чень&nbsp; красивой. &nbsp;<br><br>Существует правило, указывающее, какой вид имеет множество Жюлиа для всех возможных&nbsp; значений&nbsp; параметра&nbsp; С.&nbsp; Графически&nbsp; оно&nbsp; выражается&nbsp; множеством Мандельброта [13]. <br>&nbsp;<br>Компьютерное&nbsp; моделирование&nbsp; множеств&nbsp; Жюлиа&nbsp; позволило&nbsp; сравнить их форму с формой многих естественных образований - морского берега, морозного узора на стекле, фигур электрических разрядов, формы ракушек, атмосферных&nbsp; вихрей&nbsp; и&nbsp; других&nbsp; форм&nbsp; движения&nbsp; или&nbsp; результатов&nbsp; физикохимических процессов. &nbsp;<br><br>Как&nbsp; оказалось,&nbsp; наблюдается&nbsp; поразительное&nbsp; сходство&nbsp; типов фигур,&nbsp; несмотря&nbsp; на&nbsp; различие&nbsp; конкретных&nbsp; процессов&nbsp; и&nbsp; их&nbsp; масштабов. Очевидно,&nbsp; что единственная общая черта столь широкого круга процессов - их нелинейная динамика. Нелинейные процессы имеют фрактальные свойства. <br><br><br><br> + <br>'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; 6.5. Динамический хаос в изолированной популяции '''<br><br>Будем&nbsp; рассматривать&nbsp; какую-нибудь&nbsp; изолированную&nbsp; популяцию,&nbsp; например популяцию насекомых на удаленном острове в открытом океане. Как известно, многие насекомые выводятся весной, лето живут, а осенью откладывают оплодотворенные яйца. При таком цикле воспроизводства поколения не перекрываются, все особи одного возраста. Говорят, что состояние популяции меняется дискретно во времени, поэтапно, одно за другим. Обозначим начальное&nbsp; состояние популяции через Х<sub>о</sub>,&nbsp; а Х<sub>n</sub> -&nbsp; её численность через n лет. Коэффициентом прироста R будем называть относительную величину изменения численности популяции за год: &nbsp;<br><br>R =&nbsp; (Х<sub>n+1</sub> - Х<sub>n</sub>)/Х<sub>n</sub>. Если считать R =''const'',&nbsp; то рост популяции будет определяться зависимостью (6.2) <br><br>'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; X <sub>n+1</sub> = (1 + R) X<sub>n</sub> .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.2) '''<br><br>Через n лет численность популяции будет равна <br>'''<br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; X<sub>n</sub> = (1 + R)<sub>n</sub> X<sub>0</sub> .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.3) '''<br><br>Формула (6.3) предсказывает неограниченный рост популяции, что нереально.&nbsp; Чтобы&nbsp; быть&nbsp; ближе&nbsp; к&nbsp; действительной&nbsp; ситуации&nbsp; в&nbsp; биоценозах,&nbsp; П.Ф. Ферхюльст&nbsp; ещё&nbsp; в 1845&nbsp; г.&nbsp; постулировал,&nbsp; что&nbsp; коэффициент&nbsp; прироста R меняется в зависимости от достигнутой численности. Считая, что для данной экологической&nbsp; ниши&nbsp; имеется&nbsp; конкретный&nbsp; предел&nbsp; численности&nbsp; популяции, равный Х<sub>мах</sub>, Ферхюльст положил R = r( Х<sub>max</sub> - Х<sub>n</sub>). С математической точки зрения удобнее выражать численность популяции в относительных единицах и положить R = r (1 - Х<sub>n</sub>). Коэффициент пропорциональности r мы будем называть&nbsp; управляющим параметром, или параметром&nbsp; роста. Когда&nbsp; r &lt;&nbsp; 1,&nbsp; численность&nbsp; популяции&nbsp; растет,&nbsp; пока&nbsp; не&nbsp; достигнет&nbsp; Х<sub>max</sub> =&nbsp; 1,&nbsp; при&nbsp; котором&nbsp; рост прекращается. &nbsp;<br><br>Формула, описывающая изменения численности популяции, теперь будет следующий вид: <br><br>'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; X <sub>n+1</sub> = (1 + R) X<sub>n</sub> - r Х<sub>n</sub><sup>2</sup> .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.4) '''<br><br>Будем следить за эволюцией популяции на последующих шагах, то есть при увеличении n. На первый взгляд уравнение (6.4) достаточно простое и не предвещает&nbsp; резких&nbsp; перемен. Но&nbsp; все&nbsp; дело&nbsp; в&nbsp; нелинейности,&nbsp; она&nbsp; приводит&nbsp; к сложным циклическим зависимостям, представленным на рис. 6.10. 
  +  
  + <br>[[Image:1-03-01.jpg]]<br><br>Для&nbsp; области&nbsp; значений&nbsp; параметра&nbsp; воспроизводства&nbsp; от 0&nbsp; до 1&nbsp; численность популяции при любых начальных значениях все равно стремится к нулевому конечному уровню, физически это означает вымирание популяции. <br><br>Когда параметр воспроизводства 1 &lt; r &lt; 2 , кривые роста плавно достигают&nbsp; стационарного уровня, после чего каждый&nbsp; год появляется новая популяция, точно замещающая предыдущую. <br><br>При условии r = 2 происходит первая бифуркация, становятся возможными два варианта: численность популяции попеременно осциллирует между двумя уровнями. Прогноз развития достаточно определенный: после многих лет размножения мы встретим на острове либо высокий уровень численности насекомых, либо низкий. Объяснение можно дать простое: когда насекомых очень много, они истощают имеющиеся пищевые ресурсы и потомство оказывается в кризисных условиях перенаселения (по сравнению с малыми ресурсами). Наоборот, для малой численности при неистощенных ресурсах создаются благоприятные условия жизни и откладывается большое количество яиц, на будущий год потомство будет многочисленным. <br><br>Когда&nbsp; значения&nbsp; параметра&nbsp; воспроизводства&nbsp; задаются (исследователем) большими&nbsp; чем 2,449,&nbsp; появляется&nbsp; вторая бифуркация&nbsp; и&nbsp; теперь&nbsp; численность&nbsp; популяции&nbsp; колеблется между&nbsp; четырьмя&nbsp; уровнями&nbsp; значений.&nbsp; Критические&nbsp; значения параметра воспроизводства на&nbsp; числовой оси лежат все ближе друг к другу, и при каждом из них происходит&nbsp; разбиение на два уровня. В итоге прогноз развития популяции становится неопределенным, так как&nbsp; становятся&nbsp; возможными&nbsp; самые&nbsp; разные&nbsp; значения для любого&nbsp; года: от минимального&nbsp; до&nbsp; максимального.&nbsp; В&nbsp; таких случаях&nbsp; говорят,&nbsp; что&nbsp; в&nbsp; системе,&nbsp; описываемой&nbsp; уравнениями&nbsp; типа (6.4),&nbsp; устанавливается&nbsp; динамический&nbsp; хаос. Более подробно этот вопрос будет разбираться при выполнении компьютерных работ,&nbsp; поэтому&nbsp; здесь&nbsp; отметим&nbsp; лишь,&nbsp; что&nbsp; общее&nbsp; представление&nbsp; о&nbsp; поведении многих&nbsp; физических,&nbsp; химических&nbsp; и&nbsp; биологических&nbsp; нелинейных&nbsp; систем,&nbsp; подобных рассмотренной нами, может дать диаграмма Фейгенбаума. Конечно, для многих животных&nbsp; коэффициент&nbsp; прироста&nbsp; популяции&nbsp; равный 230%&nbsp; или 250% не реален, однако для насекомых это не предел. 
  +  
  + <br>[[Image:1-03-02.jpg]]<br><br>В 1963&nbsp; г.&nbsp; Э.Н.&nbsp; Лоренц&nbsp; обнаружил,&nbsp; что&nbsp; бифуркационное&nbsp; поведение свойственно&nbsp; турбулентному потоку.&nbsp; Затем&nbsp; оно&nbsp; было&nbsp; выявлено&nbsp; в исследованиях&nbsp; по&nbsp; лазерной&nbsp; физике&nbsp; и&nbsp; в&nbsp; кинетике&nbsp; химических&nbsp; реакций.&nbsp; В&nbsp; настоящее время признано, что сценарий удвоения численности элементов нелинейных систем, их энергетических и структурных состояний является универсальным законом природы. Достаточно&nbsp; сказать,&nbsp; что&nbsp; данная&nbsp; закономерность проявляется&nbsp; и&nbsp; в&nbsp; нелинейных&nbsp; колебаниях&nbsp; в&nbsp; электрических&nbsp; сетях (в&nbsp; них могут&nbsp; появляться&nbsp; черты&nbsp; детерминированного&nbsp; хаоса),&nbsp; и в&nbsp; переходе&nbsp; нормального&nbsp; ритма сердца в угрожающую жизни человека фибрилляцию.<br>&nbsp; <br>Существуют&nbsp; и&nbsp; другие&nbsp; пути,&nbsp; приводящие&nbsp; к&nbsp; появлению&nbsp; динамического хаоса. В 1980&nbsp; г. Б.Б. Мандельброт обнаружил, что существует более общий&nbsp;&nbsp; 153принцип перехода от порядка к хаосу, если от действительных значений некоторых управляющих параметров перейти в плоскость комплексных чисел. Процесс Мандельброта для дискретных изменений в принципе эквивалентен процессу Ферхюльста [13]&nbsp;: <br>'''<br>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; X<sub>n+1</sub> = X <sup>2</sup><sub>n</sub> + C,'''<br>&nbsp; <br>где С - некоторая константа, могущая быть комплексным числом. <br><br>Выберем&nbsp; произвольное&nbsp; число&nbsp; Х0,&nbsp; возведем&nbsp; его&nbsp; в&nbsp; квадрат&nbsp; и&nbsp; прибавим константу С; полученное значение нанесем на комплексную плоскость. Затем повторим процесс - сделаем итерацию и отметим новое положение. &nbsp;<br><br>При С = 0 имеются&nbsp; три&nbsp; типа&nbsp; траекторий точки в зависимости от начального значения Х0. Если&nbsp; оно&nbsp; не&nbsp; превосходит&nbsp; единицу,&nbsp; то&nbsp; последующие квадраты будут&nbsp; все меньше и меньше и&nbsp; точка&nbsp; стремится&nbsp; к&nbsp; нулю.&nbsp; Говорят,&nbsp; что&nbsp; ноль является&nbsp; аттрактором&nbsp; для&nbsp; итерационного&nbsp; процесса.&nbsp; Все&nbsp; точки,&nbsp; находящиеся&nbsp; на&nbsp; расстоянии меньше 1 от этого аттрактора движутся к нему. Наоборот,&nbsp; все&nbsp; точки&nbsp; находящиеся&nbsp; на&nbsp; расстоянии больше 1 от ноля будут уходить на бесконечность,&nbsp; так&nbsp; как&nbsp; значения&nbsp; квадратов&nbsp; будут только&nbsp; возрастать. Наконец&nbsp; точки, находящиеся&nbsp; на&nbsp; расстоянии 1&nbsp; от&nbsp; нуля&nbsp; будут&nbsp; оставаться неподвижными.&nbsp; Окружность&nbsp; единичного&nbsp; радиуса является&nbsp; границей между сферами влияния двух аттракторов - нуля и бесконечности. &nbsp;<br><br>[[Image:1-03-03.jpg]]<br><br>Когда&nbsp; константой&nbsp; C&nbsp; является&nbsp; комплексное число, то границы между несколькими (или очень&nbsp; многими)&nbsp; аттракторами&nbsp; перестают&nbsp; быть гладкими. Линия&nbsp; границы выглядит непрерывно&nbsp; изломанной,&nbsp; причем&nbsp; при&nbsp; увеличении&nbsp; масштаба графика во сколько угодно раз ее форма остается подобной себе. Такое свойство границ Мандельброт&nbsp; назвал&nbsp; фрактальной&nbsp;&nbsp; структурой. Здесь&nbsp; физические&nbsp; процессы&nbsp; хаотичны&nbsp; до&nbsp; предела,&nbsp; так&nbsp; как&nbsp; совершается&nbsp; переход&nbsp; из&nbsp; сферы влияния&nbsp; одних&nbsp; закономерностей&nbsp; к&nbsp; сфере&nbsp; влияния другой. Отражая хаос, сама линия (множество&nbsp; точек&nbsp; которой&nbsp; носит&nbsp; название&nbsp; множеств Жюлиа)&nbsp; ок зывается эстетически&nbsp; чень&nbsp; красивой. &nbsp;<br><br>Существует правило, указывающее, какой вид имеет множество Жюлиа для всех возможных&nbsp; значений&nbsp; параметра&nbsp; С.&nbsp; Графически&nbsp; оно&nbsp; выражается&nbsp; множеством Мандельброта [13]. <br>&nbsp;<br>Компьютерное&nbsp; моделирование&nbsp; множеств&nbsp; Жюлиа&nbsp; позволило&nbsp; сравнить их форму с формой многих естественных образований - морского берега, морозного узора на стекле, фигур электрических разрядов, формы ракушек, атмосферных&nbsp; вихрей&nbsp; и&nbsp; других&nbsp; форм&nbsp; движения&nbsp; или&nbsp; результатов&nbsp; физикохимических процессов. &nbsp;<br><br>Как&nbsp; оказалось,&nbsp; наблюдается&nbsp; поразительное&nbsp; сходство&nbsp; типов фигур,&nbsp; несмотря&nbsp; на&nbsp; различие&nbsp; конкретных&nbsp; процессов&nbsp; и&nbsp; их&nbsp; масштабов. Очевидно,&nbsp; что единственная общая черта столь широкого круга процессов - их нелинейная динамика. Нелинейные процессы имеют фрактальные свойства. <br><br><br><br> 
  
 <br>    <br>  
Версия 09:05, 28 марта 2012
 
Гипермаркет знаний>>Естествознание>>Естествознание 11 класс>> Динамический хаос в изолированной популяции 

 

                                                           6.5. Динамический хаос в изолированной популяции 

Будем  рассматривать  какую-нибудь  изолированную  популяцию,  например популяцию насекомых на удаленном острове в открытом океане. Как известно, многие насекомые выводятся весной, лето живут, а осенью откладывают оплодотворенные яйца. При таком цикле воспроизводства поколения не перекрываются, все особи одного возраста. Говорят, что состояние популяции меняется дискретно во времени, поэтапно, одно за другим. Обозначим начальное  состояние популяции через Х_о,  а Х_n -  её численность через n лет. Коэффициентом прироста R будем называть относительную величину изменения численности популяции за год:  

R =  (Х_n+1 - Х_n)/Х_n. Если считать R =const,  то рост популяции будет определяться зависимостью (6.2) 

                                                              X _n+1 = (1 + R) X_n .                                              (6.2) 

Через n лет численность популяции будет равна 

                                                              X_n = (1 + R)_n X₀ .                                               (6.3) 

Формула (6.3) предсказывает неограниченный рост популяции, что нереально.  Чтобы  быть  ближе  к  действительной  ситуации  в  биоценозах,  П.Ф. Ферхюльст  ещё  в 1845  г.  постулировал,  что  коэффициент  прироста R меняется в зависимости от достигнутой численности. Считая, что для данной экологической  ниши  имеется  конкретный  предел  численности  популяции, равный Х_мах, Ферхюльст положил R = r( Х_max - Х_n). С математической точки зрения удобнее выражать численность популяции в относительных единицах и положить R = r (1 - Х_n). Коэффициент пропорциональности r мы будем называть  управляющим параметром, или параметром  роста. Когда  r <  1,  численность  популяции  растет,  пока  не  достигнет  Х_max =  1,  при  котором  рост прекращается.  

Формула, описывающая изменения численности популяции, теперь будет следующий вид: 

                                                            X _n+1 = (1 + R) X_n - r Х_n² .                                       (6.4) 

Будем следить за эволюцией популяции на последующих шагах, то есть при увеличении n. На первый взгляд уравнение (6.4) достаточно простое и не предвещает  резких  перемен. Но  все  дело  в  нелинейности,  она  приводит  к сложным циклическим зависимостям, представленным на рис. 6.10. 



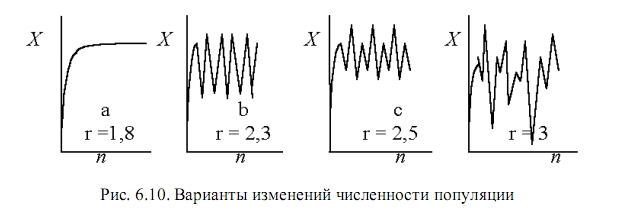
Для  области  значений  параметра  воспроизводства  от 0  до 1  численность популяции при любых начальных значениях все равно стремится к нулевому конечному уровню, физически это означает вымирание популяции. 

Когда параметр воспроизводства 1 < r < 2 , кривые роста плавно достигают  стационарного уровня, после чего каждый  год появляется новая популяция, точно замещающая предыдущую. 

При условии r = 2 происходит первая бифуркация, становятся возможными два варианта: численность популяции попеременно осциллирует между двумя уровнями. Прогноз развития достаточно определенный: после многих лет размножения мы встретим на острове либо высокий уровень численности насекомых, либо низкий. Объяснение можно дать простое: когда насекомых очень много, они истощают имеющиеся пищевые ресурсы и потомство оказывается в кризисных условиях перенаселения (по сравнению с малыми ресурсами). Наоборот, для малой численности при неистощенных ресурсах создаются благоприятные условия жизни и откладывается большое количество яиц, на будущий год потомство будет многочисленным. 

Когда  значения  параметра  воспроизводства  задаются (исследователем) большими  чем 2,449,  появляется  вторая бифуркация  и  теперь  численность  популяции  колеблется между  четырьмя  уровнями  значений.  Критические  значения параметра воспроизводства на  числовой оси лежат все ближе друг к другу, и при каждом из них происходит  разбиение на два уровня. В итоге прогноз развития популяции становится неопределенным, так как  становятся  возможными  самые  разные  значения для любого  года: от минимального  до  максимального.  В  таких случаях  говорят,  что  в  системе,  описываемой  уравнениями  типа (6.4),  устанавливается  динамический  хаос. Более подробно этот вопрос будет разбираться при выполнении компьютерных работ,  поэтому  здесь  отметим  лишь,  что  общее  представление  о  поведении многих  физических,  химических  и  биологических  нелинейных  систем,  подобных рассмотренной нами, может дать диаграмма Фейгенбаума. Конечно, для многих животных  коэффициент  прироста  популяции  равный 230%  или 250% не реален, однако для насекомых это не предел. 



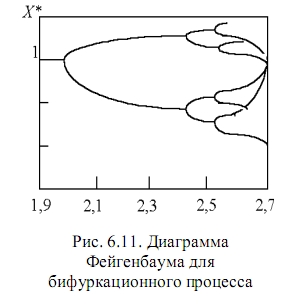
В 1963  г.  Э.Н.  Лоренц  обнаружил,  что  бифуркационное  поведение свойственно  турбулентному потоку.  Затем  оно  было  выявлено  в исследованиях  по  лазерной  физике  и  в  кинетике  химических  реакций.  В  настоящее время признано, что сценарий удвоения численности элементов нелинейных систем, их энергетических и структурных состояний является универсальным законом природы. Достаточно  сказать,  что  данная  закономерность проявляется  и  в  нелинейных  колебаниях  в  электрических  сетях (в  них могут  появляться  черты  детерминированного  хаоса),  и в  переходе  нормального  ритма сердца в угрожающую жизни человека фибрилляцию.
  
Существуют  и  другие  пути,  приводящие  к  появлению  динамического хаоса. В 1980  г. Б.Б. Мандельброт обнаружил, что существует более общий   153принцип перехода от порядка к хаосу, если от действительных значений некоторых управляющих параметров перейти в плоскость комплексных чисел. Процесс Мандельброта для дискретных изменений в принципе эквивалентен процессу Ферхюльста [13] : 

                                                                      X_n+1 = X ²_n + C,
  
где С - некоторая константа, могущая быть комплексным числом. 

Выберем  произвольное  число  Х0,  возведем  его  в  квадрат  и  прибавим константу С; полученное значение нанесем на комплексную плоскость. Затем повторим процесс - сделаем итерацию и отметим новое положение.  

При С = 0 имеются  три  типа  траекторий точки в зависимости от начального значения Х0. Если  оно  не  превосходит  единицу,  то  последующие квадраты будут  все меньше и меньше и  точка  стремится  к  нулю.  Говорят,  что  ноль является  аттрактором  для  итерационного  процесса.  Все  точки,  находящиеся  на  расстоянии меньше 1 от этого аттрактора движутся к нему. Наоборот,  все  точки  находящиеся  на  расстоянии больше 1 от ноля будут уходить на бесконечность,  так  как  значения  квадратов  будут только  возрастать. Наконец  точки, находящиеся  на  расстоянии 1  от  нуля  будут  оставаться неподвижными.  Окружность  единичного  радиуса является  границей между сферами влияния двух аттракторов - нуля и бесконечности.  



Когда  константой  C  является  комплексное число, то границы между несколькими (или очень  многими)  аттракторами  перестают  быть гладкими. Линия  границы выглядит непрерывно  изломанной,  причем  при  увеличении  масштаба графика во сколько угодно раз ее форма остается подобной себе. Такое свойство границ Мандельброт  назвал  фрактальной   структурой. Здесь  физические  процессы  хаотичны  до  предела,  так  как  совершается  переход  из  сферы влияния  одних  закономерностей  к  сфере  влияния другой. Отражая хаос, сама линия (множество  точек  которой  носит  название  множеств Жюлиа)  ок зывается эстетически  чень  красивой.  

Существует правило, указывающее, какой вид имеет множество Жюлиа для всех возможных  значений  параметра  С.  Графически  оно  выражается  множеством Мандельброта [13]. 
 
Компьютерное  моделирование  множеств  Жюлиа  позволило  сравнить их форму с формой многих естественных образований - морского берега, морозного узора на стекле, фигур электрических разрядов, формы ракушек, атмосферных  вихрей  и  других  форм  движения  или  результатов  физикохимических процессов.  

Как  оказалось,  наблюдается  поразительное  сходство  типов фигур,  несмотря  на  различие  конкретных  процессов  и  их  масштабов. Очевидно,  что единственная общая черта столь широкого круга процессов - их нелинейная динамика. Нелинейные процессы имеют фрактальные свойства. 



 

 
Концепции современного естествознания. Стародубцев В.А., 2-е изд., доп. — Томск.: Том. политех. ун-т, 2002. — 184 с. 

 
 

Содержание урока
 конспект урока
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%94%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D1%85%D0%B0%D0%BE%D1%81_%D0%B2_%D0%B8%D0%B7%D0%BE%D0%BB%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D0%BE%D0%B9_%D0%BF%D0%BE%D0%BF%D1%83%D0%BB%D1%8F%D1%86%D0%B8%D0%B8»
@@ Строка 5: / Строка 5: @@
 <br>
-<br>6.5. Динамический хаос в изолированной популяции <br><br>Будем&nbsp; рассматривать&nbsp; какую-нибудь&nbsp; изолированную&nbsp; популяцию,&nbsp; например популяцию насекомых на удаленном острове в открытом океане. Как известно, многие насекомые выводятся весной, лето живут, а осенью откладывают оплодотворенные яйца. При таком цикле воспроизводства поколения не перекрываются, все особи одного возраста. Говорят, что состояние популяции меняется дискретно во времени, поэтапно, одно за другим. Обозначим начальное&nbsp; состояние популяции через Хо,&nbsp; а Хn -&nbsp; её численность через n лет. Коэффициентом прироста R будем называть относительную величину изме-<br>нения численности популяции за год: &nbsp;<br><br>R =&nbsp; (Хn+1 - Хn)/Хn. Если считать R = const,&nbsp; то рост популяции будет определяться зависимостью (6.2) <br><br>X n+1 = (1 + R) Xn .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.2) <br><br>Через n лет численность популяции будет равна <br><br>Xn = (1 + R)n X0 .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.3) <br><br>Формула (6.3) предсказывает неограниченный рост популяции, что нереально.&nbsp; Чтобы&nbsp; быть&nbsp; ближе&nbsp; к&nbsp; действительной&nbsp; ситуации&nbsp; в&nbsp; биоценозах,&nbsp; П.Ф. Ферхюльст&nbsp; ещё&nbsp; в 1845&nbsp; г.&nbsp; постулировал,&nbsp; что&nbsp; коэффициент&nbsp; прироста R меняется в зависимости от достигнутой численности. Считая, что для данной экологической&nbsp; ниши&nbsp; имеется&nbsp; конкретный&nbsp; предел&nbsp; численности&nbsp; популяции, равный Хмах, Ферхюльст положил R = r( Хmax - Хn). С математической точки зрения удобнее выражать численность популяции в относительных единицах и положить R = r (1 - Хn). Коэффициент пропорциональности r мы будем называть&nbsp; управляющим параметром, или параметром&nbsp; роста. Когда&nbsp; r &lt;&nbsp; 1,&nbsp; численность&nbsp; популяции&nbsp; растет,&nbsp; пока&nbsp; не&nbsp; достигнет&nbsp; Хmax =&nbsp; 1,&nbsp; при&nbsp; котором&nbsp; рост <br>прекращается. &nbsp;<br><br>Формула, описывающая изменения численности популяции, теперь будет следующий вид: <br><br>X n+1 = (1 + R) Xn - r Хn2 .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.4) <br><br>Будем следить за эволюцией популяции на последующих шагах, то есть при увеличении n. На первый взгляд уравнение (6.4) достаточно простое и не предвещает&nbsp; резких&nbsp; перемен. Но&nbsp; все&nbsp; дело&nbsp; в&nbsp; нелинейности,&nbsp; она&nbsp; приводит&nbsp; к сложным циклическим зависимостям, представленным на рис. 6.10. <br><br>rfhn<br>&nbsp;<br>Рис. 6.10. Варианты изменений численности популяции &nbsp;<br><br>Для&nbsp; области&nbsp; значений&nbsp; параметра&nbsp; воспроизводства&nbsp; от 0&nbsp; до 1&nbsp; численность популяции при любых начальных значениях все равно стремится к нулевому конечному уровню, физически это означает вымирание популяции. <br><br>Когда параметр воспроизводства 1 &lt; r &lt; 2 , кривые роста плавно достигают&nbsp; стационарного уровня, после чего каждый&nbsp; год появляется новая популяция, точно замещающая предыдущую. <br><br>При условии r = 2 происходит первая бифуркация, становятся возможными два варианта: численность популяции попеременно осциллирует между двумя уровнями. Прогноз развития достаточно определенный: после многих лет размножения мы встретим на острове либо высокий уровень численности насекомых, либо низкий. Объяснение можно дать простое: когда насекомых очень много, они истощают имеющиеся пищевые ресурсы и потомство оказывается в кризисных условиях перенаселения (по сравнению с малыми ресурсами). Наоборот, для малой численности при неистощенных ресурсах создаются благоприятные условия жизни и откладывается большое количество яиц, на будущий год потомство будет многочисленным. <br><br>Когда&nbsp; значения&nbsp; параметра&nbsp; воспроизводства&nbsp; задаются (исследователем) большими&nbsp; чем 2,449,&nbsp; появляется&nbsp; вторая бифуркация&nbsp; и&nbsp; теперь&nbsp; численность&nbsp; популяции&nbsp; колеблется между&nbsp; четырьмя&nbsp; уровнями&nbsp; значений.&nbsp; Критические&nbsp; значения параметра воспроизводства на&nbsp; числовой оси лежат все ближе друг к другу, и при каждом из них происходит&nbsp; разбиение на два уровня. В итоге прогноз развития популяции становится неопределенным, так как&nbsp; становятся&nbsp; возможными&nbsp; самые&nbsp; разные&nbsp; значения для любого&nbsp; года: от минимального&nbsp; до&nbsp; максимального.&nbsp; В&nbsp; таких случаях&nbsp; говорят,&nbsp; что&nbsp; в&nbsp; системе,&nbsp; описываемой&nbsp; уравнениями&nbsp; типа (6.4),&nbsp; устанавливается&nbsp; динамический&nbsp; хаос. Более подробно этот вопрос будет разбираться при выполнении компьютерных работ,&nbsp; поэтому&nbsp; здесь&nbsp; отметим&nbsp; лишь,&nbsp; что&nbsp; общее&nbsp; представление&nbsp; о&nbsp; поведении многих&nbsp; физических,&nbsp; химических&nbsp; и&nbsp; биологических&nbsp; нелинейных&nbsp; систем,&nbsp; подобных рассмотренной нами, может дать диаграмма Фейгенбаума. Конечно, для многих животных&nbsp; коэффициент&nbsp; прироста&nbsp; популяции&nbsp; равный 230%&nbsp; или 250% не реален, однако для насекомых это не предел. <br><br>rfhn<br><br>Рис. 6.11. Диаграмма&nbsp; Фейгенбаума для&nbsp; бифуркационного процесса <br><br>В 1963&nbsp; г.&nbsp; Э.Н.&nbsp; Лоренц&nbsp; обнаружил,&nbsp; что&nbsp; бифуркационное&nbsp; поведение свойственно&nbsp; турбулентному потоку.&nbsp; Затем&nbsp; оно&nbsp; было&nbsp; выявлено&nbsp; в исследованиях&nbsp; по&nbsp; лазерной&nbsp; физике&nbsp; и&nbsp; в&nbsp; кинетике&nbsp; химических&nbsp; реакций.&nbsp; В&nbsp; настоящее время признано, что сценарий удвоения численности элементов нелинейных систем, их энергетических и структурных состояний является универсальным законом природы. Достаточно&nbsp; сказать,&nbsp; что&nbsp; данная&nbsp; закономерность проявляется&nbsp; и&nbsp; в&nbsp; нелинейных&nbsp; колебаниях&nbsp; в&nbsp; электрических&nbsp; сетях (в&nbsp; них могут&nbsp; появляться&nbsp; черты&nbsp; детерминированного&nbsp; хаоса),&nbsp; и в&nbsp; переходе&nbsp; нормального&nbsp; ритма сердца в угрожающую жизни человека фибрилляцию.<br>&nbsp; <br>Существуют&nbsp; и&nbsp; другие&nbsp; пути,&nbsp; приводящие&nbsp; к&nbsp; появлению&nbsp; динамического хаоса. В 1980&nbsp; г. Б.Б. Мандельброт обнаружил, что существует более общий&nbsp;&nbsp; 153принцип перехода от порядка к хаосу, если от действительных значений некоторых управляющих параметров перейти в плоскость комплексных чисел. Процесс Мандельброта для дискретных изменений в принципе эквивалентен процессу Ферхюльста [13] : <br><br>&nbsp;Xn+1 = X 2n + C,<br>&nbsp; <br>где С - некоторая константа, могущая быть комплексным числом. <br><br>Выберем&nbsp; произвольное&nbsp; число&nbsp; Х0,&nbsp; возведем&nbsp; его&nbsp; в&nbsp; квадрат&nbsp; и&nbsp; прибавим константу С; полученное значение нанесем на комплексную плоскость. Затем повторим процесс - сделаем итерацию и отметим новое положение. &nbsp;<br><br>При С = 0 имеются&nbsp; три&nbsp; типа&nbsp; траекторий точки в зависимости от начального значения Х0. Если&nbsp; оно&nbsp; не&nbsp; превосходит&nbsp; единицу,&nbsp; то&nbsp; последующие квадраты будут&nbsp; все меньше и меньше и&nbsp; точка&nbsp; стремится&nbsp; к&nbsp; нулю.&nbsp; Говорят,&nbsp; что&nbsp; ноль является&nbsp; аттрактором&nbsp; для&nbsp; итерационного&nbsp; процесса.&nbsp; Все&nbsp; точки,&nbsp; находящиеся&nbsp; на&nbsp; расстоянии меньше 1 от этого аттрактора движутся к нему. Наоборот,&nbsp; все&nbsp; точки&nbsp; находящиеся&nbsp; на&nbsp; расстоянии больше 1 от ноля будут уходить на бесконечность,&nbsp; так&nbsp; как&nbsp; значения&nbsp; квадратов&nbsp; будут только&nbsp; возрастать. Наконец&nbsp; точки, находящиеся&nbsp; на&nbsp; расстоянии 1&nbsp; от&nbsp; нуля&nbsp; будут&nbsp; оставаться неподвижными.&nbsp; Окружность&nbsp; единичного&nbsp; радиуса является&nbsp; границей между сферами влияния двух аттракторов - нуля и бесконечности. &nbsp;<br><br>rfhn<br>Рис. 6.12. Форма бассейна для аттрактора в точке 0 <br>Рис. 6.14. Форма множества Мандельброта<br>Рис. 6.13. Форма части&nbsp; множества Жюлиа <br><br>Когда&nbsp; константой&nbsp; C&nbsp; является&nbsp; комплексное число, то границы между несколькими (или <br>очень&nbsp; многими)&nbsp; аттракторами&nbsp; перестают&nbsp; быть гладкими. Линия&nbsp; границы выглядит непрерывно&nbsp; изломанной,&nbsp; причем&nbsp; при&nbsp; увеличении&nbsp; масштаба графика во сколько угодно раз ее форма остается подобной себе. Такое свойство границ Мандельброт&nbsp; назвал&nbsp; фрактальной&nbsp;&nbsp; структурой. Здесь&nbsp; физические&nbsp; процессы&nbsp; хаотичны&nbsp; до&nbsp; предела,&nbsp; так&nbsp; как&nbsp; совершается&nbsp; переход&nbsp; из&nbsp; сферы влияния&nbsp; одних&nbsp; закономерностей&nbsp; к&nbsp; сфере&nbsp; влияния другой. Отражая хаос, сама линия (множество&nbsp; точек&nbsp; которой&nbsp; носит&nbsp; название&nbsp; множеств Жюлиа)&nbsp; ок зывается эстетически&nbsp; чень&nbsp; красивой. &nbsp;<br><br>Существует правило, указывающее, какой вид имеет множество Жюлиа для всех возможных&nbsp; значений&nbsp; параметра&nbsp; С.&nbsp; Графически&nbsp; оно&nbsp; выражается&nbsp; множеством Мандельброта [13]. <br>&nbsp;<br>Компьютерное&nbsp; моделирование&nbsp; множеств&nbsp; Жюлиа&nbsp; позволило&nbsp; сравнить их форму с формой многих естественных образований - морского берега, морозного узора на стекле, фигур электрических разрядов, формы ракушек, атмосферных&nbsp; вихрей&nbsp; и&nbsp; других&nbsp; форм&nbsp; движения&nbsp; или&nbsp; результатов&nbsp; физикохимических процессов. &nbsp;<br><br>Как&nbsp; оказалось,&nbsp; наблюдается&nbsp; поразительное&nbsp; сходство&nbsp; типов фигур,&nbsp; несмотря&nbsp; на&nbsp; различие&nbsp; конкретных&nbsp; процессов&nbsp; и&nbsp; их&nbsp; масштабов. Очевидно,&nbsp; что единственная общая черта столь широкого круга процессов - их нелинейная динамика. Нелинейные процессы имеют фрактальные свойства. <br><br><br><br>
+<br>'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; 6.5. Динамический хаос в изолированной популяции '''<br><br>Будем&nbsp; рассматривать&nbsp; какую-нибудь&nbsp; изолированную&nbsp; популяцию,&nbsp; например популяцию насекомых на удаленном острове в открытом океане. Как известно, многие насекомые выводятся весной, лето живут, а осенью откладывают оплодотворенные яйца. При таком цикле воспроизводства поколения не перекрываются, все особи одного возраста. Говорят, что состояние популяции меняется дискретно во времени, поэтапно, одно за другим. Обозначим начальное&nbsp; состояние популяции через Х<sub>о</sub>,&nbsp; а Х<sub>n</sub> -&nbsp; её численность через n лет. Коэффициентом прироста R будем называть относительную величину изменения численности популяции за год: &nbsp;<br><br>R =&nbsp; (Х<sub>n+1</sub> - Х<sub>n</sub>)/Х<sub>n</sub>. Если считать R =''const'',&nbsp; то рост популяции будет определяться зависимостью (6.2) <br><br>'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; X <sub>n+1</sub> = (1 + R) X<sub>n</sub> .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.2) '''<br><br>Через n лет численность популяции будет равна <br>'''<br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; X<sub>n</sub> = (1 + R)<sub>n</sub> X<sub>0</sub> .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.3) '''<br><br>Формула (6.3) предсказывает неограниченный рост популяции, что нереально.&nbsp; Чтобы&nbsp; быть&nbsp; ближе&nbsp; к&nbsp; действительной&nbsp; ситуации&nbsp; в&nbsp; биоценозах,&nbsp; П.Ф. Ферхюльст&nbsp; ещё&nbsp; в 1845&nbsp; г.&nbsp; постулировал,&nbsp; что&nbsp; коэффициент&nbsp; прироста R меняется в зависимости от достигнутой численности. Считая, что для данной экологической&nbsp; ниши&nbsp; имеется&nbsp; конкретный&nbsp; предел&nbsp; численности&nbsp; популяции, равный Х<sub>мах</sub>, Ферхюльст положил R = r( Х<sub>max</sub> - Х<sub>n</sub>). С математической точки зрения удобнее выражать численность популяции в относительных единицах и положить R = r (1 - Х<sub>n</sub>). Коэффициент пропорциональности r мы будем называть&nbsp; управляющим параметром, или параметром&nbsp; роста. Когда&nbsp; r &lt;&nbsp; 1,&nbsp; численность&nbsp; популяции&nbsp; растет,&nbsp; пока&nbsp; не&nbsp; достигнет&nbsp; Х<sub>max</sub> =&nbsp; 1,&nbsp; при&nbsp; котором&nbsp; рост прекращается. &nbsp;<br><br>Формула, описывающая изменения численности популяции, теперь будет следующий вид: <br><br>'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; X <sub>n+1</sub> = (1 + R) X<sub>n</sub> - r Х<sub>n</sub><sup>2</sup> .&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (6.4) '''<br><br>Будем следить за эволюцией популяции на последующих шагах, то есть при увеличении n. На первый взгляд уравнение (6.4) достаточно простое и не предвещает&nbsp; резких&nbsp; перемен. Но&nbsp; все&nbsp; дело&nbsp; в&nbsp; нелинейности,&nbsp; она&nbsp; приводит&nbsp; к сложным циклическим зависимостям, представленным на рис. 6.10.
+<br>[[Image:1-03-01.jpg]]<br><br>Для&nbsp; области&nbsp; значений&nbsp; параметра&nbsp; воспроизводства&nbsp; от 0&nbsp; до 1&nbsp; численность популяции при любых начальных значениях все равно стремится к нулевому конечному уровню, физически это означает вымирание популяции. <br><br>Когда параметр воспроизводства 1 &lt; r &lt; 2 , кривые роста плавно достигают&nbsp; стационарного уровня, после чего каждый&nbsp; год появляется новая популяция, точно замещающая предыдущую. <br><br>При условии r = 2 происходит первая бифуркация, становятся возможными два варианта: численность популяции попеременно осциллирует между двумя уровнями. Прогноз развития достаточно определенный: после многих лет размножения мы встретим на острове либо высокий уровень численности насекомых, либо низкий. Объяснение можно дать простое: когда насекомых очень много, они истощают имеющиеся пищевые ресурсы и потомство оказывается в кризисных условиях перенаселения (по сравнению с малыми ресурсами). Наоборот, для малой численности при неистощенных ресурсах создаются благоприятные условия жизни и откладывается большое количество яиц, на будущий год потомство будет многочисленным. <br><br>Когда&nbsp; значения&nbsp; параметра&nbsp; воспроизводства&nbsp; задаются (исследователем) большими&nbsp; чем 2,449,&nbsp; появляется&nbsp; вторая бифуркация&nbsp; и&nbsp; теперь&nbsp; численность&nbsp; популяции&nbsp; колеблется между&nbsp; четырьмя&nbsp; уровнями&nbsp; значений.&nbsp; Критические&nbsp; значения параметра воспроизводства на&nbsp; числовой оси лежат все ближе друг к другу, и при каждом из них происходит&nbsp; разбиение на два уровня. В итоге прогноз развития популяции становится неопределенным, так как&nbsp; становятся&nbsp; возможными&nbsp; самые&nbsp; разные&nbsp; значения для любого&nbsp; года: от минимального&nbsp; до&nbsp; максимального.&nbsp; В&nbsp; таких случаях&nbsp; говорят,&nbsp; что&nbsp; в&nbsp; системе,&nbsp; описываемой&nbsp; уравнениями&nbsp; типа (6.4),&nbsp; устанавливается&nbsp; динамический&nbsp; хаос. Более подробно этот вопрос будет разбираться при выполнении компьютерных работ,&nbsp; поэтому&nbsp; здесь&nbsp; отметим&nbsp; лишь,&nbsp; что&nbsp; общее&nbsp; представление&nbsp; о&nbsp; поведении многих&nbsp; физических,&nbsp; химических&nbsp; и&nbsp; биологических&nbsp; нелинейных&nbsp; систем,&nbsp; подобных рассмотренной нами, может дать диаграмма Фейгенбаума. Конечно, для многих животных&nbsp; коэффициент&nbsp; прироста&nbsp; популяции&nbsp; равный 230%&nbsp; или 250% не реален, однако для насекомых это не предел.
+<br>[[Image:1-03-02.jpg]]<br><br>В 1963&nbsp; г.&nbsp; Э.Н.&nbsp; Лоренц&nbsp; обнаружил,&nbsp; что&nbsp; бифуркационное&nbsp; поведение свойственно&nbsp; турбулентному потоку.&nbsp; Затем&nbsp; оно&nbsp; было&nbsp; выявлено&nbsp; в исследованиях&nbsp; по&nbsp; лазерной&nbsp; физике&nbsp; и&nbsp; в&nbsp; кинетике&nbsp; химических&nbsp; реакций.&nbsp; В&nbsp; настоящее время признано, что сценарий удвоения численности элементов нелинейных систем, их энергетических и структурных состояний является универсальным законом природы. Достаточно&nbsp; сказать,&nbsp; что&nbsp; данная&nbsp; закономерность проявляется&nbsp; и&nbsp; в&nbsp; нелинейных&nbsp; колебаниях&nbsp; в&nbsp; электрических&nbsp; сетях (в&nbsp; них могут&nbsp; появляться&nbsp; черты&nbsp; детерминированного&nbsp; хаоса),&nbsp; и в&nbsp; переходе&nbsp; нормального&nbsp; ритма сердца в угрожающую жизни человека фибрилляцию.<br>&nbsp; <br>Существуют&nbsp; и&nbsp; другие&nbsp; пути,&nbsp; приводящие&nbsp; к&nbsp; появлению&nbsp; динамического хаоса. В 1980&nbsp; г. Б.Б. Мандельброт обнаружил, что существует более общий&nbsp;&nbsp; 153принцип перехода от порядка к хаосу, если от действительных значений некоторых управляющих параметров перейти в плоскость комплексных чисел. Процесс Мандельброта для дискретных изменений в принципе эквивалентен процессу Ферхюльста [13]&nbsp;: <br>'''<br>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; X<sub>n+1</sub> = X <sup>2</sup><sub>n</sub> + C,'''<br>&nbsp; <br>где С - некоторая константа, могущая быть комплексным числом. <br><br>Выберем&nbsp; произвольное&nbsp; число&nbsp; Х0,&nbsp; возведем&nbsp; его&nbsp; в&nbsp; квадрат&nbsp; и&nbsp; прибавим константу С; полученное значение нанесем на комплексную плоскость. Затем повторим процесс - сделаем итерацию и отметим новое положение. &nbsp;<br><br>При С = 0 имеются&nbsp; три&nbsp; типа&nbsp; траекторий точки в зависимости от начального значения Х0. Если&nbsp; оно&nbsp; не&nbsp; превосходит&nbsp; единицу,&nbsp; то&nbsp; последующие квадраты будут&nbsp; все меньше и меньше и&nbsp; точка&nbsp; стремится&nbsp; к&nbsp; нулю.&nbsp; Говорят,&nbsp; что&nbsp; ноль является&nbsp; аттрактором&nbsp; для&nbsp; итерационного&nbsp; процесса.&nbsp; Все&nbsp; точки,&nbsp; находящиеся&nbsp; на&nbsp; расстоянии меньше 1 от этого аттрактора движутся к нему. Наоборот,&nbsp; все&nbsp; точки&nbsp; находящиеся&nbsp; на&nbsp; расстоянии больше 1 от ноля будут уходить на бесконечность,&nbsp; так&nbsp; как&nbsp; значения&nbsp; квадратов&nbsp; будут только&nbsp; возрастать. Наконец&nbsp; точки, находящиеся&nbsp; на&nbsp; расстоянии 1&nbsp; от&nbsp; нуля&nbsp; будут&nbsp; оставаться неподвижными.&nbsp; Окружность&nbsp; единичного&nbsp; радиуса является&nbsp; границей между сферами влияния двух аттракторов - нуля и бесконечности. &nbsp;<br><br>[[Image:1-03-03.jpg]]<br><br>Когда&nbsp; константой&nbsp; C&nbsp; является&nbsp; комплексное число, то границы между несколькими (или очень&nbsp; многими)&nbsp; аттракторами&nbsp; перестают&nbsp; быть гладкими. Линия&nbsp; границы выглядит непрерывно&nbsp; изломанной,&nbsp; причем&nbsp; при&nbsp; увеличении&nbsp; масштаба графика во сколько угодно раз ее форма остается подобной себе. Такое свойство границ Мандельброт&nbsp; назвал&nbsp; фрактальной&nbsp;&nbsp; структурой. Здесь&nbsp; физические&nbsp; процессы&nbsp; хаотичны&nbsp; до&nbsp; предела,&nbsp; так&nbsp; как&nbsp; совершается&nbsp; переход&nbsp; из&nbsp; сферы влияния&nbsp; одних&nbsp; закономерностей&nbsp; к&nbsp; сфере&nbsp; влияния другой. Отражая хаос, сама линия (множество&nbsp; точек&nbsp; которой&nbsp; носит&nbsp; название&nbsp; множеств Жюлиа)&nbsp; ок зывается эстетически&nbsp; чень&nbsp; красивой. &nbsp;<br><br>Существует правило, указывающее, какой вид имеет множество Жюлиа для всех возможных&nbsp; значений&nbsp; параметра&nbsp; С.&nbsp; Графически&nbsp; оно&nbsp; выражается&nbsp; множеством Мандельброта [13]. <br>&nbsp;<br>Компьютерное&nbsp; моделирование&nbsp; множеств&nbsp; Жюлиа&nbsp; позволило&nbsp; сравнить их форму с формой многих естественных образований - морского берега, морозного узора на стекле, фигур электрических разрядов, формы ракушек, атмосферных&nbsp; вихрей&nbsp; и&nbsp; других&nbsp; форм&nbsp; движения&nbsp; или&nbsp; результатов&nbsp; физикохимических процессов. &nbsp;<br><br>Как&nbsp; оказалось,&nbsp; наблюдается&nbsp; поразительное&nbsp; сходство&nbsp; типов фигур,&nbsp; несмотря&nbsp; на&nbsp; различие&nbsp; конкретных&nbsp; процессов&nbsp; и&nbsp; их&nbsp; масштабов. Очевидно,&nbsp; что единственная общая черта столь широкого круга процессов - их нелинейная динамика. Нелинейные процессы имеют фрактальные свойства. <br><br><br><br>
 <br>

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: