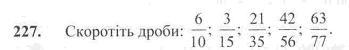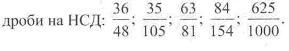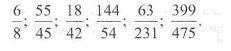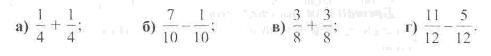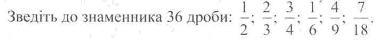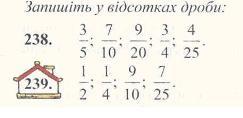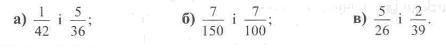|
|
|
| Строка 5: |
Строка 5: |
| | [[Image:Qm28.jpg]] | | [[Image:Qm28.jpg]] |
| | | | |
| - | Ділення чисельника і знаменника дробу на їх спільний діль¬ник, відмінний від одиниці, називають скороченням дробу.<br>Найбільшим числом, на яке можна скоротити дріб, є найбільший спіль¬ний дільник чисельника і знаменника.<br>Дріб 4/5 скоротити не можна. Такий дріб називають нескоротним. Чисель¬ник і знаменник нескоротного дробу є взаємно простими числами.<br>б) Зведення дробу до нового знаменника<br>З<br>Використавши основну властивість дробу, дріб — можна записати дро¬бом зі знаменником 12, помноживши його чисельник і знаменник на 3:<br>[[Image:Qm29.jpg]] | + | Ділення чисельника і знаменника дробу на їх спільний дільник, відмінний від одиниці, називають скороченням дробу.<br>Найбільшим числом, на яке можна скоротити дріб, є найбільший спільний дільник чисельника і знаменника.<br>Дріб 4/5 скоротити не можна. Такий дріб називають нескоротним. Чисельник і знаменник нескоротного дробу є взаємно простими числами.<br>б) Зведення дробу до нового знаменника<br>З<br>Використавши основну властивість дробу, дріб — можна записати дробом зі знаменником 12, помноживши його чисельник і знаменник на 3:<br>[[Image:Qm29.jpg]] |
| | | | |
| - | Прочитайте<br><br>1. Скоротити дріб 24/60<br>• Скорочення можна проводити поступово, використовуючи, по можли¬вості, ознаки подільності: | + | Прочитайте<br><br>1. Скоротити дріб 24/60<br>• Скорочення можна проводити поступово, використовуючи, по можливості, ознаки подільності: |
| | | | |
| | [[Image:Qm30.jpg]] | | [[Image:Qm30.jpg]] |
| Строка 41: |
Строка 41: |
| | Рівень Б<br>240. Запишіть звичайним нескоротним дробом:<br>[[Image:Qm41.jpg]] | | Рівень Б<br>240. Запишіть звичайним нескоротним дробом:<br>[[Image:Qm41.jpg]] |
| | | | |
| - | 241<br>Виразіть у кілограмах і запишіть звичайним нескоротним дробом: 25 г; 125 г; 250 г; 160 г; 825 г; 950 г.<br>242. Виразіть у кілограмах і запишіть мішаним числом з нескоротною дробо¬вою частиною: 3125 г; 15 500 г; 18 375 г; 7 кг 150 г.<br>243. Виразіть у годинах і запишіть мішаним числом з нескоротною дробовою частиною: 90 хв; 130 хв; 270 хв; 310 хв; 5 год 12 хв.<br><br>245. Сума чисельника і знаменника дробу дорівнює 48. Після скорочення цього дробу одержали 3/5 . Знайдіть початковий дріб.<br>246<br>Наталя записала дріб, різниця знаменника і чисельника якого дорівнює<br><br>15. після скорочення дробу вона отримала 2/7. Який початковий дріб записала Наталя?<br>Здогадайтеся<br>247. Аркуш паперу розріжемо на 8 або на 12 частин. Далі деякі з частин знову розріжемо на 8, а деякі — на 12 частин. Чи можна, продовжуючи розрізування у такий спосіб, отримати 44 частини з цього аркуша?<br>Вправи для повторення<br>248. Знайдіть НСК знаменників дробів:<br>[[Image:Qm42.jpg]] | + | 241<br>Виразіть у кілограмах і запишіть звичайним нескоротним дробом: 25 г; 125 г; 250 г; 160 г; 825 г; 950 г.<br>242. Виразіть у кілограмах і запишіть мішаним числом з нескоротною дробовою частиною: 3125 г; 15 500 г; 18 375 г; 7 кг 150 г.<br>243. Виразіть у годинах і запишіть мішаним числом з нескоротною дробовою частиною: 90 хв; 130 хв; 270 хв; 310 хв; 5 год 12 хв.<br><br>245. Сума чисельника і знаменника дробу дорівнює 48. Після скорочення цього дробу одержали 3/5 . Знайдіть початковий дріб.<br>246<br>Наталя записала дріб, різниця знаменника і чисельника якого дорівнює<br><br>15. після скорочення дробу вона отримала 2/7. Який початковий дріб записала Наталя?<br>Здогадайтеся<br>247. Аркуш паперу розріжемо на 8 або на 12 частин. Далі деякі з частин знову розріжемо на 8, а деякі — на 12 частин. Чи можна, продовжуючи розрізування у такий спосіб, отримати 44 частини з цього аркуша?<br>Вправи для повторення<br>248. Знайдіть НСК знаменників дробів:<br>[[Image:Qm42.jpg]] |
| | | | |
| | [[Image:Qm43.jpg]] | | [[Image:Qm43.jpg]] |
Версия 09:02, 16 марта 2010
Гіпермаркет Знань>>Математика>>Математика 6 клас>> Математика: Тема 2.ДОДАВАННЯ 1 ВІДНІМАННЯ ЗВИЧАЙНИХ ДРОБІВ . . Застосування основної властивості дробу
1.
а) Скорочення дробу
Використавши основну властивість дробу, іноді можна замінити один дріб іншим, який дорівнює йому, але з меншими чисельником і знаменником.

Ділення чисельника і знаменника дробу на їх спільний дільник, відмінний від одиниці, називають скороченням дробу.
Найбільшим числом, на яке можна скоротити дріб, є найбільший спільний дільник чисельника і знаменника.
Дріб 4/5 скоротити не можна. Такий дріб називають нескоротним. Чисельник і знаменник нескоротного дробу є взаємно простими числами.
б) Зведення дробу до нового знаменника
З
Використавши основну властивість дробу, дріб — можна записати дробом зі знаменником 12, помноживши його чисельник і знаменник на 3:

Прочитайте
1. Скоротити дріб 24/60
• Скорочення можна проводити поступово, використовуючи, по можливості, ознаки подільності:

Скорочення можна проводити, поділивши чисельник і знаменник на їх НСД. Оскільки НСД(24; 60) = 12, то

Усно

Рівень А

228. Запишіть усі правильні дроби зі знаменником 12. Скоротіть з них ті, які можна скоротити.
229
Запишіть усі правильні дроби зі знаменником 20. Скоротіть з них ті, які можна скоротити.
230. Знайдіть НСД чисельника і знаменника кожного із дробів та скоротіть
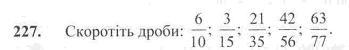
231. Скоротіть неправильні дроби та виділіть їх цілі частини:
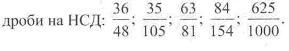
232
Скоротіть дроби та виділіть для неправильних дробів їх цілі частини:
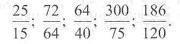
Запишіть звичайними нескоротними дробами: 233. 0,4; 0,25; 0,05; 0,08; 0,65; 0,625; 75%; 16%.
234.
0,5; 0,8; 0,125; 0,24; 0,875; 85%; 32%.
235. Виконайте дію і результат запишіть нескоротним дробом:
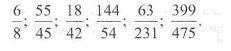
236. Зведіть до знаменника 48 дроби:
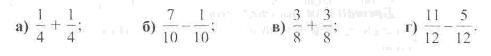
237
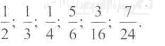
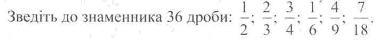
Рівень Б
240. Запишіть звичайним нескоротним дробом:
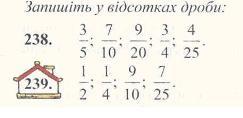
241
Виразіть у кілограмах і запишіть звичайним нескоротним дробом: 25 г; 125 г; 250 г; 160 г; 825 г; 950 г.
242. Виразіть у кілограмах і запишіть мішаним числом з нескоротною дробовою частиною: 3125 г; 15 500 г; 18 375 г; 7 кг 150 г.
243. Виразіть у годинах і запишіть мішаним числом з нескоротною дробовою частиною: 90 хв; 130 хв; 270 хв; 310 хв; 5 год 12 хв.
245. Сума чисельника і знаменника дробу дорівнює 48. Після скорочення цього дробу одержали 3/5 . Знайдіть початковий дріб.
246
Наталя записала дріб, різниця знаменника і чисельника якого дорівнює
15. після скорочення дробу вона отримала 2/7. Який початковий дріб записала Наталя?
Здогадайтеся
247. Аркуш паперу розріжемо на 8 або на 12 частин. Далі деякі з частин знову розріжемо на 8, а деякі — на 12 частин. Чи можна, продовжуючи розрізування у такий спосіб, отримати 44 частини з цього аркуша?
Вправи для повторення
248. Знайдіть НСК знаменників дробів:
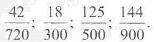
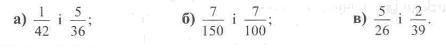
250. Один ковзаняр пробігає коло за 36 с, а інший — за 42 с. Через скільки секунд після спільного старту ковзанярі знову зустрінуться на стартовій позначці?
251. Використовуючи цифри 1, 2, 3, 5, 8 не більше одного разу, запишіть чотирицифрове число, яке ділилося б на 5 і на 9.
252. У школі навчається 560 учнів, 25% усіх учнів навчається у старших класах, 45% решти — у середніх класах. Скільки учнів навчається у молодших класах?
Онлайн-бібліотека з підручниками і книгами, тести з математики, завдання з математики 6 клас, календарне планування
Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту
 конспект уроку і опорний каркас конспект уроку і опорний каркас
 презентація уроку презентація уроку
 акселеративні методи та інтерактивні технології акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями) закриті вправи (тільки для використання вчителями)
 оцінювання
Практика оцінювання
Практика
 задачі та вправи,самоперевірка задачі та вправи,самоперевірка
 практикуми, лабораторні, кейси практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання
Ілюстрації домашнє завдання
Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати реферати
 фішки для допитливих фішки для допитливих
 шпаргалки шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення
 зовнішнє незалежне тестування (ЗНТ) зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні підручники основні і допоміжні
 тематичні свята, девізи тематичні свята, девізи
 статті статті
 національні особливості національні особливості
 словник термінів словник термінів
 інше
Тільки для вчителів інше
Тільки для вчителів
 ідеальні уроки ідеальні уроки
 календарний план на рік календарний план на рік
 методичні рекомендації методичні рекомендації
 програми програми
 обговорення обговорення
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|