|
|
|
| Строка 3: |
Строка 3: |
| | Метеорологи вимірювали температуру повітря протягом першої половини доби і результати записали до таблиці:<br> | | Метеорологи вимірювали температуру повітря протягом першої половини доби і результати записали до таблиці:<br> |
| | | | |
| - | [[Image:asd343.jpg]] | + | [[Image:Asd343.jpg]] |
| | | | |
| - | Потім вони вирішили нанести результати вимірювання на координатну площину, відклавши на осі абсцис значення часу (7, год), а на осі ординат — значення температури (Т, °С). Було позначено 13 точок: (0; -2), (1; -3,5), (12; 6). Абсциса кожної з цих точок — це значення часу, а ордината — значення температури повітря у цей час. Якби метеорологи вимірювали температуру щопівгодини і результати вимірювання наносили на координатну площину, то точки знаходилися б ближче одна до одної. Якби вимірювання проводилося щочверть години, то точки на координатній площині були б розміщені ще густіше і т. д.<br>Якщо точки, побудовані таким чином на координатній площині, сполучити плавною лінією, то одержимо фігуру, яку називають графіком залежності температури повітря від часу (рис. 78).<br>[[Image:asd344.jpg]]<br> | + | Потім вони вирішили нанести результати вимірювання на координатну площину, відклавши на осі абсцис значення часу (7, год), а на осі ординат — значення температури (Т, °С). Було позначено 13 точок: (0; -2), (1; -3,5), (12; 6). Абсциса кожної з цих точок — це значення часу, а ордината — значення температури повітря у цей час. Якби метеорологи вимірювали температуру щопівгодини і результати вимірювання наносили на координатну площину, то точки знаходилися б ближче одна до одної. Якби вимірювання проводилося щочверть години, то точки на координатній площині були б розміщені ще густіше і т. д.<br>Якщо точки, побудовані таким чином на координатній площині, сполучити плавною лінією, то одержимо фігуру, яку називають графіком залежності температури повітря від часу (рис. 78).<br>[[Image:Asd344.jpg]]<br> |
| | | | |
| - | Розглянемо ще такі приклади.<br>1. Туристові потрібно пройти 12 км. Він вирахував час руху залежно від швидкості, з якою йтиме, й одержав таку таблицю:<br>[[Image:asd345.jpg]] | + | Розглянемо ще такі приклади.<br>1. Туристові потрібно пройти 12 км. Він вирахував час руху залежно від швидкості, з якою йтиме, й одержав таку таблицю:<br>[[Image:Asd345.jpg]] |
| | | | |
| - | Побудуємо на координатній площині точки за цією таблицею, відклавши на осі абсцис значення швидкості (v, км/год), а на осі ординат — значення часу (і, год).<br>Сполучивши плавною лінією побудовані точки, одержимо графік залежності часу від швидкості за сталої відстані (12 км) (рис. 79).<br>[[Image:asd346.jpg]] | + | Побудуємо на координатній площині точки за цією таблицею, відклавши на осі абсцис значення швидкості (v, км/год), а на осі ординат — значення часу (і, год).<br>Сполучивши плавною лінією побудовані точки, одержимо графік залежності часу від швидкості за сталої відстані (12 км) (рис. 79).<br>[[Image:Asd346.jpg]] |
| | | | |
| - | Цю залежність часу t (у год) від швидкості u (у км/год), можна задати 12<br>формулою t = 12/u .<br><br>2, Відомо, що до басейну щосекунди вливається 0,5 м<sup>3</sup> води. Потрібно знайти, скільки буде води в басейні через t с.<br>Залежність об'єму води У(у м<sup>3</sup><sup></sup>) від часу / (у секундах) можна задати формулою V= 0,5?.<br>Надамо / певних значень, знайдемо відповідні значення об'єму води в басейні і результати занесемо до таблиці:<br>[[Image:asd347.jpg]] | + | Цю залежність часу t (у год) від швидкості u (у км/год), можна задати 12<br>формулою t = 12/u .<br><br>2, Відомо, що до басейну щосекунди вливається 0,5 м<sup>3</sup> води. Потрібно знайти, скільки буде води в басейні через t с.<br>Залежність об'єму води У(у м<sup>3</sup><sup></sup>) від часу / (у секундах) можна задати формулою V= 0,5?.<br>Надамо / певних значень, знайдемо відповідні значення об'єму води в басейні і результати занесемо до таблиці:<br>[[Image:Asd347.jpg]] |
| | | | |
| - | За даними таблиці побудуємо на координатній площині точки, відклавши на осі абсцис значення часу (і, с), а на осі ординат — значення об'єму (V, м<sup>3</sup>). | + | За даними таблиці побудуємо на координатній площині точки, відклавши на осі абсцис значення часу (і, с), а на осі ординат — значення об'єму (V, м<sup>3</sup>). |
| | | | |
| - | [[Image:asd348.jpg]] | + | [[Image:Asd348.jpg]] |
| | | | |
| - | Рис. 80<br>Приклавши лінійку до побудованих точок, бачимо, що вони лежать на одній прямій. Сполучивши крайні точки відрізком, одержимо графік залежності об'єму води в басейні від часу його наповнення.<br><br>Прочитайте<br><br>1. Користуючись графіком залежності об'єму води в басейні від часу його наповнення (рис. 80), знайти: а) об'єм, якщо 1= 13; б) час, якщо V=6. • а) На осі абсцис, на якій відкладали час І, позначаємо точку з абсцисою 13, проводимо через неї пряму, перпендикулярну до осі абсцис, та знаходимо точку перетину прямої з графіком. Через одержану на графіку точку проводимо<br> <br>пряму, перпендикулярну до осі ординат, на якій відкладали об'єм. Ордината точки перетину цієї прямої з віссю ординат дорівнює значенню об'єму: V= 6,5.<br>б) На осі ординат, на якій відкладали об'єм V, позначаємо точку з ординатою 6, будуємо перпендикулярну пряму та знаходимо точку її перетину з графіком. Через одержану на графіку точку проводимо пряму, перпендикулярну до осі абсцис, на якій відкладали час. Абсциса точки перетину цієї прямої та осі абсцис дорівнює значенню часу: 1= 12. •<br><br>Усно<br>1354. Автомобіль рухається зі швидкістю 80 км/год. Який шлях проїде автомобіль за 0,5 год; 1 год; 2 год; 2,5 год? За якою формулою можна обчислити шлях 5 (у км), пройдений автомобілем за час і (у год)?<br>1355. Площа прямокутника дорівнює 18 см2. Чому дорівнює сторона прямокутника, якщо інша його сторона дорівнює 3 см; 6 см; 36 см? За якою формулою можна обчислити сторону b (у см) прямокутника, знаючи довжину а (у см) іншої його сторони?<br> | + | Рис. 80<br>Приклавши лінійку до побудованих точок, бачимо, що вони лежать на одній прямій. Сполучивши крайні точки відрізком, одержимо графік залежності об'єму води в басейні від часу його наповнення.<br><br>Прочитайте<br><br>1. Користуючись графіком залежності об'єму води в басейні від часу його наповнення (рис. 80), знайти: а) об'єм, якщо 1= 13; б) час, якщо V=6. • а) На осі абсцис, на якій відкладали час І, позначаємо точку з абсцисою 13, проводимо через неї пряму, перпендикулярну до осі абсцис, та знаходимо точку перетину прямої з графіком. Через одержану на графіку точку проводимо<br> <br>пряму, перпендикулярну до осі ординат, на якій відкладали об'єм. Ордината точки перетину цієї прямої з віссю ординат дорівнює значенню об'єму: V= 6,5.<br>б) На осі ординат, на якій відкладали об'єм V, позначаємо точку з ординатою 6, будуємо перпендикулярну пряму та знаходимо точку її перетину з графіком. Через одержану на графіку точку проводимо пряму, перпендикулярну до осі абсцис, на якій відкладали час. Абсциса точки перетину цієї прямої та осі абсцис дорівнює значенню часу: 1= 12. •<br><br>Усно<br>1354. Автомобіль рухається зі швидкістю 80 км/год. Який шлях проїде автомобіль за 0,5 год; 1 год; 2 год; 2,5 год? За якою формулою можна обчислити шлях 5 (у км), пройдений автомобілем за час і (у год)?<br>1355. Площа прямокутника дорівнює 18 см2. Чому дорівнює сторона прямокутника, якщо інша його сторона дорівнює 3 см; 6 см; 36 см? За якою формулою можна обчислити сторону b (у см) прямокутника, знаючи довжину а (у см) іншої його сторони?<br> |
| | | | |
| - | Рівень А | + | Рівень А |
| | | | |
| - | [[Image:asd349.jpg]] | + | [[Image:Asd349.jpg]] |
| | | | |
| - | Один кілограм яблук коштує 3 грн. а) Запишіть формулу для обчислення вартості Р (у гривнях) к кілограмів яблук; б) користуючись формулою, заповніть таблицю: | + | Один кілограм яблук коштує 3 грн. а) Запишіть формулу для обчислення вартості Р (у гривнях) к кілограмів яблук; б) користуючись формулою, заповніть таблицю: |
| | | | |
| - | [[Image:asd350.jpg]] | + | [[Image:Asd350.jpg]] |
| | | | |
| - | в) побудуйте графік залежності вартості Р від маси к. 1358. Користуючись графіком залежності температури повітря від часу (рис. 81), знайдіть: а) температуру Т, якщо і = 4,5 год; ґ = 10 год; б) о котрій годині температура Т дорівнювала -3°С; 5°С.<br> Рівень Б<br><br>1360. Один метр тканини коштує 4 грн. Побудуйте графік залежності вартості тканини Р (у гривнях) від її довжини т (у метрах).<br> <br><br>1361. Один кілограм слив коштує 1,5 грн. Побудуйте графік залежності вартості слив Р (у гривнях) від їх маси к (у кілограмах).<br> <br>1362. Сувій тканини завдовжки 12 м коштує 36 грн. Побудуйте графік залежності вартості Р (у гривнях) сувою тканини від його довжини / (у метрах). Користуючись графіком, знайдіть вартість сувою тканини завдовжки 4,5 м.<br><br><br> Здогадайтеся<br><br>1363. Якщо Андрій половину уроків робить, переглядаючи телепередачі, а іншу половину — при вимкненому телевізорі, то затрачає 2 год. Якщо він усі уроки робить при вимкненому телевізорі, то затрачає 1 год. Скільки часу затратить Андрій на виконання домашніх завдань, коли робитиме їх при увімкненому телевізорі?<br>[[Image:asd351.jpg]] | + | в) побудуйте графік залежності вартості Р від маси к. 1358. Користуючись графіком залежності температури повітря від часу (рис. 81), знайдіть: а) температуру Т, якщо і = 4,5 год; ґ = 10 год; б) о котрій годині температура Т дорівнювала -3°С; 5°С.<br> Рівень Б<br><br>1360. Один метр тканини коштує 4 грн. Побудуйте графік залежності вартості тканини Р (у гривнях) від її довжини т (у метрах).<br> <br><br>1361. Один кілограм слив коштує 1,5 грн. Побудуйте графік залежності вартості слив Р (у гривнях) від їх маси к (у кілограмах).<br> <br>1362. Сувій тканини завдовжки 12 м коштує 36 грн. Побудуйте графік залежності вартості Р (у гривнях) сувою тканини від його довжини / (у метрах). Користуючись графіком, знайдіть вартість сувою тканини завдовжки 4,5 м.<br><br><br> Здогадайтеся<br><br>1363. Якщо Андрій половину уроків робить, переглядаючи телепередачі, а іншу половину — при вимкненому телевізорі, то затрачає 2 год. Якщо він усі уроки робить при вимкненому телевізорі, то затрачає 1 год. Скільки часу затратить Андрій на виконання домашніх завдань, коли робитиме їх при увімкненому телевізорі?<br>[[Image:Asd351.jpg]] |
| | | | |
| - | Памятка до §6<br>1. -5 • (-2) = |-5| • |—2| = 10 — перемножили модулі множників.<br> -5 • 2 = -10 — знаки множників різні, добуток — число від'ємне.<br>2. -20 : (-4) = |-20| : |-4| = 5 — поділили модуль діленого на модуль дільника. | + | Памятка до §6<br>1. -5 • (-2) = |-5| • |—2| = 10 — перемножили модулі множників.<br> -5 • 2 = -10 — знаки множників різні, добуток — число від'ємне.<br>2. -20 : (-4) = |-20| : |-4| = 5 — поділили модуль діленого на модуль дільника. |
| | | | |
| - | -20 : 4 = -5 — знаки діленого та дільника різні, частка — число від'ємне.<br>3. -7х ; -7 — коефіцієнт.<br>4. 7х + 12х; 7х і 12х — подібні доданки.<br>5. 7х + 12х = (7 + 12)х = 19х — звели подібні доданки, додали коефіцієнти, помножили на спільну буквену частину.<br><br>6 12х - 3 = 5х + 2; 12х - 5х = 2 + 3 — доданки можна переносити з однієї частини рівняння в іншу, змінюючи при цьому їх знаки на протилежні.<br>[[Image:seveen.jpg]] | + | -20 : 4 = -5 — знаки діленого та дільника різні, частка — число від'ємне.<br>3. -7х ; -7 — коефіцієнт.<br>4. 7х + 12х; 7х і 12х — подібні доданки.<br>5. 7х + 12х = (7 + 12)х = 19х — звели подібні доданки, додали коефіцієнти, помножили на спільну буквену частину.<br><br>6 12х - 3 = 5х + 2; 12х - 5х = 2 + 3 — доданки можна переносити з однієї частини рівняння в іншу, змінюючи при цьому їх знаки на протилежні.<br>[[Image:Seveen.jpg]] |
| | | | |
| - | [[Image:seveen1.jpg]] | + | [[Image:Seveen1.jpg]] |
| | | | |
| - | Запитання для самоперевірки і повторення<br>1. Як знайти добуток двох чисел із різними знаками?<br>2. Як знайти добуток двох від'ємних чисел?<br>3. Які властивості має множення раціональних чисел?<br>4. Що таке коефіцієнт виразу?<br>5. Які доданки називають подібними?<br>6. Як звести подібні доданки?<br>7. Як поділити два від'ємні числа?<br>8. Як поділити два числа з різними знаками?<br>9. Сформулюйте правило перенесення доданків з однієї частини рівняння в іншу.<br>10. Які прямі називають паралельними?<br>11. Які прямі називають перпендикулярними?<br>12. Що таке координатна площина?<br>Завдання для повторення §6<br>Виконайте дії:<br>1366. а) (-5 + 4,8)-(-0,5)2; б) (8 - 10,2) • (-9 + 7,5);<br>в) (-7-8 + 16,1)2; г) (-2,75 + 3) • (-0,2)2;<br>д) -18 : (-3 + 2,7) + 9; е) (-2)3:4 + (-0,8): (-0,04).<br>[[Image:asd352.jpg]] | + | Запитання для самоперевірки і повторення<br>1. Як знайти добуток двох чисел із різними знаками?<br>2. Як знайти добуток двох від'ємних чисел?<br>3. Які властивості має множення раціональних чисел?<br>4. Що таке коефіцієнт виразу?<br>5. Які доданки називають подібними?<br>6. Як звести подібні доданки?<br>7. Як поділити два від'ємні числа?<br>8. Як поділити два числа з різними знаками?<br>9. Сформулюйте правило перенесення доданків з однієї частини рівняння в іншу.<br>10. Які прямі називають паралельними?<br>11. Які прямі називають перпендикулярними?<br>12. Що таке координатна площина?<br>Завдання для повторення §6<br>Виконайте дії:<br>1366. а) (-5 + 4,8)-(-0,5)2; б) (8 - 10,2) • (-9 + 7,5);<br>в) (-7-8 + 16,1)2; г) (-2,75 + 3) • (-0,2)2;<br>д) -18 : (-3 + 2,7) + 9; е) (-2)3:4 + (-0,8): (-0,04).<br>[[Image:Asd352.jpg]] |
| | | | |
| - | 1372. Знайдіть різницю числа 9 і суми чисел -1,9 і-2,1.<br>1373. Від добутку чисел 3,25 і -4 відніміть число -1/3.<br>1374. До частки чисел -7,5 і -3 додайте добуток чисел -0,3 і 30.<br>1375. До добутку чисел -1,8 і 2 додайте частку чисел 24 і -1,2.<br>1376. На скільки сума чисел -1,64 і -0,36 більша від числа -10?<br>1377. На скільки сума чисел -13 і 4 більша від їх добутку?<br>Розв 'яжіть рівняння:<br>1378. а)х-2,3=-4,2; б)2х + 3,6 = 5;<br>[[Image:zapasss.jpg]] | + | 1372. Знайдіть різницю числа 9 і суми чисел -1,9 і-2,1.<br>1373. Від добутку чисел 3,25 і -4 відніміть число -1/3.<br>1374. До частки чисел -7,5 і -3 додайте добуток чисел -0,3 і 30.<br>1375. До добутку чисел -1,8 і 2 додайте частку чисел 24 і -1,2.<br>1376. На скільки сума чисел -1,64 і -0,36 більша від числа -10?<br>1377. На скільки сума чисел -13 і 4 більша від їх добутку?<br>Розв 'яжіть рівняння:<br>1378. а)х-2,3=-4,2; б)2х + 3,6 = 5;<br>[[Image:Zapasss.jpg]] |
| | | | |
| - | 1379. а)|х|-9 = 15; б)3|х| = 10; в)|х + 3| = 10.<br>1380. За якого значення а значення виразів -За + 11 і 1а- 1 рівні?<br>1381. Позначте на координатній площині точки А(-2; -2), /5(4; -2) і С(-2; 3).<br>а) Через точку С проведіть пряму, паралельну прямій АВ. Знайдіть коор-<br>динати двох точок, що належать проведеній прямій.<br>б) Через точку В проведіть пряму, перпендикулярну до прямої АС. Запишіть<br>координати двох точок, що належать проведеній прямій.<br>1382. Позначте на координатній площині точки А(-2; 3), /5(4; 3) і С(4;-1). Знайдіть координати точки Д яка є четвертою вершиною прямокутника АВСВ. Знайдіть периметр і площу цього прямокутника.<br>1383. Яке число задумали?<br>а) Якщо від задуманого числа відняти 42 й одержану різницю помножити<br>на 3, то одержимо 192.<br>б) Якщо задумане число помножити на 5 і до одержаного добутку додати<br>31, то отримаємо -104.<br>в) Якщо до потроєного задуманого числа додати подвоєне, то одержимо -90.<br>1384. На першій полиці книжок утричі більше, ніж на другій. Якщо з першої полиці перекласти 30 книжок на другу, то на обох полицях книжок стане порівну. Скільки книжок було на кожній полиці спочатку?<br>1385. У перший магазин відправили товару в 1,4 разу більше, ніж у другий. Коли до першого магазину відправили ще 120 кг товару, а до другого — 180 кг, то виявилось, що до обох магазинів відправили однакову кількість товару. Скільки товару відправили до кожного магазину спочатку?<br>1386. Одне число більше від іншого у 2,5 разу. Коли від більшого числа відняли 69, а до меншого додали 21, то одержали однакові результати. Чому дорівнюють ці числа?<br>1387. У трьох ящиках є 35 кг слив. У першому в 1,2 разу більше, ніж у другому, а в третьому на 3 кг більше, ніж у другому. Скільки слив у кожному ящику?<br>1388. Відстань від міста до села автобус долає за 2/3 год, а легковий автомобіль,<br>швидкість якого на 20 км/год більша, — за 1/2 год. Знайдіть швидкість автомобіля. Яка відстань від міста до села?<br> <br>Завдання для самоперевірки<br><br>/ рівень<br><br>1. Обчисліть: -11-7.<br>а) 77; б)-74; в)-77; г)-87.<br>2. Обчисліть: -12 • (-6).<br>а) 72; б)-72; в) 62; г)-62.<br>3. Обчисліть: -45 : (-15).<br>а)-3; 6)5; в) 2,5; г) 3.<br>4. Зведіть подібні доданки: 17а + 5а - 10а + 3.<br>а)12а + 3; 6)12 + 3; в) 15; г)2а + 3.<br>5. Розв'яжіть рівняння: 5х - 3 = 2х.<br>а)|; 6)1; в)-1; г) -|.<br><br>6. Які координати має точка 4?<br>[[Image:asd353.jpg]] | + | 1379. а)|х|-9 = 15; б)3|х| = 10; в)|х + 3| = 10.<br>1380. За якого значення а значення виразів -За + 11 і 1а- 1 рівні?<br>1381. Позначте на координатній площині точки А(-2; -2), /5(4; -2) і С(-2; 3).<br>а) Через точку С проведіть пряму, паралельну прямій АВ. Знайдіть коор-<br>динати двох точок, що належать проведеній прямій.<br>б) Через точку В проведіть пряму, перпендикулярну до прямої АС. Запишіть<br>координати двох точок, що належать проведеній прямій.<br>1382. Позначте на координатній площині точки А(-2; 3), /5(4; 3) і С(4;-1). Знайдіть координати точки Д яка є четвертою вершиною прямокутника АВСВ. Знайдіть периметр і площу цього прямокутника.<br>1383. Яке число задумали?<br>а) Якщо від задуманого числа відняти 42 й одержану різницю помножити<br>на 3, то одержимо 192.<br>б) Якщо задумане число помножити на 5 і до одержаного добутку додати<br>31, то отримаємо -104.<br>в) Якщо до потроєного задуманого числа додати подвоєне, то одержимо -90.<br>1384. На першій полиці книжок утричі більше, ніж на другій. Якщо з першої полиці перекласти 30 книжок на другу, то на обох полицях книжок стане порівну. Скільки книжок було на кожній полиці спочатку?<br>1385. У перший магазин відправили товару в 1,4 разу більше, ніж у другий. Коли до першого магазину відправили ще 120 кг товару, а до другого — 180 кг, то виявилось, що до обох магазинів відправили однакову кількість товару. Скільки товару відправили до кожного магазину спочатку?<br>1386. Одне число більше від іншого у 2,5 разу. Коли від більшого числа відняли 69, а до меншого додали 21, то одержали однакові результати. Чому дорівнюють ці числа?<br>1387. У трьох ящиках є 35 кг слив. У першому в 1,2 разу більше, ніж у другому, а в третьому на 3 кг більше, ніж у другому. Скільки слив у кожному ящику?<br>1388. Відстань від міста до села автобус долає за 2/3 год, а легковий автомобіль,<br>швидкість якого на 20 км/год більша, — за 1/2 год. Знайдіть швидкість автомобіля. Яка відстань від міста до села?<br> <br>Завдання для самоперевірки<br><br>/ рівень<br><br>1. Обчисліть: -11-7.<br>а) 77; б)-74; в)-77; г)-87.<br>2. Обчисліть: -12 • (-6).<br>а) 72; б)-72; в) 62; г)-62.<br>3. Обчисліть: -45 : (-15).<br>а)-3; 6)5; в) 2,5; г) 3.<br>4. Зведіть подібні доданки: 17а + 5а - 10а + 3.<br>а)12а + 3; 6)12 + 3; в) 15; г)2а + 3.<br>5. Розв'яжіть рівняння: 5х - 3 = 2х.<br>а)|; 6)1; в)-1; г) -|.<br><br>6. Які координати має точка 4?<br>[[Image:Asd353.jpg]] |
| | | | |
| - | а)(1;2); б)(-1;-2); в)(2;-1); г)(-1;2).<br><br>// рівень<br><br>7. Обчисліть:<br>а)-2,8-15; б)-5-(-1,6); в) 9: (-1,5).<br>8. Спростіть вираз:<br>а) -(а + 2) + 2(4 - За); 6) -4(-2,5 - 2х) + 2(-1,8х + 1).<br>9. Розв'яжіть рівняння:<br>а) 2х - 3 = 5 -Зх; b) 4(-3,5 + Зх) = -3 + 10x. | + | а)(1;2); б)(-1;-2); в)(2;-1); г)(-1;2).<br><br>// рівень<br><br>7. Обчисліть:<br>а)-2,8-15; б)-5-(-1,6); в) 9: (-1,5).<br>8. Спростіть вираз:<br>а) -(а + 2) + 2(4 - За); 6) -4(-2,5 - 2х) + 2(-1,8х + 1).<br>9. Розв'яжіть рівняння:<br>а) 2х - 3 = 5 -Зх; b) 4(-3,5 + Зх) = -3 + 10x. |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:Asd354.jpg]]<br>12. У трьох бідонах є 92 л молока, до того ж, у другому бідоні молока удвічі більше, а у третьому — на 4 л менше, ніж у першому. Скільки молока в кожному бідоні? |
| | | | |
| - | [[Image:asd354.jpg]]<br>12. У трьох бідонах є 92 л молока, до того ж, у другому бідоні молока удвічі більше, а у третьому — на 4 л менше, ніж у першому. Скільки молока в кожному бідоні?
| + | <br>IV рівень<br>13. Знайдіть значення виразу (2а - 8/3 + 3) • (-2) - 5(-а + 1,8/3 - 1,4), якщо а = -5; /3=1.<br>14. Шлях між двома містами автомобіль подолав за 1,5 год, а мотоцикліст — за 2 год. Знайдіть відстань між містами, якщо швидкість мотоцикліста на 18 км/год менша від швидкості автомобіля.<br>15. У першому сховищі є 120 кг яблук, а в другому — 90 кг яблук. Щогодини з першого сховища беруть по 15 кг яблук, а з другого — по 5 кг яблук. Через скільки годин у першому сховищі залишиться яблук удвічі менше, ніж у другому?<br> |
| | | | |
| - | <br>IV рівень<br>13. Знайдіть значення виразу (2а - 8/3 + 3) • (-2) - 5(-а + 1,8/3 - 1,4), якщо а = -5; /3=1.<br>14. Шлях між двома містами автомобіль подолав за 1,5 год, а мотоцикліст — за 2 год. Знайдіть відстань між містами, якщо швидкість мотоцикліста на 18 км/год менша від швидкості автомобіля.<br>15. У першому сховищі є 120 кг яблук, а в другому — 90 кг яблук. Щогодини з першого сховища беруть по 15 кг яблук, а з другого — по 5 кг яблук. Через скільки годин у першому сховищі залишиться яблук удвічі менше, ніж у другому?<br><br> Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту | + | <br> <sub>[[Гіпермаркет Знань - перший в світі!|Онлайн-бібліотека з підручниками]] і книгами, тести [[Математика|з математики]], завдання [[Математика 6 клас|з математики 6 клас]], календарне планування</sub><br> Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту |
| | | | |
| | [[Image:1236084776 kr.jpg|10x10px]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B2%D0%B8%D1%87%D0%B0%D0%B9%D0%BD%D0%B8%D1%85_%D0%B4%D1%80%D0%BE%D0%B1%D1%96%D0%B2._%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D1%83_%D1%96_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%B8%D0%B9_%D0%BA%D0%B0%D1%80%D0%BA%D0%B0%D1%81 конспект уроку і опорний каркас] | | [[Image:1236084776 kr.jpg|10x10px]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B2%D0%B8%D1%87%D0%B0%D0%B9%D0%BD%D0%B8%D1%85_%D0%B4%D1%80%D0%BE%D0%B1%D1%96%D0%B2._%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D1%83_%D1%96_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%B8%D0%B9_%D0%BA%D0%B0%D1%80%D0%BA%D0%B0%D1%81 конспект уроку і опорний каркас] |
| Строка 85: |
Строка 87: |
| | | | |
| | | | |
| - | | + | <br> |
| | | | |
| | Если у вас есть исправления или предложения к данному уроку, напишите нам. | | Если у вас есть исправления или предложения к данному уроку, напишите нам. |
| | | | |
| | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. | | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Версия 09:20, 16 марта 2010
Гіпермаркет Знань>>Математика>>Математика 6 клас>> Математика: Тема 5.МНОЖЕННЯ І ДІЛЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ . Приклади графіків залежностей між величинами .
Метеорологи вимірювали температуру повітря протягом першої половини доби і результати записали до таблиці:

Потім вони вирішили нанести результати вимірювання на координатну площину, відклавши на осі абсцис значення часу (7, год), а на осі ординат — значення температури (Т, °С). Було позначено 13 точок: (0; -2), (1; -3,5), (12; 6). Абсциса кожної з цих точок — це значення часу, а ордината — значення температури повітря у цей час. Якби метеорологи вимірювали температуру щопівгодини і результати вимірювання наносили на координатну площину, то точки знаходилися б ближче одна до одної. Якби вимірювання проводилося щочверть години, то точки на координатній площині були б розміщені ще густіше і т. д.
Якщо точки, побудовані таким чином на координатній площині, сполучити плавною лінією, то одержимо фігуру, яку називають графіком залежності температури повітря від часу (рис. 78).
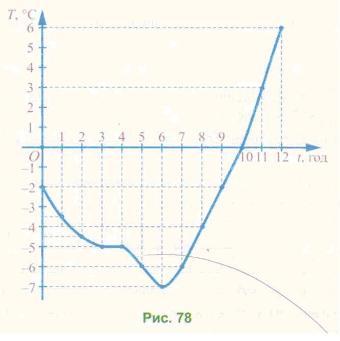
Розглянемо ще такі приклади.
1. Туристові потрібно пройти 12 км. Він вирахував час руху залежно від швидкості, з якою йтиме, й одержав таку таблицю:

Побудуємо на координатній площині точки за цією таблицею, відклавши на осі абсцис значення швидкості (v, км/год), а на осі ординат — значення часу (і, год).
Сполучивши плавною лінією побудовані точки, одержимо графік залежності часу від швидкості за сталої відстані (12 км) (рис. 79).
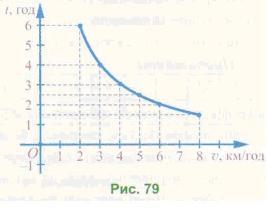
Цю залежність часу t (у год) від швидкості u (у км/год), можна задати 12
формулою t = 12/u .
2, Відомо, що до басейну щосекунди вливається 0,5 м3 води. Потрібно знайти, скільки буде води в басейні через t с.
Залежність об'єму води У(у м3) від часу / (у секундах) можна задати формулою V= 0,5?.
Надамо / певних значень, знайдемо відповідні значення об'єму води в басейні і результати занесемо до таблиці:

За даними таблиці побудуємо на координатній площині точки, відклавши на осі абсцис значення часу (і, с), а на осі ординат — значення об'єму (V, м3).
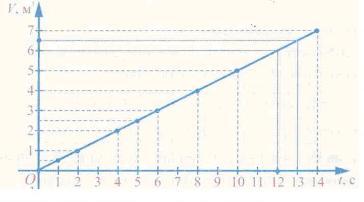
Рис. 80
Приклавши лінійку до побудованих точок, бачимо, що вони лежать на одній прямій. Сполучивши крайні точки відрізком, одержимо графік залежності об'єму води в басейні від часу його наповнення.
Прочитайте
1. Користуючись графіком залежності об'єму води в басейні від часу його наповнення (рис. 80), знайти: а) об'єм, якщо 1= 13; б) час, якщо V=6. • а) На осі абсцис, на якій відкладали час І, позначаємо точку з абсцисою 13, проводимо через неї пряму, перпендикулярну до осі абсцис, та знаходимо точку перетину прямої з графіком. Через одержану на графіку точку проводимо
пряму, перпендикулярну до осі ординат, на якій відкладали об'єм. Ордината точки перетину цієї прямої з віссю ординат дорівнює значенню об'єму: V= 6,5.
б) На осі ординат, на якій відкладали об'єм V, позначаємо точку з ординатою 6, будуємо перпендикулярну пряму та знаходимо точку її перетину з графіком. Через одержану на графіку точку проводимо пряму, перпендикулярну до осі абсцис, на якій відкладали час. Абсциса точки перетину цієї прямої та осі абсцис дорівнює значенню часу: 1= 12. •
Усно
1354. Автомобіль рухається зі швидкістю 80 км/год. Який шлях проїде автомобіль за 0,5 год; 1 год; 2 год; 2,5 год? За якою формулою можна обчислити шлях 5 (у км), пройдений автомобілем за час і (у год)?
1355. Площа прямокутника дорівнює 18 см2. Чому дорівнює сторона прямокутника, якщо інша його сторона дорівнює 3 см; 6 см; 36 см? За якою формулою можна обчислити сторону b (у см) прямокутника, знаючи довжину а (у см) іншої його сторони?
Рівень А

Один кілограм яблук коштує 3 грн. а) Запишіть формулу для обчислення вартості Р (у гривнях) к кілограмів яблук; б) користуючись формулою, заповніть таблицю:

в) побудуйте графік залежності вартості Р від маси к. 1358. Користуючись графіком залежності температури повітря від часу (рис. 81), знайдіть: а) температуру Т, якщо і = 4,5 год; ґ = 10 год; б) о котрій годині температура Т дорівнювала -3°С; 5°С.
Рівень Б
1360. Один метр тканини коштує 4 грн. Побудуйте графік залежності вартості тканини Р (у гривнях) від її довжини т (у метрах).
1361. Один кілограм слив коштує 1,5 грн. Побудуйте графік залежності вартості слив Р (у гривнях) від їх маси к (у кілограмах).
1362. Сувій тканини завдовжки 12 м коштує 36 грн. Побудуйте графік залежності вартості Р (у гривнях) сувою тканини від його довжини / (у метрах). Користуючись графіком, знайдіть вартість сувою тканини завдовжки 4,5 м.
Здогадайтеся
1363. Якщо Андрій половину уроків робить, переглядаючи телепередачі, а іншу половину — при вимкненому телевізорі, то затрачає 2 год. Якщо він усі уроки робить при вимкненому телевізорі, то затрачає 1 год. Скільки часу затратить Андрій на виконання домашніх завдань, коли робитиме їх при увімкненому телевізорі?

Памятка до §6
1. -5 • (-2) = |-5| • |—2| = 10 — перемножили модулі множників.
-5 • 2 = -10 — знаки множників різні, добуток — число від'ємне.
2. -20 : (-4) = |-20| : |-4| = 5 — поділили модуль діленого на модуль дільника.
-20 : 4 = -5 — знаки діленого та дільника різні, частка — число від'ємне.
3. -7х ; -7 — коефіцієнт.
4. 7х + 12х; 7х і 12х — подібні доданки.
5. 7х + 12х = (7 + 12)х = 19х — звели подібні доданки, додали коефіцієнти, помножили на спільну буквену частину.
6 12х - 3 = 5х + 2; 12х - 5х = 2 + 3 — доданки можна переносити з однієї частини рівняння в іншу, змінюючи при цьому їх знаки на протилежні.


Запитання для самоперевірки і повторення
1. Як знайти добуток двох чисел із різними знаками?
2. Як знайти добуток двох від'ємних чисел?
3. Які властивості має множення раціональних чисел?
4. Що таке коефіцієнт виразу?
5. Які доданки називають подібними?
6. Як звести подібні доданки?
7. Як поділити два від'ємні числа?
8. Як поділити два числа з різними знаками?
9. Сформулюйте правило перенесення доданків з однієї частини рівняння в іншу.
10. Які прямі називають паралельними?
11. Які прямі називають перпендикулярними?
12. Що таке координатна площина?
Завдання для повторення §6
Виконайте дії:
1366. а) (-5 + 4,8)-(-0,5)2; б) (8 - 10,2) • (-9 + 7,5);
в) (-7-8 + 16,1)2; г) (-2,75 + 3) • (-0,2)2;
д) -18 : (-3 + 2,7) + 9; е) (-2)3:4 + (-0,8): (-0,04).

1372. Знайдіть різницю числа 9 і суми чисел -1,9 і-2,1.
1373. Від добутку чисел 3,25 і -4 відніміть число -1/3.
1374. До частки чисел -7,5 і -3 додайте добуток чисел -0,3 і 30.
1375. До добутку чисел -1,8 і 2 додайте частку чисел 24 і -1,2.
1376. На скільки сума чисел -1,64 і -0,36 більша від числа -10?
1377. На скільки сума чисел -13 і 4 більша від їх добутку?
Розв 'яжіть рівняння:
1378. а)х-2,3=-4,2; б)2х + 3,6 = 5;
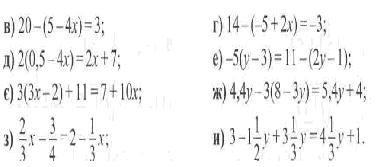
1379. а)|х|-9 = 15; б)3|х| = 10; в)|х + 3| = 10.
1380. За якого значення а значення виразів -За + 11 і 1а- 1 рівні?
1381. Позначте на координатній площині точки А(-2; -2), /5(4; -2) і С(-2; 3).
а) Через точку С проведіть пряму, паралельну прямій АВ. Знайдіть коор-
динати двох точок, що належать проведеній прямій.
б) Через точку В проведіть пряму, перпендикулярну до прямої АС. Запишіть
координати двох точок, що належать проведеній прямій.
1382. Позначте на координатній площині точки А(-2; 3), /5(4; 3) і С(4;-1). Знайдіть координати точки Д яка є четвертою вершиною прямокутника АВСВ. Знайдіть периметр і площу цього прямокутника.
1383. Яке число задумали?
а) Якщо від задуманого числа відняти 42 й одержану різницю помножити
на 3, то одержимо 192.
б) Якщо задумане число помножити на 5 і до одержаного добутку додати
31, то отримаємо -104.
в) Якщо до потроєного задуманого числа додати подвоєне, то одержимо -90.
1384. На першій полиці книжок утричі більше, ніж на другій. Якщо з першої полиці перекласти 30 книжок на другу, то на обох полицях книжок стане порівну. Скільки книжок було на кожній полиці спочатку?
1385. У перший магазин відправили товару в 1,4 разу більше, ніж у другий. Коли до першого магазину відправили ще 120 кг товару, а до другого — 180 кг, то виявилось, що до обох магазинів відправили однакову кількість товару. Скільки товару відправили до кожного магазину спочатку?
1386. Одне число більше від іншого у 2,5 разу. Коли від більшого числа відняли 69, а до меншого додали 21, то одержали однакові результати. Чому дорівнюють ці числа?
1387. У трьох ящиках є 35 кг слив. У першому в 1,2 разу більше, ніж у другому, а в третьому на 3 кг більше, ніж у другому. Скільки слив у кожному ящику?
1388. Відстань від міста до села автобус долає за 2/3 год, а легковий автомобіль,
швидкість якого на 20 км/год більша, — за 1/2 год. Знайдіть швидкість автомобіля. Яка відстань від міста до села?
Завдання для самоперевірки
/ рівень
1. Обчисліть: -11-7.
а) 77; б)-74; в)-77; г)-87.
2. Обчисліть: -12 • (-6).
а) 72; б)-72; в) 62; г)-62.
3. Обчисліть: -45 : (-15).
а)-3; 6)5; в) 2,5; г) 3.
4. Зведіть подібні доданки: 17а + 5а - 10а + 3.
а)12а + 3; 6)12 + 3; в) 15; г)2а + 3.
5. Розв'яжіть рівняння: 5х - 3 = 2х.
а)|; 6)1; в)-1; г) -|.
6. Які координати має точка 4?
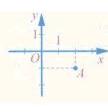
а)(1;2); б)(-1;-2); в)(2;-1); г)(-1;2).
// рівень
7. Обчисліть:
а)-2,8-15; б)-5-(-1,6); в) 9: (-1,5).
8. Спростіть вираз:
а) -(а + 2) + 2(4 - За); 6) -4(-2,5 - 2х) + 2(-1,8х + 1).
9. Розв'яжіть рівняння:
а) 2х - 3 = 5 -Зх; b) 4(-3,5 + Зх) = -3 + 10x.

12. У трьох бідонах є 92 л молока, до того ж, у другому бідоні молока удвічі більше, а у третьому — на 4 л менше, ніж у першому. Скільки молока в кожному бідоні?
IV рівень
13. Знайдіть значення виразу (2а - 8/3 + 3) • (-2) - 5(-а + 1,8/3 - 1,4), якщо а = -5; /3=1.
14. Шлях між двома містами автомобіль подолав за 1,5 год, а мотоцикліст — за 2 год. Знайдіть відстань між містами, якщо швидкість мотоцикліста на 18 км/год менша від швидкості автомобіля.
15. У першому сховищі є 120 кг яблук, а в другому — 90 кг яблук. Щогодини з першого сховища беруть по 15 кг яблук, а з другого — по 5 кг яблук. Через скільки годин у першому сховищі залишиться яблук удвічі менше, ніж у другому?
Онлайн-бібліотека з підручниками і книгами, тести з математики, завдання з математики 6 клас, календарне планування
Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту
 конспект уроку і опорний каркас конспект уроку і опорний каркас
 презентація уроку презентація уроку
 акселеративні методи та інтерактивні технології акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями) закриті вправи (тільки для використання вчителями)
 оцінювання
Практика оцінювання
Практика
 задачі та вправи,самоперевірка задачі та вправи,самоперевірка
 практикуми, лабораторні, кейси практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання
Ілюстрації домашнє завдання
Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати реферати
 фішки для допитливих фішки для допитливих
 шпаргалки шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення
 зовнішнє незалежне тестування (ЗНТ) зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні підручники основні і допоміжні
 тематичні свята, девізи тематичні свята, девізи
 статті статті
 національні особливості національні особливості
 словник термінів словник термінів
 інше
Тільки для вчителів інше
Тільки для вчителів
 ідеальні уроки ідеальні уроки
 календарний план на рік календарний план на рік
 методичні рекомендації методичні рекомендації
 програми програми
 обговорення обговорення
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|