|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Газовые законы</metakeywords> | | <metakeywords>Физика, 10 класс, Газовые законы</metakeywords> |
| | | | |
| - | С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трех параметров - давление, объем или температура - остаются неизменными. Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют ''газовыми законами''.<br> Процессы, протекающие при неизменном значении одного из параметров, называют ''изопроцессами'' (от греческого слова «изос» - равный). Правда, в действительности ни один процесс не может протекать при строго фиксированном значении какого-либо параметра. Всегда имеются те или иные воздействия, нарушающие постоянство температуры, давления или объема. Лишь в лабораторных условиях удается поддерживать постоянство того или иного параметра с высокой точностью, но в действующих технических устройствах и в природе это практически неосуществимо. Изопроцесс - это идеализированная модель реального процесса, которая только приближенно отражает действительность.<br> '''Изотермический процесс.''' Процесс изменения состояния системы макроскопических тел (''термодинамической системы'') при постоянной температуре называют '''изотермическим'''. Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой - термостатом. Иначе при сжатии или расширении температура газа будет меняться. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.<br> Согласно уравнению состояния идеального газа (10.4) в любом состоянии с неизменной температурой произведение давления газа на его объем остается постоянным:<br>[[Image:a69-1.jpg|center]] '''''Для газа данной массы при постоянной температуре произведение давления газа на его объем постоянно.'''''<br> Этот закон экспериментально был открыт английским ученым Р. Бойлем (1627-1691) и несколько позже французским ученым Э. Мариоттом (1620-1684). Поэтому он носит название'''''закона Бойля - Мариотта'''''.<br> Закон Бойля - Мариотта справедлив обычно для любых газов, а также и для их смесей, например для воздуха.<br>Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.<br> Зависимость давления газа от объема при постоянной температуре графически изображают кривой, которую называют '''изотермой'''. Изотерма газа изображает обратно пропорциональную зависимость между давлением и объемом. Кривую такого рода в математике называют гиперболой (''рис.10.1'').<br>[[Image:a10.1.jpg|center]] Различным постоянным температурам соответствуют различные изотермы. При повышении температуры газа давление согласно уравнению состояния (10.4) увеличивается, если ''V''=const. Поэтому изотерма, соответствующая более высокой температуре ''T<sub>2</sub>'', лежит выше изотермы, соответствующей более низкой температуре ''T<sub>1</sub>'' (см. ''рис.10.1'').<br> Для того чтобы процесс происходил при постоянной температуре, сжатие или расширение газа должно происходить очень медленно. Дело в том, что, например, при сжатии газ нагревается, так как при движении поршня в сосуде скорость молекул после ударов о поршень увеличивается, а следовательно, увеличивается и температура газа. Именно поэтому для реализации изотермического процесса надо после небольшого смещения поршня подождать, когда температура газа в сосуде опять станет равной температуре окружающего воздуха.<br> Кроме этого, отметим, что при быстром сжатии давление под поршнем сразу становится больше, чем во всем сосуде. Если значения давления и температуры в различных точках объема разные, то в этом случае газ находится в неравновесном состоянии и мы не можем назвать значения температуры и давления, определяющие в данный момент состояние системы. Если систему предоставить самой себе, то температура и давление постепенно выравниваются, система приходит в равновесное состояние. ''Равновесное состояние'' - это состояние, при котором температура и давление во всех точках объема одинаковы. Параметры состояния газа могут быть определены, если он находится в равновесном состоянии. Процесс, при котором все промежуточные состояния газа являются равновесными, называют ''равновесным процессом''. Очевидно, что на графиках зависимости одного параметра от другого мы можем изображать только равновесные процессы.<br> '''Изобарный процесс.''' Процесс изменения состояния термодинамической системы при постоянном давлении называют '''изобарным''' (от греческого слова «барос» - вес).<br> Согласно уравнению (10.4) в любом состоянии газа с неизменным давлением отношение объема газа к его температуре остается постоянным: <br>[[Image:a69-2.jpg|center]] '''''Для газа данной массы при постоянном давлении отношение объема к температуре постоянно.'''''<br> Этот закон был установлен экспериментально в 1802 г. французским ученым Ж. Гей-Люссаком (1778-1850) и носит название '''''закона Гей-Люссака'''''. Согласно уравнению (10.7) объем газа при постоянном давлении пропорционален температуре:<br>[[Image:a69-3.jpg|center]] Эта зависимость графически изображается прямой, которая называется ''изобарой'' (''рис.10.2''). Разным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре согласно закону Бойля - Мариотта уменьшается. Поэтому изобара, соответствующая более высокому давлению ''p<sub>2</sub>'', лежит ниже изобары, соответствующей более низкому давлению ''p<sub>1</sub>''.<br>[[Image:a10.2.jpg|center]] В области низких температур все изобары ''идеального'' газа сходятся в точке ''T''=0. Но это не означает, что объем ''реального'' газа обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния (10.4) неприменимо. Именно поэтому, начиная с некоторого значения температуры, зависимость объема от температуры проводится на графике штриховой линией. В действительности таких значений температуры и давления у вещества в газообразном состоянии быть не может.<br> Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем, если внешнее давление постоянно. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня.<br> '''Изохорный процесс.''' Процесс изменения состояния термодинамической системы при постоянном объеме называют '''изохорным''' (от греческого слова «хорема» - вместимость).<br> Из уравнения состояния (10.4) вытекает, что в любом состоянии газа с неизменным объемом отношение давления газа к его температуре остается постоянным: <br>[[Image:a69-4.jpg|center]] '''''Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.'''''<br> Этот газовый закон был установлен в 1787 г. французским физиком Ж.Шарлем (1746-1823) и носит название '''''закона Шарля'''''. Согласно уравнению (10.9) давление газа при постоянном объеме пропорционально температуре:<br>[[Image:a69-5.jpg|center]] Эта зависимость изображается прямой, называемой ''изохорой'' (''рис.10.3''). Разным объемам соответствуют разные изохоры. С ростом объема газа при постоянной температуре давление его согласно закону Бойля - Мариотта падает. Поэтому изохора, соответствующая большему объему ''V<sub>2</sub>'', лежит ниже изохоры, соответствующей меньшему объему ''V<sub>1</sub>''.<br>[[Image:a10.3.jpg|center]] В соответствии с уравнением (10.10) все изохоры идеального газа начинаются в точке ''T''=0. Значит, давление идеального газа при абсолютном нуле равно нулю.<br> Увеличение давления газа в любом сосуде или в электрической лампочке при нагревании можно считать изохорным процессом. Изохорный процесс используется в газовых термометрах постоянного объема.<br> Газовые законы - частный случай уравнения состояния идеального газа, один из параметров которого остается постоянным.<br><br><br> ???<br> 1. Вы надули щеки. При этом и объем и давление воздуха у вас во рту увеличиваются. Как это согласовать с законом Бойля – Мариотта?<br> 2. Как можно осуществить изотермический, изобарный и изохорный процессы?<br> 3. Какое состояние системы (газа) считается равновесным?<br> 4. Как качественно объяснить газовые законы на основе молекулярно-кинетической теории?<br>
| + | С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трех параметров - давление, объем или температура - остаются неизменными. Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют ''газовыми законами''.<br> Процессы, протекающие при неизменном значении одного из параметров, называют ''изопроцессами'' (от греческого слова «изос» - равный). Правда, в действительности ни один процесс не может протекать при строго фиксированном значении какого-либо параметра. Всегда имеются те или иные воздействия, нарушающие постоянство температуры, давления или объема. Лишь в лабораторных условиях удается поддерживать постоянство того или иного параметра с высокой точностью, но в действующих технических устройствах и в природе это практически неосуществимо. Изопроцесс - это идеализированная модель реального процесса, которая только приближенно отражает действительность.<br> '''Изотермический процесс.''' Процесс изменения состояния системы макроскопических тел (''термодинамической системы'') при постоянной температуре называют '''изотермическим'''. Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой - термостатом. Иначе при сжатии или расширении температура газа будет меняться. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.<br> Согласно уравнению состояния идеального газа (10.4) в любом состоянии с неизменной температурой произведение давления газа на его объем остается постоянным:<br>[[Image:A69-1.jpg|center|341x20px]] '''''Для газа данной массы при постоянной температуре произведение давления газа на его объем постоянно.'''''<br> Этот закон экспериментально был открыт английским ученым Р. Бойлем (1627-1691) и несколько позже французским ученым Э. Мариоттом (1620-1684). Поэтому он носит название'''''закона Бойля - Мариотта'''''.<br> Закон Бойля - Мариотта справедлив обычно для любых газов, а также и для их смесей, например для воздуха.<br>Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.<br> Зависимость давления газа от объема при постоянной температуре графически изображают кривой, которую называют '''изотермой'''. Изотерма газа изображает обратно пропорциональную зависимость между давлением и объемом. Кривую такого рода в математике называют гиперболой (''рис.10.1'').<br>[[Image:A10.1.jpg|center|198x190px]] Различным постоянным температурам соответствуют различные изотермы. При повышении температуры газа давление согласно уравнению состояния (10.4) увеличивается, если ''V''=const. Поэтому изотерма, соответствующая более высокой температуре ''T<sub>2</sub>'', лежит выше изотермы, соответствующей более низкой температуре ''T<sub>1</sub>'' (см. ''рис.10.1'').<br> Для того чтобы процесс происходил при постоянной температуре, сжатие или расширение газа должно происходить очень медленно. Дело в том, что, например, при сжатии газ нагревается, так как при движении поршня в сосуде скорость молекул после ударов о поршень увеличивается, а следовательно, увеличивается и температура газа. Именно поэтому для реализации изотермического процесса надо после небольшого смещения поршня подождать, когда температура газа в сосуде опять станет равной температуре окружающего воздуха.<br> Кроме этого, отметим, что при быстром сжатии давление под поршнем сразу становится больше, чем во всем сосуде. Если значения давления и температуры в различных точках объема разные, то в этом случае газ находится в неравновесном состоянии и мы не можем назвать значения температуры и давления, определяющие в данный момент состояние системы. Если систему предоставить самой себе, то температура и давление постепенно выравниваются, система приходит в равновесное состояние. ''Равновесное состояние'' - это состояние, при котором температура и давление во всех точках объема одинаковы. Параметры состояния газа могут быть определены, если он находится в равновесном состоянии. Процесс, при котором все промежуточные состояния газа являются равновесными, называют ''равновесным процессом''. Очевидно, что на графиках зависимости одного параметра от другого мы можем изображать только равновесные процессы.<br> '''Изобарный процесс.''' Процесс изменения состояния термодинамической системы при постоянном давлении называют '''изобарным''' (от греческого слова «барос» - вес).<br> Согласно уравнению (10.4) в любом состоянии газа с неизменным давлением отношение объема газа к его температуре остается постоянным: <br>[[Image:A69-2.jpg|center|262x30px]] '''''Для газа данной массы при постоянном давлении отношение объема к температуре постоянно.'''''<br> Этот закон был установлен экспериментально в 1802 г. французским ученым Ж. Гей-Люссаком (1778-1850) и носит название '''''закона Гей-Люссака'''''. Согласно уравнению (10.7) объем газа при постоянном давлении пропорционален температуре:<br>[[Image:A69-3.jpg|center|179x16px]] Эта зависимость графически изображается прямой, которая называется ''изобарой'' (''рис.10.2''). Разным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре согласно закону Бойля - Мариотта уменьшается. Поэтому изобара, соответствующая более высокому давлению ''p<sub>2</sub>'', лежит ниже изобары, соответствующей более низкому давлению ''p<sub>1</sub>''.<br>[[Image:A10.2.jpg|center|175x171px]] В области низких температур все изобары ''идеального'' газа сходятся в точке ''T''=0. Но это не означает, что объем ''реального'' газа обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния (10.4) неприменимо. Именно поэтому, начиная с некоторого значения температуры, зависимость объема от температуры проводится на графике штриховой линией. В действительности таких значений температуры и давления у вещества в газообразном состоянии быть не может.<br> Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем, если внешнее давление постоянно. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня.<br> '''Изохорный процесс.''' Процесс изменения состояния термодинамической системы при постоянном объеме называют '''изохорным''' (от греческого слова «хорема» - вместимость).<br> Из уравнения состояния (10.4) вытекает, что в любом состоянии газа с неизменным объемом отношение давления газа к его температуре остается постоянным: <br>[[Image:A69-4.jpg|center|290x31px]] '''''Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.'''''<br> Этот газовый закон был установлен в 1787 г. французским физиком Ж.Шарлем (1746-1823) и носит название '''''закона Шарля'''''. Согласно уравнению (10.9) давление газа при постоянном объеме пропорционально температуре:<br>[[Image:A69-5.jpg|center|207x18px]] Эта зависимость изображается прямой, называемой ''изохорой'' (''рис.10.3''). Разным объемам соответствуют разные изохоры. С ростом объема газа при постоянной температуре давление его согласно закону Бойля - Мариотта падает. Поэтому изохора, соответствующая большему объему ''V<sub>2</sub>'', лежит ниже изохоры, соответствующей меньшему объему ''V<sub>1</sub>''.<br>[[Image:A10.3.jpg|center|179x187px]] В соответствии с уравнением (10.10) все изохоры идеального газа начинаются в точке ''T''=0. Значит, давление идеального газа при абсолютном нуле равно нулю.<br> Увеличение давления газа в любом сосуде или в электрической лампочке при нагревании можно считать изохорным процессом. Изохорный процесс используется в газовых термометрах постоянного объема.<br> Газовые законы - частный случай уравнения состояния идеального газа, один из параметров которого остается постоянным.<br><br><br> ???<br> 1. Вы надули щеки. При этом и объем и давление воздуха у вас во рту увеличиваются. Как это согласовать с законом Бойля – Мариотта?<br> 2. Как можно осуществить изотермический, изобарный и изохорный процессы?<br> 3. Какое состояние системы (газа) считается равновесным?<br> 4. Как качественно объяснить газовые законы на основе молекулярно-кинетической теории?<br> |
| | | | |
| - | | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | |
| | | | |
| | <br> | | <br> |
Версия 14:28, 21 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Газовые законы
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трех параметров - давление, объем или температура - остаются неизменными. Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют газовыми законами.
Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами (от греческого слова «изос» - равный). Правда, в действительности ни один процесс не может протекать при строго фиксированном значении какого-либо параметра. Всегда имеются те или иные воздействия, нарушающие постоянство температуры, давления или объема. Лишь в лабораторных условиях удается поддерживать постоянство того или иного параметра с высокой точностью, но в действующих технических устройствах и в природе это практически неосуществимо. Изопроцесс - это идеализированная модель реального процесса, которая только приближенно отражает действительность.
Изотермический процесс. Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре называют изотермическим. Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой - термостатом. Иначе при сжатии или расширении температура газа будет меняться. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.
Согласно уравнению состояния идеального газа (10.4) в любом состоянии с неизменной температурой произведение давления газа на его объем остается постоянным:
Для газа данной массы при постоянной температуре произведение давления газа на его объем постоянно.
Этот закон экспериментально был открыт английским ученым Р. Бойлем (1627-1691) и несколько позже французским ученым Э. Мариоттом (1620-1684). Поэтому он носит названиезакона Бойля - Мариотта.
Закон Бойля - Мариотта справедлив обычно для любых газов, а также и для их смесей, например для воздуха.
Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.
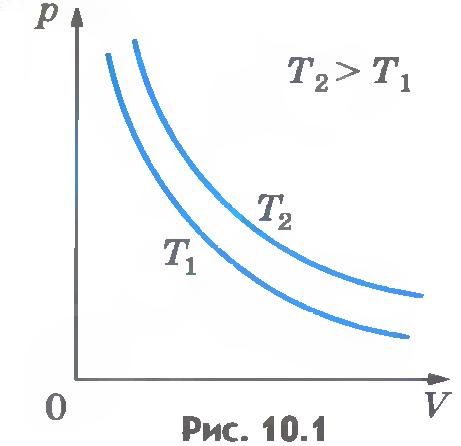
Зависимость давления газа от объема при постоянной температуре графически изображают кривой, которую называют изотермой. Изотерма газа изображает обратно пропорциональную зависимость между давлением и объемом. Кривую такого рода в математике называют гиперболой (рис.10.1).
Различным постоянным температурам соответствуют различные изотермы. При повышении температуры газа давление согласно уравнению состояния (10.4) увеличивается, если V=const. Поэтому изотерма, соответствующая более высокой температуре T2, лежит выше изотермы, соответствующей более низкой температуре T1 (см. рис.10.1).
Для того чтобы процесс происходил при постоянной температуре, сжатие или расширение газа должно происходить очень медленно. Дело в том, что, например, при сжатии газ нагревается, так как при движении поршня в сосуде скорость молекул после ударов о поршень увеличивается, а следовательно, увеличивается и температура газа. Именно поэтому для реализации изотермического процесса надо после небольшого смещения поршня подождать, когда температура газа в сосуде опять станет равной температуре окружающего воздуха.
Кроме этого, отметим, что при быстром сжатии давление под поршнем сразу становится больше, чем во всем сосуде. Если значения давления и температуры в различных точках объема разные, то в этом случае газ находится в неравновесном состоянии и мы не можем назвать значения температуры и давления, определяющие в данный момент состояние системы. Если систему предоставить самой себе, то температура и давление постепенно выравниваются, система приходит в равновесное состояние. Равновесное состояние - это состояние, при котором температура и давление во всех точках объема одинаковы. Параметры состояния газа могут быть определены, если он находится в равновесном состоянии. Процесс, при котором все промежуточные состояния газа являются равновесными, называют равновесным процессом. Очевидно, что на графиках зависимости одного параметра от другого мы можем изображать только равновесные процессы.
Изобарный процесс. Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным (от греческого слова «барос» - вес).
Согласно уравнению (10.4) в любом состоянии газа с неизменным давлением отношение объема газа к его температуре остается постоянным:
Для газа данной массы при постоянном давлении отношение объема к температуре постоянно.
Этот закон был установлен экспериментально в 1802 г. французским ученым Ж. Гей-Люссаком (1778-1850) и носит название закона Гей-Люссака. Согласно уравнению (10.7) объем газа при постоянном давлении пропорционален температуре:
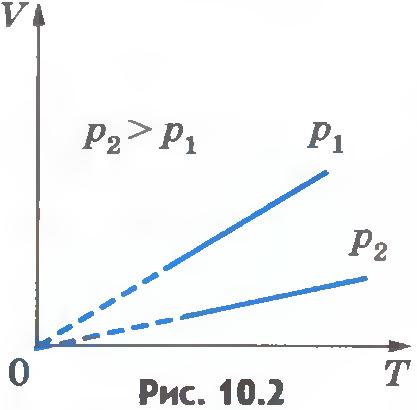
Эта зависимость графически изображается прямой, которая называется изобарой (рис.10.2). Разным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре согласно закону Бойля - Мариотта уменьшается. Поэтому изобара, соответствующая более высокому давлению p2, лежит ниже изобары, соответствующей более низкому давлению p1.
В области низких температур все изобары идеального газа сходятся в точке T=0. Но это не означает, что объем реального газа обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния (10.4) неприменимо. Именно поэтому, начиная с некоторого значения температуры, зависимость объема от температуры проводится на графике штриховой линией. В действительности таких значений температуры и давления у вещества в газообразном состоянии быть не может.
Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем, если внешнее давление постоянно. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня.
Изохорный процесс. Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным (от греческого слова «хорема» - вместимость).
Из уравнения состояния (10.4) вытекает, что в любом состоянии газа с неизменным объемом отношение давления газа к его температуре остается постоянным:
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
Этот газовый закон был установлен в 1787 г. французским физиком Ж.Шарлем (1746-1823) и носит название закона Шарля. Согласно уравнению (10.9) давление газа при постоянном объеме пропорционально температуре:
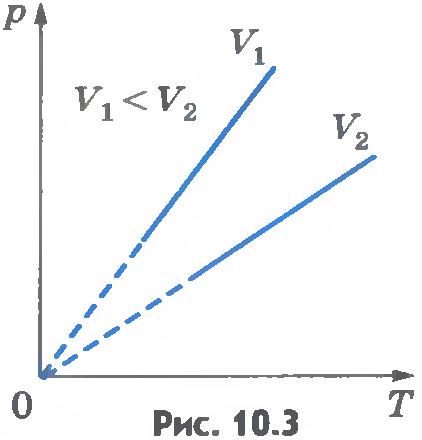
Эта зависимость изображается прямой, называемой изохорой (рис.10.3). Разным объемам соответствуют разные изохоры. С ростом объема газа при постоянной температуре давление его согласно закону Бойля - Мариотта падает. Поэтому изохора, соответствующая большему объему V2, лежит ниже изохоры, соответствующей меньшему объему V1.
В соответствии с уравнением (10.10) все изохоры идеального газа начинаются в точке T=0. Значит, давление идеального газа при абсолютном нуле равно нулю.
Увеличение давления газа в любом сосуде или в электрической лампочке при нагревании можно считать изохорным процессом. Изохорный процесс используется в газовых термометрах постоянного объема.
Газовые законы - частный случай уравнения состояния идеального газа, один из параметров которого остается постоянным.
???
1. Вы надули щеки. При этом и объем и давление воздуха у вас во рту увеличиваются. Как это согласовать с законом Бойля – Мариотта?
2. Как можно осуществить изотермический, изобарный и изохорный процессы?
3. Какое состояние системы (газа) считается равновесным?
4. Как качественно объяснить газовые законы на основе молекулярно-кинетической теории?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 10 класса
Содержание урока
 конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
