Презентация урока: Другие позиционные системы счисления

KNOWLEDGE HYPERMARKET

 		Версия 12:03, 31 октября 2012 (просмотреть исходный код)
User2  (Обсуждение | вклад)
 (Новая страница: «Презентация урока к предмету Информатика, 6 класс  '''''...»)
← Предыдущая правка
		Текущая версия на 12:04, 31 октября 2012 (просмотреть исходный код)
User2  (Обсуждение | вклад) 
м
 
		
Строка 1:
Строка 1:
- Презентация урока к предмету [[Информатика|Информатика]], [[Информатика_6_класс|6 класс]] + Презентация урока к предмету [[Информатика|Информатика]], [[Информатика 6 класс|6 класс]]  
  
- '''''Тема: «'''''[[Другие_позиционные_системы_счисления|'''''Другие позиционные системы счисления''''']]'''''»''''' + '''''Тема: «'''''[[Другие позиционные системы счисления|'''''Другие позиционные системы счисления''''']]'''''»'''''  
  
- <br> Неудобство использования двоичной системы счисления заключается в громоздкости записи чисел. Это неудобство не имеет существенного значения для ЭВМ. <br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; <br>Однако если возникает необходимость кодировать информацию «вручную», например, при составлении программы на машинном языке, то предпочтительнее оказывается пользоваться восьмеричной или шестнадцатеричной системой&nbsp; счисления.<br><br>Восьмеричная система счисления&nbsp;— позиционная&nbsp;целочисленная&nbsp;система счисления&nbsp;с основанием&nbsp;8. Для представления чисел в ней используются цифры от&nbsp;0&nbsp;до&nbsp;7. + <br> Неудобство использования двоичной системы счисления заключается в громоздкости записи чисел. Это неудобство не имеет существенного значения для ЭВМ. <br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; <br>Однако если возникает необходимость кодировать информацию «вручную», например, при составлении программы на машинном языке, то предпочтительнее оказывается пользоваться восьмеричной или шестнадцатеричной системой&nbsp; счисления.<br><br>Восьмеричная система счисления&nbsp;— позиционная&nbsp;целочисленная&nbsp;система счисления&nbsp;с основанием&nbsp;8. Для представления чисел в ней используются цифры от&nbsp;0&nbsp;до&nbsp;7.  
  
  + <br> 
  
  + [[Image:01 vojcekhovsky okt12-1.jpg]]<br> 
  
- [[Image:01_vojcekhovsky_okt12-1.jpg]]<br> + Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводомвосьмеричных чисел в&nbsp;двоичные&nbsp;и обратно, путём замены восьмеричных чисел на триплеты <br>двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена&nbsp;шестнадцатеричной. 
  
- Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводомвосьмеричных чисел в&nbsp;двоичные&nbsp;и обратно, путём замены восьмеричных чисел на триплеты <br>двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена&nbsp;шестнадцатеричной. + <br>  
  
  + При переводе из 2-ой в 8-уюсистему счисления надо число разбить на триады (по три разряда) и записать каждую триаду эквивалентным двоичным кодом, недостающее число разрядов надо дополнить слева нулями. <br> 
  
  + Примеры: <br>100111101<sub>2</sub>&nbsp;= 100111101<sub>2</sub>&nbsp;=475<sub>8</sub><br>1100010<sub>2</sub>&nbsp;= 001 100 010<sub>2</sub>&nbsp;=142<sub>8</sub> 
  
- При переводе из 2-ой в 8-уюсистему счисления надо число разбить на триады (по три разряда) и записать каждую триаду эквивалентным двоичным кодом, недостающее число разрядов надо дополнить слева нулями. <br> + <br>[[Image:01 vojcekhovsky okt12-2.jpg]] 
  
- Примеры: <br>100111101<sub>2</sub>&nbsp;= 100111101<sub>2</sub>&nbsp;=475<sub>8</sub><br>1100010<sub>2</sub>&nbsp;= 001 100 010<sub>2</sub>&nbsp;=142<sub>8</sub> + <br>  
  
- <br>[[Image:01_vojcekhovsky_okt12-2.jpg]] + <br>Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. <br>Например: <br>2541<sub>8</sub>&nbsp;= [ 2<sub>8</sub>&nbsp;| 5<sub>8</sub>&nbsp;| 4<sub>8</sub>&nbsp;| 1<sub>8</sub>&nbsp;] = <br>[010<sub>2</sub>&nbsp;| 101<sub>2</sub>&nbsp;| 100<sub>2</sub>&nbsp;|001<sub>2</sub>&nbsp;] = 010101100001<sub>2</sub><br> 
  
  + Двенадцатеричная система<br><br>Счет группами в 12 был в древности очень распространенным. Вспомним например, унции и двенадцатеричные дроби римлян.<br>Вместо десятков применяли при счете дюжины, то есть группы из двенадцати предметов. Во многих странах даже теперь некоторые товары, например вилки, ножи, ложки, продают дюжинами. Поэтому о человеке, не похожем на остальных, говорят "недюжинный".<br><br>А еще в начале двадцатого века в торговле применяли и дюжину дюжин, которую называли "гроссом", то есть "большойдюжиной", и даже дюжину гроссов- "массу". Так что пересчитав предметы в двенадцатеричной системе, можно было сказать: пять гроссов, восемь дюжин и еще шесть предметов.<br> 
  
  + Древние люди давно знали путь, который проходит солнце за год по звездному небу. Когда они разделили год на 12 месяцев, то каждую часть этого пути назвали "домом солнца", а звезды в этих домах объединили в созвездия. Так возникли созвездия Зодиака (большинство названийэтих созвездий происходит от имен животных).В Африке&nbsp; существуют народы, которые до сих пор ведут счет&nbsp;дюжинами.<br> 
  
- <br>Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. <br>Например: <br>2541<sub>8</sub>&nbsp;= [ 2<sub>8</sub>&nbsp;| 5<sub>8</sub>&nbsp;| 4<sub>8</sub>&nbsp;| 1<sub>8</sub>&nbsp;] = <br>[010<sub>2</sub>&nbsp;| 101<sub>2</sub>&nbsp;| 100<sub>2</sub>&nbsp;|001<sub>2</sub>&nbsp;] = 010101100001<sub>2</sub><br> + [[Image:01 vojcekhovsky okt12-3.jpg]]<br>  
-   + 
- Двенадцатеричная система<br><br>Счет группами в 12 был в древности очень распространенным. Вспомним например, унции и двенадцатеричные дроби римлян.<br>Вместо десятков применяли при счете дюжины,�то есть группы из двенадцати предметов. Во многих странах даже теперь некоторые товары, например вилки, ножи, ложки, продают дюжинами. Поэтому о человеке, не похожем на остальных, говорят "недюжинный".<br><br>А еще в начале двадцатого века в торговле применяли и дюжину дюжин, которую называли "гроссом", то есть "большойдюжиной", и даже дюжину гроссов- "массу". Так что пересчитав предметы в двенадцатеричной системе, можно было сказать: пять гроссов, восемь дюжин и еще шесть предметов.<br> + 
-   + 
- Древние люди давно знали путь, который проходит солнце за год по звездному небу. Когда они разделили год на 12 месяцев, то каждую часть этого пути назвали "домом солнца", а звезды в этих домах объединили в созвездия. Так возникли созвездия Зодиака (большинство названийэтих созвездий происходит от имен животных).В Африке&nbsp; существуют народы, которые до сих пор ведут счет&nbsp;дюжинами.<br> + 
-   + 
- [[Image:01_vojcekhovsky_okt12-3.jpg]]<br> + 
-   + 
  
  + <br> 
  
 Скачать полную презентацию урока можно нажав на текст [http://school.xvatit.com/Presentation/Gipermarket_october_2012/Informatiki_Pastuh_okt2012/Vojsehovskij/Rus/6kl_Т4.10_inf_3prez.ppt Скачать презентацию урока] и установив Microsoft PowerPoint    Скачать полную презентацию урока можно нажав на текст [http://school.xvatit.com/Presentation/Gipermarket_october_2012/Informatiki_Pastuh_okt2012/Vojsehovskij/Rus/6kl_Т4.10_inf_3prez.ppt Скачать презентацию урока] и установив Microsoft PowerPoint  
  
- <br> '''''Прислано учителем-участником Гильдии Лидеров образования Войцеховским''''' + <br> '''''Прислано учителем-участником Гильдии Лидеров образования Войцеховским'''''  
  
 [[Category:Другие_позиционные_системы_счисления._Презентация_урока]]  [[Category:Другие_позиционные_системы_счисления._Презентация_урока]]
Текущая версия на 12:04, 31 октября 2012
Презентация урока к предмету Информатика, 6 класс 
Тема: «Другие позиционные системы счисления» 

 Неудобство использования двоичной системы счисления заключается в громоздкости записи чисел. Это неудобство не имеет существенного значения для ЭВМ. 
      
Однако если возникает необходимость кодировать информацию «вручную», например, при составлении программы на машинном языке, то предпочтительнее оказывается пользоваться восьмеричной или шестнадцатеричной системой  счисления.

Восьмеричная система счисления — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7. 

 

 
Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводомвосьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты 
двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной. 

 
При переводе из 2-ой в 8-уюсистему счисления надо число разбить на триады (по три разряда) и записать каждую триаду эквивалентным двоичным кодом, недостающее число разрядов надо дополнить слева нулями. 
 
Примеры: 
100111101₂ = 100111101₂ =475₈
1100010₂ = 001 100 010₂ =142₈ 

 

 

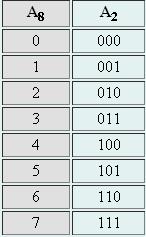
Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. 
Например: 
2541₈ = [ 2₈ | 5₈ | 4₈ | 1₈ ] = 
[010₂ | 101₂ | 100₂ |001₂ ] = 010101100001₂
 
Двенадцатеричная система

Счет группами в 12 был в древности очень распространенным. Вспомним например, унции и двенадцатеричные дроби римлян.
Вместо десятков применяли при счете дюжины, то есть группы из двенадцати предметов. Во многих странах даже теперь некоторые товары, например вилки, ножи, ложки, продают дюжинами. Поэтому о человеке, не похожем на остальных, говорят "недюжинный".

А еще в начале двадцатого века в торговле применяли и дюжину дюжин, которую называли "гроссом", то есть "большойдюжиной", и даже дюжину гроссов- "массу". Так что пересчитав предметы в двенадцатеричной системе, можно было сказать: пять гроссов, восемь дюжин и еще шесть предметов.
 
Древние люди давно знали путь, который проходит солнце за год по звездному небу. Когда они разделили год на 12 месяцев, то каждую часть этого пути назвали "домом солнца", а звезды в этих домах объединили в созвездия. Так возникли созвездия Зодиака (большинство названийэтих созвездий происходит от имен животных).В Африке  существуют народы, которые до сих пор ведут счет дюжинами.
 

 

 
Скачать полную презентацию урока можно нажав на текст Скачать презентацию урока и установив Microsoft PowerPoint 

 Прислано учителем-участником Гильдии Лидеров образования Войцеховским

Источник — «http://edufuture.biz/index.php?title=%D0%9F%D1%80%D0%B5%D0%B7%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D0%B8%D1%8F_%D1%83%D1%80%D0%BE%D0%BA%D0%B0:_%D0%94%D1%80%D1%83%D0%B3%D0%B8%D0%B5_%D0%BF%D0%BE%D0%B7%D0%B8%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D0%B5_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F»
Предмети > Информатика > Информатика 6 класс > Другие позиционные системы счисления > Другие позиционные системы счисления. Презентация урока
@@ Строка 1: / Строка 1: @@
-Презентация урока к предмету [[Информатика|Информатика]], [[Информатика_6_класс|6 класс]]
+Презентация урока к предмету [[Информатика|Информатика]], [[Информатика 6 класс|6 класс]]
-'''''Тема: «'''''[[Другие_позиционные_системы_счисления|'''''Другие позиционные системы счисления''''']]'''''»'''''
+'''''Тема: «'''''[[Другие позиционные системы счисления|'''''Другие позиционные системы счисления''''']]'''''»'''''
 <br> Неудобство использования двоичной системы счисления заключается в громоздкости записи чисел. Это неудобство не имеет существенного значения для ЭВМ. <br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; <br>Однако если возникает необходимость кодировать информацию «вручную», например, при составлении программы на машинном языке, то предпочтительнее оказывается пользоваться восьмеричной или шестнадцатеричной системой&nbsp; счисления.<br><br>Восьмеричная система счисления&nbsp;— позиционная&nbsp;целочисленная&nbsp;система счисления&nbsp;с основанием&nbsp;8. Для представления чисел в ней используются цифры от&nbsp;0&nbsp;до&nbsp;7.
+<br>
+[[Image:01 vojcekhovsky okt12-1.jpg]]<br>
-[[Image:01_vojcekhovsky_okt12-1.jpg]]<br>
+Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводомвосьмеричных чисел в&nbsp;двоичные&nbsp;и обратно, путём замены восьмеричных чисел на триплеты <br>двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена&nbsp;шестнадцатеричной.
-Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводомвосьмеричных чисел в&nbsp;двоичные&nbsp;и обратно, путём замены восьмеричных чисел на триплеты <br>двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена&nbsp;шестнадцатеричной.
+<br>
+При переводе из 2-ой в 8-уюсистему счисления надо число разбить на триады (по три разряда) и записать каждую триаду эквивалентным двоичным кодом, недостающее число разрядов надо дополнить слева нулями. <br>
+Примеры: <br>100111101<sub>2</sub>&nbsp;= 100111101<sub>2</sub>&nbsp;=475<sub>8</sub><br>1100010<sub>2</sub>&nbsp;= 001 100 010<sub>2</sub>&nbsp;=142<sub>8</sub>
-При переводе из 2-ой в 8-уюсистему счисления надо число разбить на триады (по три разряда) и записать каждую триаду эквивалентным двоичным кодом, недостающее число разрядов надо дополнить слева нулями. <br>
+<br>[[Image:01 vojcekhovsky okt12-2.jpg]]
-Примеры: <br>100111101<sub>2</sub>&nbsp;= 100111101<sub>2</sub>&nbsp;=475<sub>8</sub><br>1100010<sub>2</sub>&nbsp;= 001 100 010<sub>2</sub>&nbsp;=142<sub>8</sub>
+<br>
-<br>[[Image:01_vojcekhovsky_okt12-2.jpg]]
+<br>Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. <br>Например: <br>2541<sub>8</sub>&nbsp;= [ 2<sub>8</sub>&nbsp;| 5<sub>8</sub>&nbsp;| 4<sub>8</sub>&nbsp;| 1<sub>8</sub>&nbsp;] = <br>[010<sub>2</sub>&nbsp;| 101<sub>2</sub>&nbsp;| 100<sub>2</sub>&nbsp;|001<sub>2</sub>&nbsp;] = 010101100001<sub>2</sub><br>
+Двенадцатеричная система<br><br>Счет группами в 12 был в древности очень распространенным. Вспомним например, унции и двенадцатеричные дроби римлян.<br>Вместо десятков применяли при счете дюжины, то есть группы из двенадцати предметов. Во многих странах даже теперь некоторые товары, например вилки, ножи, ложки, продают дюжинами. Поэтому о человеке, не похожем на остальных, говорят "недюжинный".<br><br>А еще в начале двадцатого века в торговле применяли и дюжину дюжин, которую называли "гроссом", то есть "большойдюжиной", и даже дюжину гроссов- "массу". Так что пересчитав предметы в двенадцатеричной системе, можно было сказать: пять гроссов, восемь дюжин и еще шесть предметов.<br>
+Древние люди давно знали путь, который проходит солнце за год по звездному небу. Когда они разделили год на 12 месяцев, то каждую часть этого пути назвали "домом солнца", а звезды в этих домах объединили в созвездия. Так возникли созвездия Зодиака (большинство названийэтих созвездий происходит от имен животных).В Африке&nbsp; существуют народы, которые до сих пор ведут счет&nbsp;дюжинами.<br>
-<br>Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. <br>Например: <br>2541<sub>8</sub>&nbsp;= [ 2<sub>8</sub>&nbsp;| 5<sub>8</sub>&nbsp;| 4<sub>8</sub>&nbsp;| 1<sub>8</sub>&nbsp;] = <br>[010<sub>2</sub>&nbsp;| 101<sub>2</sub>&nbsp;| 100<sub>2</sub>&nbsp;|001<sub>2</sub>&nbsp;] = 010101100001<sub>2</sub><br>
+[[Image:01 vojcekhovsky okt12-3.jpg]]<br>
-Двенадцатеричная система<br><br>Счет группами в 12 был в древности очень распространенным. Вспомним например, унции и двенадцатеричные дроби римлян.<br>Вместо десятков применяли при счете дюжины,�то есть группы из двенадцати предметов. Во многих странах даже теперь некоторые товары, например вилки, ножи, ложки, продают дюжинами. Поэтому о человеке, не похожем на остальных, говорят "недюжинный".<br><br>А еще в начале двадцатого века в торговле применяли и дюжину дюжин, которую называли "гроссом", то есть "большойдюжиной", и даже дюжину гроссов- "массу". Так что пересчитав предметы в двенадцатеричной системе, можно было сказать: пять гроссов, восемь дюжин и еще шесть предметов.<br>
-Древние люди давно знали путь, который проходит солнце за год по звездному небу. Когда они разделили год на 12 месяцев, то каждую часть этого пути назвали "домом солнца", а звезды в этих домах объединили в созвездия. Так возникли созвездия Зодиака (большинство названийэтих созвездий происходит от имен животных).В Африке&nbsp; существуют народы, которые до сих пор ведут счет&nbsp;дюжинами.<br>
-[[Image:01_vojcekhovsky_okt12-3.jpg]]<br>
+<br>
 Скачать полную презентацию урока можно нажав на текст [http://school.xvatit.com/Presentation/Gipermarket_october_2012/Informatiki_Pastuh_okt2012/Vojsehovskij/Rus/6kl_Т4.10_inf_3prez.ppt Скачать презентацию урока] и установив Microsoft PowerPoint
 <br> '''''Прислано учителем-участником Гильдии Лидеров образования Войцеховским'''''
 [[Category:Другие_позиционные_системы_счисления._Презентация_урока]]

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: