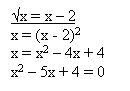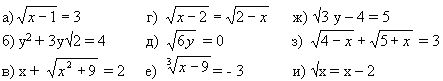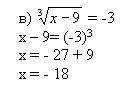Текущая версия на 17:32, 3 сентября 2015
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Иррациональные уравнения
Иррациональные уравненияСегодняшний наш урок будет посвящен изучению уравнений, у которых переменная стоит под знаком квадратного или другого корня. Мы с вами попробуем на примерах уравнений подробно разобраться и научиться правильно решать иррациональные уравнения. Естественно, в первую очередь нам необходимо выяснить, какие же уравнения являются иррациональными. Давайте для начала озвучим определение такого уравнения. Уравнения называются иррациональными, если их переменная стоит под знаком корня. А теперь давайте приведем примеры иррациональных уравнений и посмотрим, как они выглядят: Как решаются иррациональные уравненияКак правило, все иррациональные уравнения решаются в три этапа: • Во-первых, для начала необходимо уединить корень. Что это значит? То есть, если мы видим, что слева от знака равенства кроме корня есть еще и другие функции или числа, то в этом случае нам необходимо все это перенести вправо и поменять знак. Что же касается левой стороны, то здесь должен остаться лишь радикал и без всяких коэффициентов. • Во-вторых, нам необходимо возвести в квадрат обе части этого уравнения. Но здесь не мешало бы быть внимательными и помнить, что к области значения корня относятся все неотрицательные числа. Из этого следует, что в иррациональном уравнении функция, которая расположена справа, также должна быть неотрицательной: g(x) ≥ 0. • В-третьих, и это будет логично, необходимо выполнить проверку. А такая необходимость может возникнуть потому, что на втором этапе при решении уравнения у нас могли появиться лишние корни. А чтобы от этих корней избавиться, нам нужно полученные числа-кандидаты взять и подставить в исходное уравнение. Ну, а потом, естественно, нужно проверить, получилось ли на самом деле верное числовое равенство. Решение иррационального уравненияА теперь, на приведенном примере, который был дан вначале нашего урока, попробуем разобраться с таким иррациональным уравнением. Посмотрев на это уравнение, мы видим, что в нем корень уже уединен, так как слева от знака равенства, кроме корня мы больше ничего не наблюдаем. Теперь давайте возведем обе стороны этого уравнения в квадрат и смотрим, что в итоге у нас получится: 2x2 − 14x + 13 = (5 − x)2 Теперь, через дискриминант попробуем решить квадратное уравнение, которое у нас получилось: D = b2 − 4ac = (−4)2 − 4 • 1 • (−12) = 16 + 48 = 64; Вот мы с вами решили уравнение и теперь нам нужно всего лишь в исходное уравнение подставить полученные числа и таким образом выполнить его проверку. Конечно же, можно поступить, еще более обдумано и итоговое решение, взять и упростить. Как упростить решение?А теперь давайте попробуем ответить на вопрос, зачем нам необходимо в конце решения иррационального уравнения делать проверку? На этот вопрос, естественно вы ответите, что проверка необходима для того, чтобы мы могли быть уверены в том, что при выполнении подстановки наших корней с правой стороны от знака равенства, стоит неотрицательное число. Но ведь, нам и так известно, что в иррациональном уравнении арифметический квадратный корень уже по определению не может быть меньше нуля, поэтому число отрицательным также быть не может. Тогда возникает вопрос, что же, по сути, нам необходимо проверить? А все очень просто, нам нужно быть уверенными, что функция, которая стоит справа от знака равенства: g(x) = 5 − x, была, естественно, неотрицательной: g(x) ≥ 0 С этим мы выяснили, теперь давайте подставим наши корни в эту функцию и получим такой результат: g(x1) = g(6) = 5 − 6 = −1 < 0 И к какому мы выводу пришли? Подставив корни в функцию, мы видим, что корень x1 = 6 нам совершенно не подходит, так как, подставив его в правую часть исходного уравнения, у нас вышло отрицательное число. Тогда, когда корень x2 = −2 нас вполне устраивает, так как: • Во-первых, потому, что этот корень и есть решением квадратного уравнения, так как был получен при помощи возведения в квадрат обеих сторон иррационального уравнения. • Во-вторых, потому, что при подстановке корня x2 = −2, в итоге, правая сторона исходного иррационального уравнения имеет положительное число. А так как это число положительно, то значит, что и область значений арифметического корня не нарушена. Вот мы с вами и решили алгоритм. Теперь вы видите, что, оказывается, решать уравнения с радикалами, не представляет никакой сложности. При решении таких уравнений во избежание вероятности получения лишних ответов, главное никогда не забывать делать проверку полученных корней. Исторические факты о иррациональных величинахА известно ли вам, что в переводе с латыни такое слово, как «иррациональный» звучит, как «неразумный». Но еще интересен тот факт, что параллельно с термином «неразумный» или «иррациональный» математики средневековья иррациональные числа еще нарекали термином «surdus», что в переводе звучало, как «глухой» и «немой». Складывается такое впечатление, что ученые не сильно жаловали иррациональные числа, считая их чем-то «неразумным», что нельзя ни высказать, ни выслушать. Но, если поначалу математики Древнего мира практически отказывались воспринимать иррациональные числа, то со временем начали проявлять пристальное внимание к таким объектам математики. А знаете ли вы, что в период бурного развития математических наук и астрономии математики Индии, Ближнего и Среднего Востока, длительное время отвергали иррациональные числа, хотя практически не могли обходиться без иррациональных величин. А знаете ли вы, откуда появилось такое современное обозначение квадратного корня? Оказывается, начиная с тринадцатого века, длились эволюционные изменения знака радикала. Впервые название квадратному корню дали итальянские математики от латинского слова Radix, что в переводе обозначало корень, а его сокращенным вариантом была буква R. Домашнее заданиеИзучив тему иррациональных уравнений, выполните домашнее задание, решив данные уравнения, и дайте ответы на поставленные вопросы. 1. Решите данное уравнение: Ответьте на вопросы: • Как вы думаете, будет ли это уравнение иррациональным? 2. Решите данные уравнения и скажите, какие из них являются иррациональными? 3. Решите уравнение: Дайте ответы на поставленные вопросы: • Какое перед вами уравнение и является ли оно иррациональным? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: