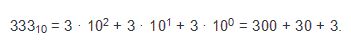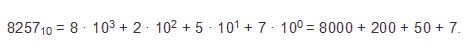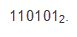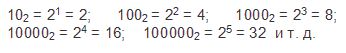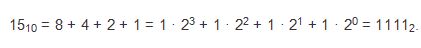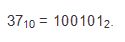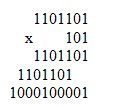|
|
|
| Строка 23: |
Строка 23: |
| | <h2>Десятичная и двоичная системы счисления</h2> | | <h2>Десятичная и двоичная системы счисления</h2> |
| | | | |
| - | ''Системой счисления называют определенные правила записи чисел и связанные с ними способы выполнения вычислений. ''
| + | Системой счисления или в сокращенном варианте СС называют такую систему записи чисел, которая имеет определенный набор цифр. |
| | | | |
| - | С историей систем счисления вы познакомитесь в главе 7 учебника. А пока нас будут интересовать двоичная и десятичная системы счисления.
| + | Об истории различных систем счисления вы узнали, когда изучали 7 главу учебника. А сегодня мы с вами обратим наше внимание на такие системы счисления, как двоичная и десятичная СС. |
| | | | |
| - | '''[[Другие позиционные системы счисления|Система счисления]]''', к которой мы все привыкли, называется десятичной. Объясняется это название тем, что в ней используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число цифр определяет основание системы счисления. Если число цифр — десять, то основание системы счисления равно десяти. В двоичной же системе существует всего две цифры: 0 и 1. Основание равно двум. Возникает вопрос, можно ли с помощью всего двух цифр представить любую величину. Оказывается, можно!
| + | Как вам уже известно из изученного ранее материала, что одной из наиболее часто применяемых систем счисления является десятичная СС. А называется эта система так потому, что в основе этого словообразования есть число 10. Вот поэтому и система счисления называется десятичной. |
| | | | |
| - | <h2>Развернутая форма записи числа</h2>
| + | Вы уже знаете, что в этой системе используют такие десять цифр, как 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. А вот числу десять отведена исключительная роль, так как на наших руках насчитывается десять пальцев. То есть, десять цифр являются основанием данной системы счисления. |
| | | | |
| - | Вспомним принцип записи чисел в десятичной системе счисления. Значение цифры в записи числа зависит не только от самой цифры, но и от места расположения этой цифры в числе (говорят: от позиции цифры). Например, в числе 333 первая справа цифра обозначает: три единицы, следующая — три десятка, следующая — три сотни. Этот факт можно выразить равенством:
| + | А вот в двоичной системе счисления, задействованные только две цифры, такие, как 0 и 1 и основанием этой системы является число 2. |
| | | | |
| - | 333<sub>10</sub> = 3 · 10<sup>2</sup> + 3 · 10<sup>1</sup> + 3 · 10<sup>0</sup> = 300 + 30 + 3.
| + | Теперь давайте попробуем разобраться, как с помощью всего лишь двух цифр представить какую-то величину. |
| | | | |
| - | В данном равенстве выражение, стоящее справа от знака «равно», называется развернутой формой записи многозначного числа. Вот еще пример развернутой формы записи многозначного десятичного числа:
| + | <h2>Развернутая форма записи числа</h2> |
| | | | |
| - | 8257<sub>10</sub> = 8 · 10<sup>3</sup> + 2 · 10<sup>2</sup> + 5 · 10<sup>1</sup> + 7 · 10<sup>0 </sup>= 8000 + 200 + 50 + 7.
| + | Давайте обратимся к своей памяти и вспомним, какой в десятичной СС существует принцип записи чисел. То есть, для вас уже не будет секретом, что в такой СС запись числа зависит от места расположения цифры, то есть, от ее позиции. |
| | | | |
| - | Таким образом, с продвижением от цифры к цифре справа налево «вес» каждой цифры увеличивается в 10 раз. Это связано с тем, что основание системы счисления равно десяти.
| + | Так, например, цифра, которая является крайней справа, говорит нам о количестве единиц этого числа, следующая за этой цифрой, как правило, указывает на количество двоек и т.д. |
| | | | |
| - | Перевод двоичных чисел в '''[[Десятичная система счисления|десятичную систему]]'''
| + | Если мы с вами, например, возьмем такое число, как 333, то увидим, что крайняя правая цифра обозначает три единицы, потом три десятка и за ней – три сотни. |
| | | | |
| - | А вот пример многозначного двоичного числа:
| + | Теперь это изобразим в виде такого равенства: |
| | | | |
| - | 110101<sub>2</sub>.
| + | <br> |
| | + | [[Image:9kl_Duo.Sist01.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | + | |
| | + | Здесь мы видим равенство, в котором выражение, расположенное с правой стороны от знака равно, предоставлено в виде развернутой формы записи этого многозначного числа. |
| | | | |
| - | Двойка внизу справа указывает на основание системы счисления. Это нужно для того, чтобы не перепутать двоичное число с десятичным. Ведь существует же десятичное число 110101! Вес каждой следующей цифры в двоичном числе при продвижении справа налево возрастает в 2 раза. Развернутая форма записи данного двоичного числа выглядит так:<br>
| + | Рассмотрим еще один пример многозначного десятичного числа, который также представлен в развернутой форме: |
| | + | |
| | + | <br> |
| | + | [[Image:9kl_Duo.Sist02.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | | | |
| - | 110101<sub>2</sub> = 1 · 2<sup>5 </sup>+ 1 · 2<sup>4</sup> + 0 · 2<sup>3</sup> + 1 · 2<sup>2</sup> + 0 · 2<sup>1</sup> + 1 · 2<sup>0</sup> = 53<sub>10</sub>.<br>
| + | Эти примеры нам показывают, что чем дальше мы движемся от цифры к цифре справа налево, то каждая цифра увеличивается в десять раз. А происходит это потому, что основание СС равно десяти. |
| | | | |
| - | Таким способом мы перевели двоичное число в десятичную систему.
| + | <h2>Перевод двоичных чисел в десятичную систему</h2> |
| | | | |
| - | Переведем в десятичную систему еще несколько двоичных чисел.
| + | Теперь давайте для примера возьмем такое многозначительное двоичное число, как: |
| | | | |
| - | 10<sub>2</sub> = 2<sup>1</sup> = 2; 100<sub>2 </sub>= 2<sup>2</sup> = 4; 1000<sub>2</sub> = 2<sup>3</sup> = 8;<br>10000<sub>2</sub> = 2<sup>4</sup> = 16; 100000<sub>2</sub> = 2<sup>5</sup> = 32 и т. д.
| + | <br> |
| | + | [[Image:9kl_Duo.Sist03.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | + | |
| | + | В этом многозначительном числе мы видим с правой стороны внизу двойку, которая нам указывает на основание системы счисления. То есть, нам понятно, что перед нами двоичное число и перепутать его с десятичным, мы уже не можем. |
| | | | |
| - | Таким образом, получилось, что двузначному десятичному числу соответствует шестизначное двоичное! И это характерно для двоичной системы: быстрый рост количества цифр с увеличением значения числа.
| + | И значение каждой следующей цифры в двоичном числе возрастает в 2 раза при каждом шаге справа налево. Теперь давайте посмотрим, как будет выглядеть развернутая форма записи этого двоичного числа: |
| | | | |
| - | Вот как выглядит начало натурального ряда чисел в десятичной (А<sub>10</sub>) и двоичной (А<sub>2</sub>) системах счисления: <br>
| + | <br> |
| | + | [[Image:9kl_Duo.Sist04.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | + | |
| | + | На этом примере мы видим, как можно перевести перевели двоичное число в десятичную систему. |
| | | | |
| - | {| width="500" cellspacing="1" cellpadding="1" border="1"
| + | Теперь давайте еще приведем несколько примеров перевода двоичных чисел в десятичную систему счисления: |
| - | |-
| + | |
| - | | A<sub>10</sub><br>
| + | |
| - | | 1<br>
| + | |
| - | | 2<br>
| + | |
| - | | 3<br>
| + | |
| - | | 4<br>
| + | |
| - | | 5<br>
| + | |
| - | | 6<br>
| + | |
| - | | 7<br>
| + | |
| - | | 8<br>
| + | |
| - | | 9<br>
| + | |
| - | | 10<br>
| + | |
| - | |-
| + | |
| - | | A<sub>2</sub><br>
| + | |
| - | | 1<br>
| + | |
| - | | 10<br>
| + | |
| - | | 11<br>
| + | |
| - | | 100<br>
| + | |
| - | | 101<br>
| + | |
| - | | 110<br>
| + | |
| - | | 111<br>
| + | |
| - | | 1000<br>
| + | |
| - | | 1001<br>
| + | |
| - | | 1010<br>
| + | |
| - | |}
| + | |
| | | | |
| - | <br> | + | <br> |
| | + | [[Image:9kl_Duo.Sist05.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | + | |
| | + | Это пример нам показывает то, что двузначному десятичному числу, в данном случае, соответствует шестизначное двоичное. Для двоичной системы характерно такое возрастание количества цифр при увеличении значения числа. |
| | | | |
| - | {| width="500" cellspacing="1" cellpadding="1" border="1"
| + | А теперь давайте посмотрим, как будет выглядеть начало натурального ряда чисел в десятичной (А10) и двоичной (А2) СС: |
| - | |-
| + | |
| - | | A<sub>10</sub>
| + | |
| - | | 11
| + | |
| - | | 12
| + | |
| - | | 13
| + | |
| - | | 14
| + | |
| - | | 15
| + | |
| - | | 16
| + | |
| - | | 17
| + | |
| - | | 18
| + | |
| - | | 19
| + | |
| - | | 20
| + | |
| - | |-
| + | |
| - | | A<sub>2</sub>
| + | |
| - | | 1011
| + | |
| - | | 1100
| + | |
| - | | 1101
| + | |
| - | | 1110
| + | |
| - | | 1111
| + | |
| - | | 10000
| + | |
| - | | 10001
| + | |
| - | | 10010
| + | |
| - | | 10011
| + | |
| - | | 10100
| + | |
| - | |}
| + | |
| | | | |
| | + | <br> |
| | + | [[Image:9kl_Duo.Sist06.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | + | |
| | + | <h2>Перевод десятичных чисел в двоичную систему</h2> |
| | | | |
| - | <h2>Перевод десятичных чисел в двоичную систему</h2>
| + | Рассмотрев приведенные примеры выше, надеюсь вам теперь понятно, как происходит перевод двоичного числа в равное десятичное число. Ну, а теперь давайте попробуем сделать обратный перевод. Смотрим, что нам для этого необходимо сделать. Нам для такого перевода необходимо попробовать разложить десятичное число на слагаемые, которые представляют собой степени двойки. Приведем такой пример: |
| | | | |
| - | Как перевести двоичное число в равное ему десятичное, вам должно быть понятно из рассмотренных выше примеров. А как осуществить обратный перевод: из десятичной системы в двоичную? Для этого нужно суметь разложить десятичное число на слагаемые, представляющие собой степени двойки. Например:<br> | + | <br> |
| | + | [[Image:9kl_Duo.Sist07.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | + | |
| | + | Как видим, это сделать не так уж и просто. Давайте попробуем рассмотреть другой, более простой метод перевода из десятичной СС в двоичную. Такой метод состоит в том, что известное десятичное число, как правило, делиться на два, а его полученный остаток и будет выступать младшим разрядом искомого числа. Это, вновь полученное число мы снова делим на два и получаем следующий разряд искомого числа. Такой процесс деления мы будем продолжать до тех пор, пока частное не станет меньше основания двоичной системы, то есть, меньше двойки. Вот такое полученное частное и будет старшей цифрой числа, которое мы искали. |
| | | | |
| - | 15<sub>10</sub> = 8 + 4 + 2 + 1 = 1 · 2<sup>3</sup> + 1 · 2<sup>2</sup> + 1 · 2<sup>1</sup> + 1 · 2<sup>0</sup> = 1111<sub>2</sub>.<br>
| + | Давайте теперь рассмотрим методы записи деления на число два. Для примера возьмем |
| | + | число 37 и попробуем его перевести в двоичную систему. |
| | | | |
| - | Это сложно. Есть другой способ, с которым мы сейчас и познакомимся.<br>
| + | <br> |
| - | | + | [[Image:9kl_Duo.Sist08.jpg|500x500px|двоичная сист.]] |
| - | Существует процедура, позволяющая легко выполнить перевод десятичного числа в двоичную систему. Она состоит в том, что данное десятичное число делится на 2. Полученный остаток — это младший разряд искомого числа. Полученное частное снова делится на 2, полученный при этом остаток — это следующий разряд искомого числа. Так продолжается до тех пор, пока частное не станет меньше двойки (основания системы). Это частное — старшая цифра искомого числа.<br>
| + | <br> |
| - | | + | |
| - | Существуют два способа записи деления на 2. Продемонстрируем это на примере перевода числа 37 в двоичную систему.
| + | На данных примерах мы видим, что а5, а4, а3, а2, а1, а0 являются обозначением цифр в записи двоичного числа, которые осуществляются по порядку слева направо. В итоге мы с вами получим: |
| - | | + | |
| - | [[Image:Informatika 9 102z.jpg|480px|Перевода числа 37 в двоичную систему. ]]<br> | + | |
| - | | + | |
| - | Здесь а<sub>5</sub>, а<sub>4</sub>, а<sub>3</sub>, а<sub>2</sub>, а<sub>1</sub>, а<sub>0</sub> — обозначения цифр в записи двоичного числа по порядку слева направо. В результате перевода получим: 37<sub>10</sub> = 100101<sub>2</sub>. <br>
| + | |
| | | | |
| | + | <br> |
| | + | [[Image:9kl_Duo.Sist09.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | + | |
| | <h2>Арифметика двоичных чисел</h2> | | <h2>Арифметика двоичных чисел</h2> |
| | | | |
| - | Правила двоичной арифметики гораздо проще правил десятичной арифметики. Вот все возможные варианты сложения и умножения однозначных двоичных чисел.
| + | Если исходить из правил в арифметике, то легко заметить, что в двоичной системе счислений, они намного проще, чем в десятичной. |
| - | | + | |
| - | 0 + 0 = 0 0 x 0 = 0<br>0 + 1 = 1 0 x 1 = 0<br>1 + 0 = 1 1 x 0 = 0 <br>1 + 1 = 10 1 x 1 = 1
| + | |
| - | | + | |
| - | Своей простотой и согласованностью с битовой структурой компьютерной памяти двоичная система счисления и привлекла изобретателей компьютера. Ее гораздо проще реализовать техническими средствами, чем десятичную систему.
| + | |
| | | | |
| - | Вот пример сложения столбиком двух многозначных двоичных чисел:
| + | Теперь давайте вспомним варианты сложения и умножения однозначных двоичных чисел. |
| | | | |
| - | 1011011101<br> +<u>111010110</u><br>10010110011
| + | <br> |
| | + | [[Image:9kl_Duo.Sist10.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | + | |
| | + | Благодаря такой простоте, которая легко согласовывается с битовой структурой компьютерной памяти, двоичная система счисления привлекла внимание создателей компьютера. |
| | | | |
| - | А теперь посмотрите внимательно на следующий пример умножения многозначных двоичных чисел:
| + | Обратите внимание на то, как выполняется пример сложения двух многозначных двоичных чисел при помощи столбика: |
| | | | |
| - | 1101101<br> x <u> 101</u><br> 1101101<br><u> 1101101</u><br>1000100001
| + | <br> |
| | + | [[Image:9kl_Duo.Sist11.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | + | |
| | + | А вот перед вами пример умножения многозначных двоичных чисел в столбик: |
| | | | |
| - | После небольшой тренировки любой из вас такие вычисления будет выполнять автоматически.
| + | <br> |
| | + | [[Image:9kl_Duo.Sist12.jpg|500x500px|двоичная сист.]] |
| | + | <br> |
| | + | |
| | + | Вы заметили, как легко и просто выполнять такие примеры. |
| | | | |
| | <h2>Коротко о главном</h2> | | <h2>Коротко о главном</h2> |
Версия 16:49, 19 сентября 2015
Гипермаркет знаний>>Информатика>>Информатика 9 класс>>Информатика: Двоичная система счисления
План урока
Здесь вы узнаете:
♦ как компьютер работает с числами;
♦ что такое электронная таблица;
♦ как решаются вычислительные задачи;
♦ с помощью электронных таблиц;
♦ как можно использовать электронные таблицы для информационного моделирования.
Двоичная система счисления
Основные темы параграфа:
♦ десятичная и двоичная системы счисления;
♦ развернутая форма записи числа;
♦ перевод двоичных чисел в десятичную систему;
♦ перевод десятичных чисел в двоичную систему;
♦ арифметика двоичных чисел.
В данной главе речь пойдет об организации вычислений на компьютере. Вычисления связаны с хранением и обработкой чисел.
Компьютер работает с числами в двоичной системе счисления.
Эта идея принадлежит Джону фон Нейману, сформулировавшему в 1946 году принципы устройства и работы ЭВМ. Выясним, что такое система счисления.
Десятичная и двоичная системы счисления
Системой счисления или в сокращенном варианте СС называют такую систему записи чисел, которая имеет определенный набор цифр.
Об истории различных систем счисления вы узнали, когда изучали 7 главу учебника. А сегодня мы с вами обратим наше внимание на такие системы счисления, как двоичная и десятичная СС.
Как вам уже известно из изученного ранее материала, что одной из наиболее часто применяемых систем счисления является десятичная СС. А называется эта система так потому, что в основе этого словообразования есть число 10. Вот поэтому и система счисления называется десятичной.
Вы уже знаете, что в этой системе используют такие десять цифр, как 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. А вот числу десять отведена исключительная роль, так как на наших руках насчитывается десять пальцев. То есть, десять цифр являются основанием данной системы счисления.
А вот в двоичной системе счисления, задействованные только две цифры, такие, как 0 и 1 и основанием этой системы является число 2.
Теперь давайте попробуем разобраться, как с помощью всего лишь двух цифр представить какую-то величину.
Развернутая форма записи числа
Давайте обратимся к своей памяти и вспомним, какой в десятичной СС существует принцип записи чисел. То есть, для вас уже не будет секретом, что в такой СС запись числа зависит от места расположения цифры, то есть, от ее позиции.
Так, например, цифра, которая является крайней справа, говорит нам о количестве единиц этого числа, следующая за этой цифрой, как правило, указывает на количество двоек и т.д.
Если мы с вами, например, возьмем такое число, как 333, то увидим, что крайняя правая цифра обозначает три единицы, потом три десятка и за ней – три сотни.
Теперь это изобразим в виде такого равенства:
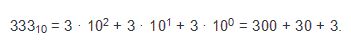
Здесь мы видим равенство, в котором выражение, расположенное с правой стороны от знака равно, предоставлено в виде развернутой формы записи этого многозначного числа.
Рассмотрим еще один пример многозначного десятичного числа, который также представлен в развернутой форме:
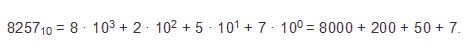
Эти примеры нам показывают, что чем дальше мы движемся от цифры к цифре справа налево, то каждая цифра увеличивается в десять раз. А происходит это потому, что основание СС равно десяти.
Перевод двоичных чисел в десятичную систему
Теперь давайте для примера возьмем такое многозначительное двоичное число, как:
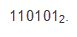
В этом многозначительном числе мы видим с правой стороны внизу двойку, которая нам указывает на основание системы счисления. То есть, нам понятно, что перед нами двоичное число и перепутать его с десятичным, мы уже не можем.
И значение каждой следующей цифры в двоичном числе возрастает в 2 раза при каждом шаге справа налево. Теперь давайте посмотрим, как будет выглядеть развернутая форма записи этого двоичного числа:
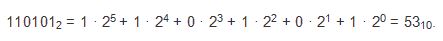
На этом примере мы видим, как можно перевести перевели двоичное число в десятичную систему.
Теперь давайте еще приведем несколько примеров перевода двоичных чисел в десятичную систему счисления:
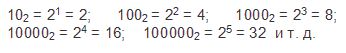
Это пример нам показывает то, что двузначному десятичному числу, в данном случае, соответствует шестизначное двоичное. Для двоичной системы характерно такое возрастание количества цифр при увеличении значения числа.
А теперь давайте посмотрим, как будет выглядеть начало натурального ряда чисел в десятичной (А10) и двоичной (А2) СС:
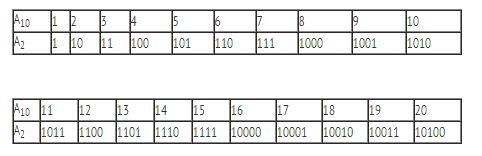
Перевод десятичных чисел в двоичную систему
Рассмотрев приведенные примеры выше, надеюсь вам теперь понятно, как происходит перевод двоичного числа в равное десятичное число. Ну, а теперь давайте попробуем сделать обратный перевод. Смотрим, что нам для этого необходимо сделать. Нам для такого перевода необходимо попробовать разложить десятичное число на слагаемые, которые представляют собой степени двойки. Приведем такой пример:
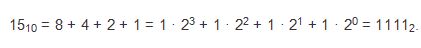
Как видим, это сделать не так уж и просто. Давайте попробуем рассмотреть другой, более простой метод перевода из десятичной СС в двоичную. Такой метод состоит в том, что известное десятичное число, как правило, делиться на два, а его полученный остаток и будет выступать младшим разрядом искомого числа. Это, вновь полученное число мы снова делим на два и получаем следующий разряд искомого числа. Такой процесс деления мы будем продолжать до тех пор, пока частное не станет меньше основания двоичной системы, то есть, меньше двойки. Вот такое полученное частное и будет старшей цифрой числа, которое мы искали.
Давайте теперь рассмотрим методы записи деления на число два. Для примера возьмем
число 37 и попробуем его перевести в двоичную систему.
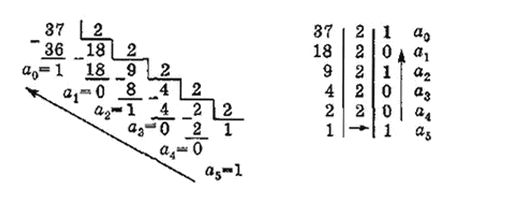
На данных примерах мы видим, что а5, а4, а3, а2, а1, а0 являются обозначением цифр в записи двоичного числа, которые осуществляются по порядку слева направо. В итоге мы с вами получим:
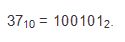
Арифметика двоичных чисел
Если исходить из правил в арифметике, то легко заметить, что в двоичной системе счислений, они намного проще, чем в десятичной.
Теперь давайте вспомним варианты сложения и умножения однозначных двоичных чисел.

Благодаря такой простоте, которая легко согласовывается с битовой структурой компьютерной памяти, двоичная система счисления привлекла внимание создателей компьютера.
Обратите внимание на то, как выполняется пример сложения двух многозначных двоичных чисел при помощи столбика:

А вот перед вами пример умножения многозначных двоичных чисел в столбик:
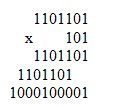
Вы заметили, как легко и просто выполнять такие примеры.
Коротко о главном
Система счисления — определенные правила записи чисел и связанные с этими правилами способы выполнения вычислений.
Основание системы счисления равно количеству используемых в ней цифр.
Двоичные числа — числа в двоичной системе счисления. В их записи используются две цифры: 0 и 1.
Развернутая форма записи двоичного числа — это его представление в виде суммы степеней двойки, умноженных на 0 или на 1.
Использование двоичных чисел в компьютере связано с битовой структурой компьютерной памяти и простотой двоичной арифметики.
Достоинства двоичной системы счисления
А теперь давайте рассмотрим, какими достоинствами обладает двоичная система исчисления:
• Во-первых, достоинством двоичной системы счисления является то, что с ее помощью довольно таки просто осуществлять процессы хранения, передачи и обработки информации на компьютере.
• Во-вторых, для ее выполнения достаточно не десять элементов, а лишь два;
• В-третьих, отображение информации с помощью лишь двух состояний, это надежнее и более устойчиво к различным помехам;
• В-четвертых, есть возможность использования алгебры логики для осуществления логических преобразований;
• В-пятых, двоичная арифметика все же проще десятичной, поэтому является более удобной.
Недостатки двоичной системы счисления
Двоичная система счисления менее удобна, так как человек привык больше пользоваться десятичной системой, которая намного короче. А вот, в двоичной системе большие числа имеет довольно таки большое число разрядов, что и является ее существенным недостатком.
Почему двоичная система счисления так распространена?
Популярной двоичная система счисления является потому, что это язык вычислительной техники, где каждая цифра должна быть каким-то образом представлена на физическом носителе.
Ведь проще иметь два состояния при изготовлении физического элемента, чем придумывать устройство, в котором должно присутствовать десять различных состояний. Согласитесь, что это было бы намного сложней.
По сути, это и есть одной из основных причин популярности двоичной системы счисления.
История возникновения двоичной системы счисления
История создания двоичной системы счисления в арифметике, довольно таки яркая и стремительная. Основателем этой системы считают известного немецкого ученого и математика Г. В. Лейбница. Им была опубликована статья, в которой он описал правила, по которым можно было выполнить всевозможные арифметические операции над двоичными числами.
К сожалению, до начала двадцатого века двоичная система счисления была малозаметна в прикладной математике. А после того, как начали появляться простые счетные механические приборы, то ученые стали более активно обращать внимание на двоичную систему счисления и начали ее активно изучать, так как для вычислительных устройств она была удобна и незаменима. Она является той минимальной системой, с помощью которой можно полностью реализовать принцип позиционности в цифровой форме записи чисел.
Вопросы и задания
1. Назовите преимущества и недостатки двоичной системы счисления по сравнению с десятичной.
2. Какие двоичные числа соответствуют следующим десятичным числам:
128; 256; 512; 1024?
3. Чему в десятичной системе равны следующие двоичные числа:
1000001; 10000001; 100000001; 1000000001?
4. Переведите в десятичную систему следующие двоичные числа:
101; 11101; 101010; 100011; 10110111011.
5. Переведите в двоичную систему счисления следующие десятичные числа:
2; 7; 17; 68; 315; 765; 2047.
6. Выполните сложение в двоичной системе счисления:
11 + 1; 111 + 1; 1111 + 1; 11111 + 1.
7. Выполните умножение в двоичной системе счисления:
111 · 10; 111 · 11; 1101 · 101; 1101 · 1000.
И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс
Отослано читателями из интернет-сайтов
|