|
|
|
| Строка 1: |
Строка 1: |
| - | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика]]>>[[Математика 6 клас|Математика 6 клас]]>> Математика: Тема 1.Розкладання натуральних чисел на прості множники''' | + | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика]]>>[[Математика 6 клас|Математика 6 клас]]>> Математика: Тема 1.Найбільший спільний дільник''' |
| | | | |
| - | <br> | + | <br> <br> |
| | | | |
| | <br>Випишіть усі дільники чисел 18 і 24 і підкресліть їх спільні дільники.<br>число 18 дільники: 2, 3, 6, 9, 18<br>число 24 дільники: І, 2, 3, 4, 6, 8, 12, 24<br>Спільними дільниками (вони підкреслені) чисел 18 і 24 є числа 1, 2, 3, 6, найбільшим з них є 6. Число 6 є найбільшим натуральним числом, на яке діляться і 18, і 24.<br>Найбільше натуральне число, на яке ділиться кожне з даних чисел, називають найбільшим спільним дільником цих чисел.<br>Отже, найбільшим спільним дільником чисел 18 і 24 є число 6. Це скоро¬чено записують так: НСД( 18; 24) = 6.<br>У розглянутому прикладі ми легко знайшли найбільший спільний дільник чисел, записавши всі дільники кожного з них. Якщо числа великі й мають багато дільників, то знаходження найбільшого спільного дільника цим способом є до¬волі громіздким.<br>Розглянемо ще один спосіб знаходження найбільшого спільного дільника, взявши числа 210 і 294. Розкладемо кожне із цих чисел на прості множники:<br>210 = 2 • 3 • 5 • 7; 294 = 2•3•7•7.<br>Підкреслимо всі спільні прості множники в роз¬кладах даних чисел: 2, 3, 7. Числа 210 і 294 діляться на кожне із чисел 2, 3, 7 і на їх добуток: 2•3•7 = 42. Число42 є найбільшим спільним дільником чисел 210 і 294:<br>НСД(210;294) = 42.<br>Назвіть послідовність кроків у знаходженні НСД двох чисел.<br>Для знаходження найбільшого спільного дільника двох чисел можна розкласти ці числа на прості множники і знайти добуток їх спільних множників.<br>За таким правилом можна знаходити найбільший спільний дільник трьох і більше чисел. Знайдемо, наприклад, найбільший спільний дільник чисел 45, 75 і 90. Розкладемо ці числа на прості множники і підкреслимо спільні для усіх чисел множники:<br>45 = 3•3•5; 75 = 3•5•5; 90 = 2•3•3•5.<br>Отже, НСД(45; 75; 90) = 3•5=15.<br>Якщо серед даних чисел є число, на яке діляться інші з даних чисел, то це число є найбільшим спільним дільником даних чисел. Наприклад:<br>НСД(3; 6) = 3; НСД(4; 16; 20) = 4.<br>Два числа, найбільший спільний дільник яких дорівнює 1, називають взаємно простими числами. Наприклад, числа 16 і 27 є взаємно простими, бо їх найбільшим спільним дільником є 1.<br>Взаємно прості числа взагалі мають лише один спільний дільник — число 1. Тому якщо два числа мають спільний дільник, відмінний від 1, то вони не взаєм¬но прості. Наприклад, числа 18 і 45 не є взаємно простими, бо мають спільний дільник 3.<br>Прочитайте<br>1. Яку найбільшу кількість однакових букетів можна скласти із 24 волошок і 32 ромашок, використавши всі квіти?<br>• 3 даних квітів можна, наприклад, скласти 2 букети, у кожному з яких буде 12 волошок і 16 ромашок. Не можна скласти три букети, бо 32 ромашки не можна розділити на 3 однакові частини. Можна скласти чотири однакові букети, бо і 24 волошки, і 32 ромашки можна розділити на 4 однакові частини. Очевидно, що для розв'язання задачі потрібно знайти найбільше число, на яке можна розділити 24 волошки і 32 ромашки, тобто знайти найбільший спільний дільник чисел 24 і 32. Оскільки НСД(24; 32) = 8, то найбільше можна скласти 8 однакових букетів. Кожний такий букет складатиметься із 24 : 8 = 3 волошок і 32 : 8 = 4 ромашок. •<br>Усно<br>124. Чи є число 3 спільним дільником чисел 27 і 45; 57 і 44?<br>125. Знайдіть найбільший спільний дільник чисел:<br>а) 2 і 8; б) 15 ІЗ; в) 15 і 45;<br>г) 15 і 18; Д) 31 і 33; е) 27 і 36.<br>126. Чи є взаємно простими числа 6 і 8; 6 і 9; 6 і 11?<br>127. Серед чисел 2, 9, 15 і 20 вкажіть усі пари взаємно простих чисел.<br>128. Назвіть кілька чисел, взаємно простих із числом 8; не взаємно простих із числом 8.<br>129. Чи може число, взаємно просте із числом 15, ділитися на 3; на 5?<br>130. Чи правильне твердження:<br>а) будь-які два парні числа не є взаємно простими;<br>б) будь-які два прості числа є взаємно простими?<br>Рівень А<br>131. Знайдіть найбільший спільний дільник чисел т і п, якщо: а) т = 2 • 2 • 3 • 5 • 5, п = 2 • 5 • 5 • 7;<br>б)т = 3 • 7 • 7 • 7 • 11, п = 2•7•7•41.<br>Знайдіть найбільший спільний дільник чисел:<br>132. а) 12 і 8; б) 36 і 48; в) 50 і 175; г) 100 і 81;<br>д) 308 і 324; е) 210 і 330; є) 2, 6 і 18; ж) 24, 36 і 42.<br>а) 9 і 12; б) 48 і 72; в) 6 і 78; г) 12 і 35;<br>д) 130 і 78; е) 182 і 156; є) 6, 14 і 36; ж) 32, 64 і 96.<br>134. Знайдіть найбільший спільний дільник чисельника і знаменника дробу:<br>[[Image:Qm6.jpg]] | | <br>Випишіть усі дільники чисел 18 і 24 і підкресліть їх спільні дільники.<br>число 18 дільники: 2, 3, 6, 9, 18<br>число 24 дільники: І, 2, 3, 4, 6, 8, 12, 24<br>Спільними дільниками (вони підкреслені) чисел 18 і 24 є числа 1, 2, 3, 6, найбільшим з них є 6. Число 6 є найбільшим натуральним числом, на яке діляться і 18, і 24.<br>Найбільше натуральне число, на яке ділиться кожне з даних чисел, називають найбільшим спільним дільником цих чисел.<br>Отже, найбільшим спільним дільником чисел 18 і 24 є число 6. Це скоро¬чено записують так: НСД( 18; 24) = 6.<br>У розглянутому прикладі ми легко знайшли найбільший спільний дільник чисел, записавши всі дільники кожного з них. Якщо числа великі й мають багато дільників, то знаходження найбільшого спільного дільника цим способом є до¬волі громіздким.<br>Розглянемо ще один спосіб знаходження найбільшого спільного дільника, взявши числа 210 і 294. Розкладемо кожне із цих чисел на прості множники:<br>210 = 2 • 3 • 5 • 7; 294 = 2•3•7•7.<br>Підкреслимо всі спільні прості множники в роз¬кладах даних чисел: 2, 3, 7. Числа 210 і 294 діляться на кожне із чисел 2, 3, 7 і на їх добуток: 2•3•7 = 42. Число42 є найбільшим спільним дільником чисел 210 і 294:<br>НСД(210;294) = 42.<br>Назвіть послідовність кроків у знаходженні НСД двох чисел.<br>Для знаходження найбільшого спільного дільника двох чисел можна розкласти ці числа на прості множники і знайти добуток їх спільних множників.<br>За таким правилом можна знаходити найбільший спільний дільник трьох і більше чисел. Знайдемо, наприклад, найбільший спільний дільник чисел 45, 75 і 90. Розкладемо ці числа на прості множники і підкреслимо спільні для усіх чисел множники:<br>45 = 3•3•5; 75 = 3•5•5; 90 = 2•3•3•5.<br>Отже, НСД(45; 75; 90) = 3•5=15.<br>Якщо серед даних чисел є число, на яке діляться інші з даних чисел, то це число є найбільшим спільним дільником даних чисел. Наприклад:<br>НСД(3; 6) = 3; НСД(4; 16; 20) = 4.<br>Два числа, найбільший спільний дільник яких дорівнює 1, називають взаємно простими числами. Наприклад, числа 16 і 27 є взаємно простими, бо їх найбільшим спільним дільником є 1.<br>Взаємно прості числа взагалі мають лише один спільний дільник — число 1. Тому якщо два числа мають спільний дільник, відмінний від 1, то вони не взаєм¬но прості. Наприклад, числа 18 і 45 не є взаємно простими, бо мають спільний дільник 3.<br>Прочитайте<br>1. Яку найбільшу кількість однакових букетів можна скласти із 24 волошок і 32 ромашок, використавши всі квіти?<br>• 3 даних квітів можна, наприклад, скласти 2 букети, у кожному з яких буде 12 волошок і 16 ромашок. Не можна скласти три букети, бо 32 ромашки не можна розділити на 3 однакові частини. Можна скласти чотири однакові букети, бо і 24 волошки, і 32 ромашки можна розділити на 4 однакові частини. Очевидно, що для розв'язання задачі потрібно знайти найбільше число, на яке можна розділити 24 волошки і 32 ромашки, тобто знайти найбільший спільний дільник чисел 24 і 32. Оскільки НСД(24; 32) = 8, то найбільше можна скласти 8 однакових букетів. Кожний такий букет складатиметься із 24 : 8 = 3 волошок і 32 : 8 = 4 ромашок. •<br>Усно<br>124. Чи є число 3 спільним дільником чисел 27 і 45; 57 і 44?<br>125. Знайдіть найбільший спільний дільник чисел:<br>а) 2 і 8; б) 15 ІЗ; в) 15 і 45;<br>г) 15 і 18; Д) 31 і 33; е) 27 і 36.<br>126. Чи є взаємно простими числа 6 і 8; 6 і 9; 6 і 11?<br>127. Серед чисел 2, 9, 15 і 20 вкажіть усі пари взаємно простих чисел.<br>128. Назвіть кілька чисел, взаємно простих із числом 8; не взаємно простих із числом 8.<br>129. Чи може число, взаємно просте із числом 15, ділитися на 3; на 5?<br>130. Чи правильне твердження:<br>а) будь-які два парні числа не є взаємно простими;<br>б) будь-які два прості числа є взаємно простими?<br>Рівень А<br>131. Знайдіть найбільший спільний дільник чисел т і п, якщо: а) т = 2 • 2 • 3 • 5 • 5, п = 2 • 5 • 5 • 7;<br>б)т = 3 • 7 • 7 • 7 • 11, п = 2•7•7•41.<br>Знайдіть найбільший спільний дільник чисел:<br>132. а) 12 і 8; б) 36 і 48; в) 50 і 175; г) 100 і 81;<br>д) 308 і 324; е) 210 і 330; є) 2, 6 і 18; ж) 24, 36 і 42.<br>а) 9 і 12; б) 48 і 72; в) 6 і 78; г) 12 і 35;<br>д) 130 і 78; е) 182 і 156; є) 6, 14 і 36; ж) 32, 64 і 96.<br>134. Знайдіть найбільший спільний дільник чисельника і знаменника дробу:<br>[[Image:Qm6.jpg]] |
Версия 12:51, 14 марта 2010
Гіпермаркет Знань>>Математика>>Математика 6 клас>> Математика: Тема 1.Найбільший спільний дільник
Випишіть усі дільники чисел 18 і 24 і підкресліть їх спільні дільники.
число 18 дільники: 2, 3, 6, 9, 18
число 24 дільники: І, 2, 3, 4, 6, 8, 12, 24
Спільними дільниками (вони підкреслені) чисел 18 і 24 є числа 1, 2, 3, 6, найбільшим з них є 6. Число 6 є найбільшим натуральним числом, на яке діляться і 18, і 24.
Найбільше натуральне число, на яке ділиться кожне з даних чисел, називають найбільшим спільним дільником цих чисел.
Отже, найбільшим спільним дільником чисел 18 і 24 є число 6. Це скоро¬чено записують так: НСД( 18; 24) = 6.
У розглянутому прикладі ми легко знайшли найбільший спільний дільник чисел, записавши всі дільники кожного з них. Якщо числа великі й мають багато дільників, то знаходження найбільшого спільного дільника цим способом є до¬волі громіздким.
Розглянемо ще один спосіб знаходження найбільшого спільного дільника, взявши числа 210 і 294. Розкладемо кожне із цих чисел на прості множники:
210 = 2 • 3 • 5 • 7; 294 = 2•3•7•7.
Підкреслимо всі спільні прості множники в роз¬кладах даних чисел: 2, 3, 7. Числа 210 і 294 діляться на кожне із чисел 2, 3, 7 і на їх добуток: 2•3•7 = 42. Число42 є найбільшим спільним дільником чисел 210 і 294:
НСД(210;294) = 42.
Назвіть послідовність кроків у знаходженні НСД двох чисел.
Для знаходження найбільшого спільного дільника двох чисел можна розкласти ці числа на прості множники і знайти добуток їх спільних множників.
За таким правилом можна знаходити найбільший спільний дільник трьох і більше чисел. Знайдемо, наприклад, найбільший спільний дільник чисел 45, 75 і 90. Розкладемо ці числа на прості множники і підкреслимо спільні для усіх чисел множники:
45 = 3•3•5; 75 = 3•5•5; 90 = 2•3•3•5.
Отже, НСД(45; 75; 90) = 3•5=15.
Якщо серед даних чисел є число, на яке діляться інші з даних чисел, то це число є найбільшим спільним дільником даних чисел. Наприклад:
НСД(3; 6) = 3; НСД(4; 16; 20) = 4.
Два числа, найбільший спільний дільник яких дорівнює 1, називають взаємно простими числами. Наприклад, числа 16 і 27 є взаємно простими, бо їх найбільшим спільним дільником є 1.
Взаємно прості числа взагалі мають лише один спільний дільник — число 1. Тому якщо два числа мають спільний дільник, відмінний від 1, то вони не взаєм¬но прості. Наприклад, числа 18 і 45 не є взаємно простими, бо мають спільний дільник 3.
Прочитайте
1. Яку найбільшу кількість однакових букетів можна скласти із 24 волошок і 32 ромашок, використавши всі квіти?
• 3 даних квітів можна, наприклад, скласти 2 букети, у кожному з яких буде 12 волошок і 16 ромашок. Не можна скласти три букети, бо 32 ромашки не можна розділити на 3 однакові частини. Можна скласти чотири однакові букети, бо і 24 волошки, і 32 ромашки можна розділити на 4 однакові частини. Очевидно, що для розв'язання задачі потрібно знайти найбільше число, на яке можна розділити 24 волошки і 32 ромашки, тобто знайти найбільший спільний дільник чисел 24 і 32. Оскільки НСД(24; 32) = 8, то найбільше можна скласти 8 однакових букетів. Кожний такий букет складатиметься із 24 : 8 = 3 волошок і 32 : 8 = 4 ромашок. •
Усно
124. Чи є число 3 спільним дільником чисел 27 і 45; 57 і 44?
125. Знайдіть найбільший спільний дільник чисел:
а) 2 і 8; б) 15 ІЗ; в) 15 і 45;
г) 15 і 18; Д) 31 і 33; е) 27 і 36.
126. Чи є взаємно простими числа 6 і 8; 6 і 9; 6 і 11?
127. Серед чисел 2, 9, 15 і 20 вкажіть усі пари взаємно простих чисел.
128. Назвіть кілька чисел, взаємно простих із числом 8; не взаємно простих із числом 8.
129. Чи може число, взаємно просте із числом 15, ділитися на 3; на 5?
130. Чи правильне твердження:
а) будь-які два парні числа не є взаємно простими;
б) будь-які два прості числа є взаємно простими?
Рівень А
131. Знайдіть найбільший спільний дільник чисел т і п, якщо: а) т = 2 • 2 • 3 • 5 • 5, п = 2 • 5 • 5 • 7;
б)т = 3 • 7 • 7 • 7 • 11, п = 2•7•7•41.
Знайдіть найбільший спільний дільник чисел:
132. а) 12 і 8; б) 36 і 48; в) 50 і 175; г) 100 і 81;
д) 308 і 324; е) 210 і 330; є) 2, 6 і 18; ж) 24, 36 і 42.
а) 9 і 12; б) 48 і 72; в) 6 і 78; г) 12 і 35;
д) 130 і 78; е) 182 і 156; є) 6, 14 і 36; ж) 32, 64 і 96.
134. Знайдіть найбільший спільний дільник чисельника і знаменника дробу:

Чи є взаємно простими числа:
135. а) 3 і 1000; б) 49 і 240; в) 154 і 165; г) 14 332 і 8156?
136.
а) 7 і 4000; б) 36 і 245; в) 187 і 230; г) 40 302 і 8001?
137. Запишіть усі числа, менші за 12 і взаємно прості із числом 12.
138.
Запишіть усі правильні дроби зі знаменником 8, у яких чисельник і зна¬менник є взаємно простими числами.
139. Запишіть усі неправильні дроби із чисельником 6, у яких чисельник і знаменник є взаємно простими числами.
Рівень Б
140. Знайдіть хоча б три значення а, за яких найбільшим спільним дільником чисел 18 і а є число 6.
141. Яку найбільшу кількість однакових подарунків можна скласти із 48 цукерок і 36 яблук, якщо використати всі цукерки й усі яблука?
142.
Прямокутний аркуш паперу завдовжки 56 см і завширшки 48 см потрібно розрізати без відходів на найменшу кількість рівних квадратів. Скільки квадратів одержимо?
143. Дерев'яний брусок завдовжки 48 см, завширшки 30 см і заввишки 24 см потрібно розрізати без відходів на найменшу кількість рівних кубів. Скільки кубів одержимо?
144
Яку найбільшу кількість однакових подарунків можна скласти з 90 мандаринів, 405 цукерок і 135 пряників, якщо потрібно використати всі мандарини, цукерки і пряники?
145. Між усіма учнями класу розділили порівну 58 зошитів у лінійку і 87 зошитів у клітинку. Скільки учнів у класі? Скільки зошитів у лінійку і скільки у клітинку отримав кожен учень?
146. У кімнаті завдовжки 625 см і завширшки 475 см вирішили викласти долів¬ку однаковими декоративними плитками квадратної форми, не розрізуючи їх. Який найбільший можливий розмір такої плитки? Скільки плиток най¬більшого розміру потрібно, щоб викласти ними долівку?
Здогадайтеся
147. У змаганнях беруть участь 90 учнів. На футболці кожного з учасників нанесено номер від 10 до 99 включно. Фірма «Пінг-Понг» вручила призи власникам тих номерів, які діляться на кожну із цифр у запису номера. Скільки учнів одержали призи?
Вправи для повторення
148. Шлях завдовжки 210 км автомобіль проїхав в одному напрямі за 3 год, а у зворотному — за 4 год. Яка середня швидкість автомобіля за весь час руху?
149. За 3 год мотоцикліст проїхав 135 км, до того ж за першу годину він про¬їхав на 2 км більше, ніж за другу. Протягом третьої години мотоцикліст рухався зі швидкістю, яка дорівнює середній швидкості його руху за ці З год. Скільки кілометрів проїхав мотоцикліст за кожну годину?
150. Агроном підрахував, що із 32 га поля зібрали 352 т картоплі, а з решти 18 га — 207 т. Скільки картоплі зібрали в середньому з 1 га поля?
151. Розмістіть у порядку зростання числа: 11 1/4 11,3; 11 1/5; 11,23.
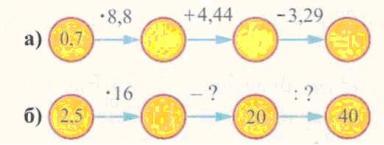
152. Знайдіть пропущені числа.
Онлайн-бібліотека з підручниками і книгами, тести з математики, завдання з математики 6 клас, календарне планування
Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту
 конспект уроку і опорний каркас конспект уроку і опорний каркас
 презентація уроку презентація уроку
 акселеративні методи та інтерактивні технології акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями) закриті вправи (тільки для використання вчителями)
 оцінювання
Практика оцінювання
Практика
 задачі та вправи,самоперевірка задачі та вправи,самоперевірка
 практикуми, лабораторні, кейси практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання
Ілюстрації домашнє завдання
Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати реферати
 фішки для допитливих фішки для допитливих
 шпаргалки шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення
 зовнішнє незалежне тестування (ЗНТ) зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні підручники основні і допоміжні
 тематичні свята, девізи тематичні свята, девізи
 статті статті
 національні особливості національні особливості
 словник термінів словник термінів
 інше
Тільки для вчителів інше
Тільки для вчителів
 ідеальні уроки ідеальні уроки
 календарний план на рік календарний план на рік
 методичні рекомендації методичні рекомендації
 програми програми
 обговорення обговорення
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












