Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Существование треугольника, равного данному. Полные уроки

ТЕМА УРОКА: Существование треугольника, равного данному.

Цели урока:

• Образовательные – повторение, обобщение и проверка знаний по теме: “Существование треугольника, равного данному”; выработка основных навыков.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные - посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока:

• Формировать навыки в построении треугольников с помощью масштабной линейки, транспортира и чертежного треугольника.
• Проверить умение учащихся решать задачи.

План урока:

1. Повторение.
   
2. Интересное для учеников.
   
3. Существование треугольника, равного данному
   
4. Задание для самостоятельной проверки.

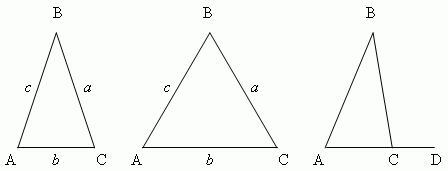
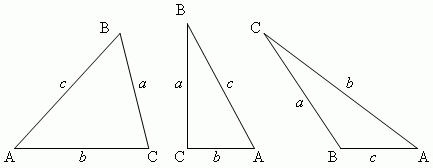
Повторение

Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.
Трём точкам пространства, не лежащим на одной прямой, соответствует одна и только одна плоскость.
Любой многоугольник можно разбить на треугольники — этот процесс называется триангуляция.
Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.

Типы треугольников:
Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:

• Если все углы треугольника острые, то треугольник называется остроугольным;
• Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
• Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
  

По числу равных сторон:

• Разносторонним называется треугольник, у которого длины трёх сторон попарно различны.
• Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
• Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.

Это интересно

В любом треугольнике:

1. Против большей стороны лежит больший угол, и наоборот.
   
2. Против равных сторон лежат равные углы, и наоборот.
   
3. Сумма углов треугольника равна 180 ?
   
4. Продолжая одну из сторон треугольника, получаем внешний угол. Внешний угол треугольника равен сумме внутренних углов, не смежных с ним.
   
5. Любая сторона треугольника меньше суммы двух других сторон и больше их разности ( a < b + c, a > b – c; b < a + c, b > a – c; c < a + b, c > a – b ).
   

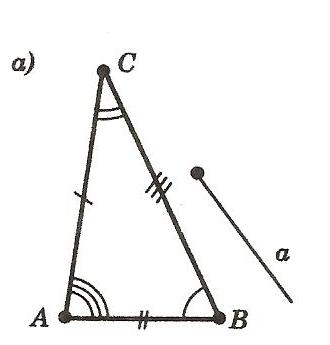
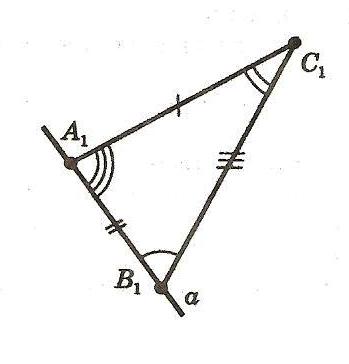
Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.

На рисунке изображен треугольник ABC и луч "a".  Переместим треугольник ABC так, чтобы его вершина A совместилась с началом луча "a", вершина B попала на луч "a", а вершина C оказалась в заданной полуплоскости относительно луча "a" и его продолжения.

Вершины нашего треугольника в этом новом положении обозначим A₁, B₁, C₁. Треугольник A₁, B₁, C₁ равен треугольнику ABC.

Существование треугольника A₁, B₁, C₁, равного треугольнику ABC и расположенного указанным образом относительно заданного луча a, мы относим к числу основных свойств простейших фигур.

Сформулируем это свойство так:

Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Существование треугольника, равного данному.

Два треугольника называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие стороны должны лежать против соответствующих углов.
Существование треугольника, равного данному, мы относим к числу аксиом. (Казалось бы, что это очевидно, но ведь доказать нельзя!)

Справка

Аксиома - утверждения, содержащиеся в формулировках основных свойств простейших фигур не доказываются и называются аксиомами. Слово «аксиома» греческого происхождения и означает «утверждение, не вызывающее сомнений».

При доказательстве теорем разрешается пользоваться основными свойствами простейших фигур (аксиомами), а также свойствами, уже доказанными теоремами. Никакими другими свойствами пользоваться нельзя, даже если они кажутся очевидными.

При доказательстве теорем разрешается пользоваться чертежом как геометрической записью того, что выражено словами. Не разрешается использовать в рассуждении свойства фигуры, видные на чертеже, если их невозможно обосновать опираясь на аксиомы и теоремы раннее доказанные.

Каков бы ни был треугольник, существует равный ему треугольник.

При доказательстве равенства треугольников, необходимо доказывать, что все шесть пар соответствующих элементов равны. Следующие три теоремы дадут нам признаки равенства треугольников по трем парам элементов.

(I признак равенства треугольников):  Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

(II признак равенства треугольников): Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

(III признак равенства треугольников): Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Параллельные прямые и связанные с ними углы.

Внутренние накрест лежащие углы, образованные при пересечении двух прямых  третьей, равны тогда и только тогда, когда прямые параллельны.
Нам понадобятся  некоторые свойства параллельных прямых для того, чтобы доказать  теоремы об углах треугольника.

• Две прямые параллельны, если они не пересекаются и лежат в одной плоскости.
• Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
• Секущей называется прямая, пересекающая две другие прямые, лежащие в одной плоскости.

Основное свойство параллельных прямых:

• Через точку, не лежащую на данной прямой можно провести параллельную ей прямую и притом только одну.
• Две прямые, расположенные в одной плоскости, параллельны тогда и только тогда, когда соответственные углы, образованные секущей, равны.
• Две прямые, расположенные в одной плоскости, параллельны тогда и только тогда, когда внутренние накрест лежащие углы, образованные секущей, равны.
• Две прямые, расположенные в одной плоскости, параллельны тогда и только тогда, когда сумма внутренних односторонних углов, образованных секущей, равна 180».

Заметьте, что теоремы содержат выражение "если и только если". То есть два утверждения типа "если /то" содержатся в одном. В этом случае они называются необходимым и достаточным условиями.

Справка.

НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ - в математике.

Необходимыми условиями правильности утверждения "А" называются такие условия, без соблюдения которых утверждение "А" не может быть верным.

Достаточными - условия, при выполнении которых утверждение "А" верно.

Поэтому для доказательств этих теорем требуется доказать по два утверждения для каждой.

Следующие утверждения есть следствие теорем о параллельных прямых.

• Две прямые, перпендикулярные третьей, параллельны.
  
• Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
  
• Сумма внутренних углов треугольника равна 180».
  

Интересный факт:

Треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.

Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух, расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси. Имеет применение в теории вероятности и обладает занимательными свойствами.

"Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике."

Мартин Гарднер

Исторический факт.

Первое упоминание треугольной последовательности биномиальных коэффициентов под названием meru-prastaara встречается в комментарии индийского математика X века Халаюдхи к трудам другого математика, Пингалы. Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма. В 1303 году была выпущена книга «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе, в которой был изображен треугольник Паскаля на одной из иллюстраций; считается, что изобрёл его другой китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя). На титульном листе учебника арифметики, написанном в 1529 году Петром Апианом, астрономом из Ингольтштадского университета, также изображён треугольник Паскаля. А в 1653 году (в других источниках в 1655 году) вышла книга Блеза Паскаля «Трактат об арифметическом треугольнике».

Файл:29012011 5.gifТреугольник Яна Хуэя в китайском средневековом манускрипте, 1303 год

Вопросы:

1. Что такое теорема?
   
2. Что такое необходимые и достаточные условия?
3. Признаки равенства треугольника?
   

Список использованных источников:

1. Федеральный общеобразовательный стандарт. Вестник образования. №12,2004.
2. Программы общеобразовательных учреждений. Геометрия 7-9 классы. Составитель: С.А. Бурмистрова. Москва. «Просвещение», 2009 год.
3. Руководитель НОУ: Рябова Елена Александровна 2008 г.
4. Урок на тему "Треугольник" Автор: Макаренко К.Э., г. Киев

Отредактировано и выслано Потурнаком С. А.

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.