|
Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Определение декартовых координат. Полные уроки ТЕМА УРОКА: Определение декартовых координат.
Цели урока:
|

| 
|
| Рене Декарт | Флаг Турени |
Рене Декарт родился 31 марта 1596 года в маленьком городке Ла-Гэ в Турени.
Турень — бывшая провинция Франции. Столицей был город Тур. Во время политической реорганизации территории Франции в 1790 году, территория Турени была разделена между департаментами Эндр и Луара (Indre-et-Loire), Луар и Шер (Loir-et-Cher) и Эндр (Indre).
Род Декартов принадлежал к незнатному чиновному дворянству. Его мать, разрешившись от бремени, через несколько дней умерла. Рене остался жив, но до двадцати лет короткий, сухой кашель и бледный цвет лица внушали опасения за его жизнь. Детство Рене провел в Турени, славившейся садами, плодородием и мягкостью климата. В 1612 году Декарт закончил школу. Он провел в ней восемь с половиной лет.
Начальное образованиеДекарт получил в иезуитском коллеже Ла Флеш, где познакомился с Мареном Мерсенном (тогда — учеником, позже — священником), будущим координатором научной жизни Франции. Религиозное образование, как ни странно, только укрепило в молодом Декарте скептическое недоверие к тогдашним философским авторитетам. Позже он сформулировал свой метод познания: дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.
В 1612 году Декарт закончил коллеж, некоторое время изучал право в Пуатье, затем уехал в Париж, где несколько лет чередовал рассеянную жизнь с математическими исследованиями. Затем он поступил на военную службу (1617) — сначала в революционную Голландию (в те годы — союзника Франции), затем в Германию, где участвовал в недолгой битве за Прагу (Тридцатилетняя война). Несколько лет Декарт провёл в Париже, предаваясь научной работе. Помимо прочего, он открыл принцип виртуальных скоростей, который в то время никто ещё не был готов оценить по достоинству.
Затем — ещё несколько лет участия в войне (осада Ларошели). По возвращении во Францию оказалось, что свободомыслие Декарта стало известно иезуитам, и те обвинили его в ереси. Поэтому Декарт переезжает в Голландию (1628), где провёл 20 лет. Наконец, в 1634 году он закончил свою первую, программную книгу под названием "Мир" (Le Monde) из двух частей: "Трактат о свете" и "Трактат о человеке".
Спустя некоторое время, однако, одна за другой, появляются другие книги Декарта:
- "Рассуждение о методе..." (1637)
- "Размышления о первой философии..." (1641)
- "Начала философии" (1644)
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе"Рассуждение о методе" в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
Декартова система координат.
И так эта система координат имеет два своих вполне оправданных названия. Первым из них является декартова, такое название она получила от фамилии своего автора. И второе не менее интересное и оправданное - прямоугольная система координат, происхождение такого имени становится понятным после первого взгляда на саму систему координат. Угол между двумя направляющими равен 90° такое угол зачастую называют прямым, откуда и пошло второе название.
Горизонтальная ось называется осью ОХ, вертикальная — осью OY. Место пересечения осей ОХ и OY называется началом координат, которое также обозначают цифрой 0 (“ноль”). Каждая точка на координатной плоскости имеет свой точный адрес. Это пара чисел: первое число по оси ОХ, второе — по оси OY. Эти числа называются координатами точки. А чтобы не путать порядок следования координат, вспомните, как устроены наши дома: сначала мы заходим в нужный подъезд (по оси ОХ), а затем поднимаемся на нужный этаж (по оси ОУ).
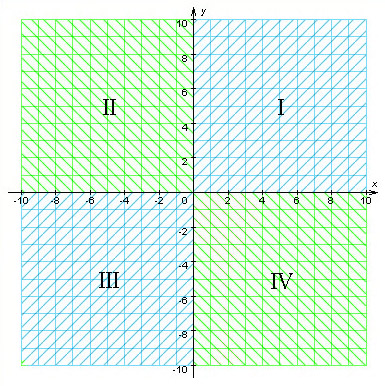
Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями.
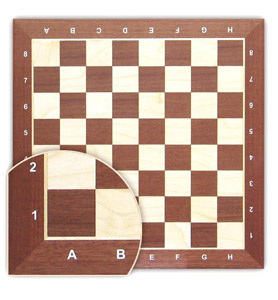
Посмотрите на шахматную доску. Вдоль её нижнего края идет ряд букв, а вдоль левого — ряд цифр. С их помощью можно однозначно определять положение любой фигуры на шахматной доске.
Пример.
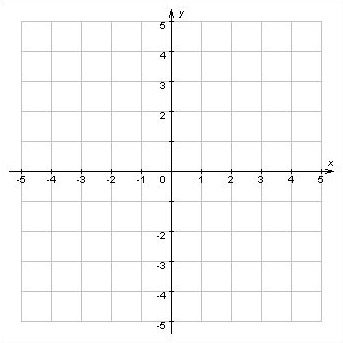
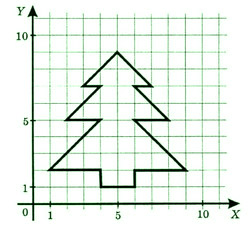
Известны координаты пятнадцати точек: А(4, 1), Б(4, 2), В(1, 2), Г(4, 5), Д(2, 5), Е(4, 7), Ж(3, 7), З(5, 9), И(7, 7), К(6, 7), Л(8, 5), М(6, 5), Н(9, 2), О(6, 2), П(6, 1). Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности А—Б—В—Г—Д—Е—Ж—З—И—К—Л—М —Н—О—П—А, то получим следующий рисунок:
Применение на практике.
Разобравшись что все предметы должны иметь свое место можно сказать прямоугольная система координат отыграла важную роль в развитии теоретических так и прикладных наук. Одно из центральных мест занимающих в прикладных науках это бесспорно строительство, с ростом потребностей людей выделить свои дома среди других. Быть уникальными и неповторимыми человеку приходилось все время усовершенствовать свои навыки. С развитием технологий некоторые задачи люди смогли поручить машинам, но как и прежде без человеческого управления ничего не получится. Даже самые сложные и совершенные компьютерные программы такие как AUTOCAD используют такую простую и не заумную систему координат.
Все фигуры (или "примитивы", как их ещё называют) в AutoCAD состоят из точек. Отрезок имеет две точки; прямоугольник – четыре; у круга, дуги, эллипса есть центр и так далее. Эти точки мы можем "ставить" произвольно в любом месте Рабочего пространства – щелчком левой кнопки мыши, а можем точно вводить координаты каждой точки.
Ввод координат точек обеспечивает точность построений.
В AutoCAD координаты можно вводить в двух системах координат: декартовой (вводятся координаты Х, Y) и полярной (первая координата – длина отрезка, вторая – угол к оси Х).
На следующих видео можно увидеть как выглядит проектирование деталей и остальных частей в мощных программных пакетах.
Интересный факт:
Навигационные устройства.
Сегодня мы затронули очень интересную тему о навигации, хотелось бы подробней углубится как же все это работает.
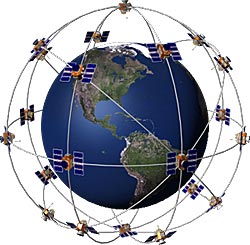
Спутниковые системы определения координат (российская Глонасс и американская GPS), в состав которых входят:комплекс наземных станций автоматического наблюдения за спутниками, искусственные спутники Земли с радиусом орбит около 26 000 км и приемная аппаратура потребителей.
При функционировании системы пространственное положение спутников определяют с наземных станций наблюдений, равномерно расположенных по всему миру и имеющих определенные пространственные координаты. Все станции связаны с головной станцией управления высокоскоростными линиями передачи данных и уточнения параметров орбит спутников в единой системе координат.
Спутники передают периодически уточняемые эфемириды - набор координат, которые определяют положение спутников на орбите в различные моменты времени. Под влиянием гравитационного поля Земли и других факторов параметры исходных координат спутниковых систем изменяются и поэтому постоянно уточняются. В настоящее время точность "бортовых эфемирид", которые получают путем экстраполяции уточненной орбиты на несколько дней вперед, составляет 20-100 м, а при использовании специальных методов обработки - около 1 м.
При эксплуатации системы GPS определение местоположения предусмотрено в Мировой системе координат 1984 г (WGS-84). Начало координат в этой системе находится в центре масс Земли, ось Z параллельна направлению на условный земной полюс, ось X определяется плоскостями начального меридиана WGS-84 и экватора. Начальный меридиан WGS-84 параллелен нулевому меридиану, закрепленному координатами станций наблюдений. Ось Y дополняет систему координат до правой. Начало и положение осей координат системы WGS-84 совпадают с геометрическим центром и осями общеземного эллипсоида WGS-84.
В России создана геодезическая система координат ПЗ-90 (параметры Земли 1990 г). Она закрепляется 30 опорными пунктами на территории бывшего СССР, координаты которых получены методами космической геодезии.
С развитием технологий люди смогли превратить все это в сверх полезные вещи для себя одним из таких примеров является GPS навигатор.
Вопросы:
- Кто такое Декарт и чем он известен?
- В чем разница между декартовой и прямоугольной системами координат ?
- Зачем нужны системы координат?
Список использованных источников:
- Изотова Татьяна Григорьевна, учитель информатики.
- Кузнецов Б. Г. Эволюция картины мира.
- В. И. Гервидс Модель декартовой системы координат.
Над уроком работали:
Потурнак С.А.
Изотова Татьяна Григорьевна
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: