Гипермаркет знаний>>Информатика >>Информатика 7 класс>> Управление исполнителем Робот

                                                          § 3.3. Управление исполнителем Робот

                                                                          Знакомимся с Роботом

Исполнитель Робот действует на прямоугольном клетчатом поле. Между некоторыми клетками поля могут быть расположены стены. Некоторые клетки могут быть закрашены (рис. 3.11).


 
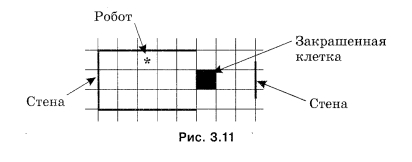
Робот занимает ровно одну клетку поля. По командам вверх, вниз, влево и вправо Робот перемещается в соседнюю клетку в указанном направлении. Если на пути оказывается стена, то происходит отказ — выдается сообщение о невозможности выполнить очередную команду.

По команде закрасить Робот закрашивает клетку, в которой .стоит. Если клетка уже была закрашена, то она закрасится повторно, хотя никаких видимых изменении не произойдет.

Важно помнить, что Робот может исполнять только правильно записанные команды. Например, если вместо команды вниз написать внис, то Робот эту запись не поймет и сразу же сообщит об ошибке.

Вспомните, как называются ошибки в записи команд. Каких еще ошибок следует избегать при разработке алгоритмов?

                                                                Пример алгоритма управления Роботом

Напишем программу, исполняя которую Робот нарисует на клетчатом поле меандр из пяти витков (рис. 3.12).
 


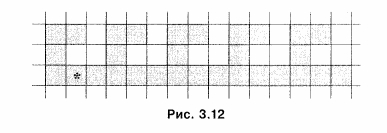
Программа может иметь вид:

ПОВТОРИТЬ 5 РАЗ
 вправо
 закрась; влево
 закрась; влево
 закрась; вверх
 закрась; вверх
 закрась; вправо; закрась
 вправо; вправо; вправо
 вниз; вниз
КОНЕЦ

Здесь мы использовали конструкцию повторения, так как совершенно одинаковые фрагменты повторяются на рисунке 5 раз. При записи тела цикла мы в одной строке через точку с запятой записывали несколько команд.

Если оформить процедуру виток, то основная программа окажется совсем короткой.

Вспомогательный алгоритм:
ПРОЦ виток
НАЧАЛО
вправо
закрась; влево
закрась; влево
закрась; вверх
закрась; вверх
закрась; вправо; закрась
вправо; вправо; вправо
вниз; вниз
КОНЕЦ

Основной алгоритм:
ПОВТОРИТЬ 5 РАЗ
 виток
КОНЕЦ

Предложите свой вариант программы для рисования меандра.

                                                                            Цикл «пока»
 
А теперь попробуем написать программу для решения очень простой задачи: закрасить все клетки справа от Робота (рис. 3.13).

 
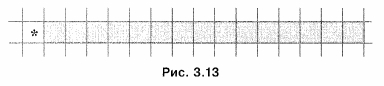
Правда, сколько именно клеток следует закрасить, не уточнено. Известно только, что:

1) справа на неизвестном расстоянии есть стена;
2) клетки нужно красить, пока Робот не подойдет к стене вплотную.

Воспользуемся тем, что Робот может анализировать и сообщать обстановку вокруг себя, проверяя следующие простые условия:

справа свободно
слева свободно
сверху свободно
снизу свободно
закрашено

Ясно, что пока будет выполняться условие справа свободно, нужно выполнять команды:

вправо
закрась

Для оформления таких последовательностей действий используется специальная конструкция алгоритмического языка — цикл «пока».

ПОКА справа свободно ДЕЛАТЬ
 вправо
 закрась
КОНЕЦ
 
В общем виде цикл «пока» записывается так:

ПОКА <условие> ДЕЛАТЬ
 <тело цикла (последовательность команд)>
КОНЕЦ

Блок-схема цикла «пока» имеет вид, показанный на рис. 3.14.

 
Рис. 3.14

При выполнении этого цикла исполнитель повторяет следующие действия:

1) проверяет записанное после служебного слова ПОКА условие;

2) если условие не соблюдается (Робот ответил «Нет»), то выполнение цикла прекращается, и Робот начинает выполнять команды, записанные после служебного слова КОНЕЦ. Если же условие соблюдается (Робот ответил «Да»), то Робот выполняет тело цикла и снова проверяет условие. 

Напишем программу, исполняя которую Робот нарисует на клетчатом поле меандр (рис. 3.12), число витков которого зависит от положения правой стены.

Виток меандра умещается на клетчатом поле, если между клеткой, занимаемой Роботом, и правой стеной есть 1 клетка.

ПОКА справа свободно ДЕЛАТЬ
 вправо
 закрась; влево
 закрась; влево
 закрась; вверх
 закрась; вверх
 закрась вправо; закрась
 вправо; вправо; вправо
 вниз; вниз
КОНЕЦ

В зависимости от исходного положения Робота тело цикла пока может не выполниться ни разу. Такая ситуация не является отказом.

Подумайте, каким должно быть исходное положение Робота в программе рисования меандра, чтобы тело цикла не выполнилось ни разу.

Из-за логических ошибок, допущенных при составлении алгоритма, может возникнуть ситуация зацикливания. Это значит, что условие будет всегда соблюдаться, и выполнение цикла «пока» никогда не завершится.

Рассмотрим следующий пример:
 
ПОКА справа свободно ДЕЛАТЬ
     вправо; влево
КОНЕЦ

Что будет происходить, если справа от Робота нет стены?

Условие в цикле «пока» проверяется только перед вы полнением тела цикла, но не в процессе его выполнения. 

Подумайте, что произойдет, если Робот начнет выполнять нашу программу рисования меандра с циклом «пока», находясь в следующем исходном положении:

карт

Что общего у циклов «повторить п раз» и «пока»? Какие между ними отличия? Нужны ли две конструкции для описания повторяющихся действий?

                                                                              Простые и составные условия

В цикле «пока» могут использоваться не только простые, но и составные условия.

Составное условие образуется из одного или нескольких простых условий и служебных слов И, ИЛИ, НЕ.

Рассмотрим составное условие А И В, где А, В — простые условия. Условие А И В выполнено, когда выполнено каждое из двух входящих в него простых условий.

Пусть А - простое условие справа свободно, В — простое условие справа свободно. Рассмотрим подробно проверку составного условия А И В - сверху свободно.  (рис. 3.15).

карт

В случае а выполнено условие А (сверху свободно), выполнено условие В (справа свободно). Составное условие А И В(сверху свободно И справа свободно)также выполнено.

В случае б выполнено условие А, условие В не выполнено. Составное условие А И В не выполнено.

В случае в не выполнено условие А, условие В выполнено. Составное условие А И В не выполнено.

В случае г не выполнено условие А, не выполнено условие В. Составное условие А И В не выполнено.

Нужно ли проверять условие В в составном условии АИВ, если условие А не выполнено?

Составное условие А ИЛИ В выполнено, когда выполнено хотя бы одно из двух входящих в него простых условий.

Рассмотрим проверку составного условия А ИЛИ В — сверху свободно ИЛИ справа свободно (см. рис. 3.15).

В случае а выполнено условие А (сверху свободно), выполнено условие В (справа свободно). Составное условие А ИЛИ В (сверху свободно ИЛИ справа свободно) выполнено.

В случае б выполнено условие А, не выполнено условие В. Составное условие А ИЛИ В выполнено.

В случае в не выполнено условие А, выполнено условие В. Составное условие А ИЛИ В выполнено.

В случае г не выполнено условие А, не выполнено условие В. Составное условие А ИЛИ в не выполнено.

Нужно ли проверять условие В в составном условии А ИЛИ В, если условие А выполнено?

Составное условие НЕ А выполнено, когда не выполнено условие А.

Пусть А — простое условие закрашено. Рассмотрим проверку составного условия НЕ А (рис. 3.16).
            
карт

В случае а условие А выполнено, условие НЕ А (НЕ закрашено) не выполнено.

В случае б условие А не выполнено, условие НЕ А (НЕ закрашено) выполнено. 

Рассмотрим пример использования составного условия.

Известно, что Робот находится где-то в вертикальном коридоре. Ни одна из клеток коридора не закрашена.

Составим алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернется в исходное положение.

Так как Роботу предстоит закрасить только клетки коридора, мы должны «научить» его их распознавать. Чем же клетки коридора отличаются от всех прочих клеток поля? Из рис. 3.17 видно, что каждая клетка коридора слева и справа ограничена стеной.

карт
 
Робот находится в коридоре, пока слева стена и справа стена. В СКИ нашего исполнителя такие условия не предусмотрены. Там есть противоположные условия: слева свободно, справа свободно. Используем служебное слово НЕ:

слева стена —> НЕ слева свободно
справа стена —> НЕ справа свободно

Нужное условие примет вид:
НЕ слева свободно И НЕ справа свободно.

Представим план действий Робота укрупненными шагами (рис. 3.18).
 
карт
 
Для простоты предположим, что над коридором и под коридором есть хотя бы по одной клетке без стен (иначе придется делать дополнительные проверки сверху свободно, снизу свободно).

1. Чтобы закрасить все клетки коридора, находящиеся выше Робота, прикажем Роботу шагнуть вверх и выполним цикл «пока»:

вверх
ПОКА НЕ слева свободно И НЕ справа свободно ДЕЛАТЬ
  закрась
  вверх
КОНЕЦ

Под управлением этого алгоритма Робот закрасит все клетки коридора, находящиеся выше от него, и окажется на клетке рядом с верхней границей коридора.

При каком исходном положении Робота этот цикл не выполнится ни разу?

2. Командой вниз вернем Робота в коридор. Наша задача — вернуть его в исходную точку. Эта точка имеет единственный отличительный признак — она не закрашена. Поэтому пока занимаемая Роботом клетка оказывается закрашенной, будем перемещать его вниз:

вниз
ПОКА закрашено ДЕЛАТЬ
  вниз
КОНЕЦ

Под управлением этого алгоритма Робот окажется в исходной клетке.

3. Выполнив команду вниз, Робот пройдет исходную клетку и займет первую клетку, расположенную ниже исходной. Теперь можно закрашивать клетки коридора, расположенные ниже исходной:

вниз
ПОКА НЕ слева свободно И НЕ справа свободно
ДЕЛАТЬ
 закрась
 вниз
КОНЕЦ

Возможна ли ситуация, что этот цикл не выполнится ни разу?

4. Так как, выполнив предыдущий алгоритм, Робот окажется под коридором, командой вверх вернем его в коридор. Возвращение в исходную точку обеспечивается алгоритмом:

вверх
ПОКА закрашено ДЕЛАТЬ
 вверх
КОНЕЦ

5. По команде закрась Робот закрашивает исходную точку.

Полностью программа управления Роботом выглядит так:

вверх
ПОКА НЕ слева свободно И НЕ справа свободно
ДЕЛАТЬ
  закрась
  вверх
КОНЕЦ
вниз
ПОКА закрашено ДЕЛАТЬ
  вниз
КОНЕЦ
вниз
ПОКА НЕ слева свободно И НЕ справа свободно
ДЕЛАТЬ
  закрась
  вниз
КОНЕЦ
вверх
ПОКА закрашено ДЕЛАТЬ
  вверх
КОНЕЦ
закрась
 
                                                                                     Команда ветвления

Вспомним, что форма организации действий, при которой в зависимости от выполнения или невыполнения некоторого условия совершается либо одна, либо другая последовательность действий, называется ветвлением.

Графически ветвление можно представить, как показано на рис. 3.19.
 
карт

Для организации ветвлений в СКИ Робота предусмотрена специальная команда ЕСЛИ. Ее общий вид:

ЕСЛИ <условие> ТО <серия действий 1>
ИНАЧЕ <серия действий 2>
КОНЕЦ

Служебные слова ЕСЛИ, ТО, ИНАЧЕ имеют обычный смысл.

Между ТО и ИНАЧЕ записываются одно или несколько действий, составляющих серию действий 1. Между ИНАЧЕ и КОНЕЦ помещается серия действий 2. Служебное слово ИНАЧЕ вместе с серией действий 2 может отсутствовать (сокращенная форма ветвления).

Пусть теперь Робот находится в горизонтальном коридоре, нижняя граница которого сплошная, а в верхней имеются выходы (рис. 3.20). Требуется провести Робота через весь коридор и закрасить клетки коридора, не имеющие верхних границ.

карт

Единственным признаком коридора является наличие нижнеи границы, т. е. выполнение условия НЕ снизу свободно. Если при этом выполняется условие сверху свободно, то клетку нужно закрасить, иначе — красить не надо. Аналогично случаю закрашивания вертикального коридора, предполагаем, что слева и справа от горизонтального коридора есть клетки. Блок-схема алгоритма имеет вид, показанный на рис. 3.21.
 
Рис. 3.21
 
Программа:

ПОКА НЕ снизу свободно ДЕЛАТЬ
  ЕСЛИ сверху свободно ТО
    закрась
  КОНЕЦ
  вправо
КОНЕЦ

Коротко о главном

Исполнитель Робот действует на прямоугольном клетчатом поле. Между некоторыми клетками поля могут быть расположены стены. Некоторые клетки могут быть закрашены. Робот занимает ровно одну клетку поля.

Система команд исполнителя представлена в следующей таблице:

Робот может выполнять цикл «повторить n раз».

Если заранее не известно, сколько именно раз следует выполнить тело цикла, используется специальная конструкция алгоритмического языка — цикл «пока».

В цикле «пока» могут использоваться не только простые, но и составные условия. Составное условие образуется из одного или нескольких простых условий и служебных слов И, ИЛИ, НЕ.

Для организации ветвлений в СКИ Робота предусмотрена специальная команда ЕСЛИ.

Вопросы и задания

1. Приведите все алгоритмы из трех команд, которые переместят Робота из исходного положения в клетку Б.

карт

Существует ли для этой задачи алгоритм, при выполнении которого Робот делает: а) два шага; б) четыре шага; в) пять шагов; г) семь шагов; д) 2001 шаг; е) 2006 шагов?

2. Петя составил алгоритм, переводящий Робота из клетки А в клетку Б с закрашиванием каких-то клеток. Что должен сделать Коля с этим алгоритмом, чтобы получить алгоритм, переводящий Робота из Б в А и закрашивающий те же клетки?

3. Петя составил алгоритм, при выполнении которого Робот вернулся в исходное положение. Коля стер одну из команд. При выполнении Колиного алгоритма Робот также вернулся в исходное положение. Какую команду стер Коля?

4. Маша придумала узор для Робота. Коля стер ровно половину закрашенных клеток. Восстановите рисунок, зная, что он симметричен относительно вертикальной оси. Напишите программу для Робота.

карт

5. Напишите программу, с помощью которой Робот сможет попасть в клетку Б во всех трех лабиринтах.

карт

6. Напишите программу, с помощью которой Робот попадет в клетку Б.

карт
 
7. Известны два вспомогательных алгоритма Робота:
 
карт

Нарисуйте, что получится при выполнении Роботом следующих основных алгоритмов:

карт

8. Составьте алгоритмы, под управлением которых Робот закрасит указанные клетки:

карт

9. Известно, что где-то правее Робота есть стена.

Составьте алгоритм, под управлением которого Робот закрасит ряд клеток до стены и вернется в исходное положение.

карт
                                
10. Известно, что где-то правее Робота есть закрашенная клетка.

карт

Составьте алгоритм, под управлением которого Робот закрасит ряд клеток до закрашенной клетки и вернется в исходное положение.

11. Известно, что Робот находится рядом с левым входом в горизонтальный коридор.

карт

Составьте алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернется в исходное положение.

12. Известно, что Робот находится где-то в горизонтальном коридоре. Ни одна из клеток коридора не закрашена.

Составьте алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернется в исходное положение.
 
карт

13. В ряду из десяти клеток правее Робота некоторые клетки закрашены.

карт

Составьте алгоритм, который закрашивает клетки:

а) ниже каждой закрашенной клетки;
б) выше и ниже каждой закрашенной клетки.

14. Что можно сказать о правильности следующего фрагмента алгоритма?

ПОКА з а крашено ДЕЛАТЬ
   ЕСЛИ справа свободно ТО
     вправо
     закрась
   КОНЕЦ
КОНЕЦ

15 Напишите программу, с помощью которой Робот сможет попасть в клетку Б во всех трех лабиринтах.

карт

16. Напишите программу, следуя которой Робот сможет пройти по коридору от левого нижнего угла поля к правому верхнему. Коридор имеет ширину одна клетка и тянется в направлении слева-снизу впра- во-вверх. Пример возможного коридора изображен на рисунке.
 
карт

Босова Л. Л., Информатика и ИКТ : учебник для 7 класса Л. Л. Босова. М. : БИНОМ. Лаборатория знаний, 2010. 229 с. : ил.

Содержание урока
 конспект урока
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.