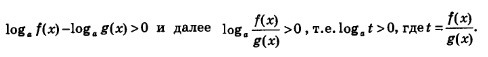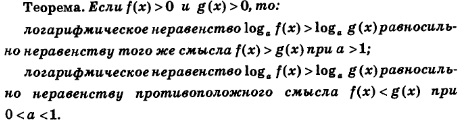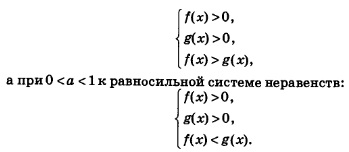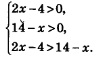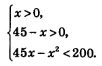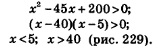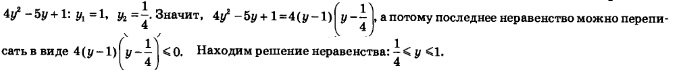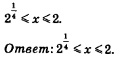Гипермаркет знаний>>Математика>>Математика 10 класс>> Логарифмические неравенства

§ 52. Логарифмические неравенства
Логарифмическими неравенствами называют неравенства вида

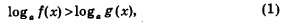
где а — положительное число, отличное от 1, и неравенства, сводящиеся к этому виду.
Для решения неравенства (1) проведем следующие рассуждения: преобразуем неравенство к виду

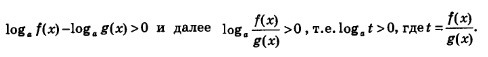
Теперь следует рассмотреть два случая: а>1 и 0<а<1. Если а > 1, то неравенство log_a t >0 имеет место тогда и только тогда, когда (см. § 49, рис. 216). Значит,

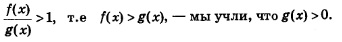
Если 0 < а < 1, то неравенство log_a t > 1 имеет место тогда и только тогда, когда 0 <t<1 (см. § 49, рис. 217). Значит,

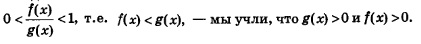
Проведенные рассуждения позволяют сформулировать следующее утверждение.

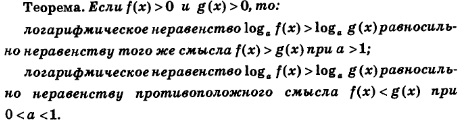
На практике эту теорему применяют так: переходят от неравенства 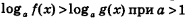к равносильной ему системе неравенств:

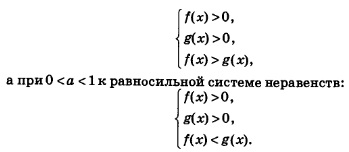
Первые два неравенства каждой из этих систем определяют область допустимых значений переменной для неравенства (1), а знак последнего неравенства каждой из систем (обратите внимание!) либо совпадает со знаком неравенства (1) — в случае, когда а> 1, — либо противоположен знаку неравенства (1) — в случае, когда0 <а <1.
Пример 1. Решить неравенства:

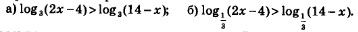
Решение. а) Область допустимых значений переменной для заданного неравенства определяется условиями: 2х-4>0 и 14-х>0. Поскольку основанием логарифмов служит число 3, а оно больше 1, то, «освобождаясь» от знаков логарифмов, мы получим неравенство того же смысла:  2х-4>14-х.
В итоге получаем систему неравенств:

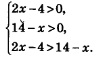
Из первого неравенства системы находим х >2, из второго — х <14, из третьего — х >6. Геометрическая модель (рис. 226) помогает найти решение системы неравенств: 6 < х < 14.
б) Здесь основание логарифма 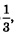, т.е. число меньше 1. Значит, соответствующая система неравенств имеет вид:

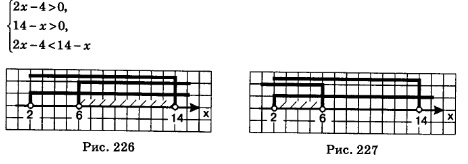
(обратите внимание: знак последнего неравенства системы противоположен знаку исходного логарифмического неравенства).
Из первого неравенства системы находим х > 2, из второго — х <14, из третьего — х <6. Геометрическая модель (рис. 227) помогает найти решение системы неравенств: 2 < х < 6.
Ответ: а) 6<х<14; 6) 2 <х <6.
Замечание. Еще раз рассмотрим систему неравенств, которая получилась в примере 1а. Третье неравенство системы имеет вид 2х -4>14-х, а второе —14 - х > 0. Но из этих двух неравенств автоматически (по свойству транзитивности неравенств) следует, что 2х - 4 > 0. Что это значит? Это значит, что первое неравенство системы с самого начала можно было отбросить без всякого ущерба для решения системы.
Рассуждая аналогично, в системе неравенств, которую мы получили в примере 16, можно было с самого начала отбросить второе неравенство.
Получив систему неравенств, математики обычно смотрят, нет ли в ней неравенства, которое логически следует из других. Если такое неравенство есть, его можно отбросить. Советуем и вам так поступать, но, разумеется, только в том случае, если вы уверены в правильности своих выводов.
Пример 2. Решить неравенство: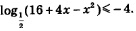
Решение. Представим -4 в виде логарифма по основанию 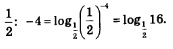  Это позволит переписать заданное неравенство в виде: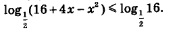
Учитывая, что здесь основанием логарифмов служит число, меньше 1, составляем равносильную заданному неравенству систему неравенств:

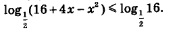
Обратите внимание: если выполняется второе неравенство системы, то автоматически выполняется и первое неравенство (если А > 16, то тем более А >0). Значит, первое неравенство системы можно отбросить. Решая второе неравенство, находим:

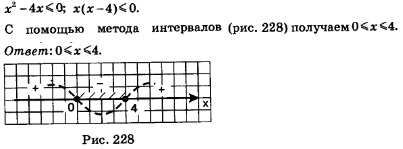
Пример 3. Решить неравенство lg х + lg(45-х)<2 +lg2.
Решение. Имеем последовательно:

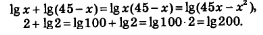
Значит, заданное неравенство можно преобразовать к виду lg(45х - х²) < 200.
«Освобождаясь» от знаков десятичных логарифмов, получим неравенство того же смысла: 45х - х² < 200. А условия, задающие область допустимых значений переменной, всегда определяют по исходному неравенству; в данном примере они таковы: х>0 и 45-х>0. В итоге получаем систему неравенств:

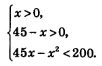
Первые два неравенства можно записать в виде двойного неравенства 0 < х < 45. Решая третье неравенство системы, находим:

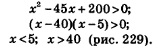
Отметив на числовой прямой эти решения совместно с полученным ранее интервалом 0 < х <45, находим их пересечение (рис. 230), т.е. решение составленной выше системы неравенств: 0 < х < 5; 40 < х < 45.
Ответ:0<х<5; 40<х<45.

Пример 4. Решить неравенство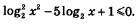

Решение. Здесь «напрашивается» введение новой переменной y =log₂ х, но сначала надо разобраться с выражением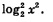
Имеем: 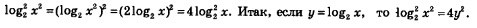  Поняв это, перепишем заданное неравенство в виде
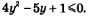
Найдем корни квадратного трехчлена

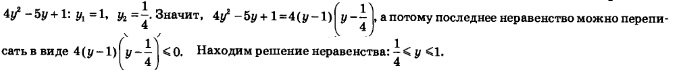
Подставив вместо у выражение log₂ х, получим: 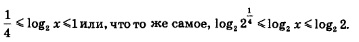 Остается «освободиться» от знаков логарифмов, сохранив имеющиеся знаки неравенств:

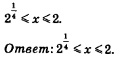
А.Г. Мордкович Алгебра 10 класс

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.