Гіпермаркет Знань>>Математика>>Математика 6 клас>> Математика: Тема 5.МНОЖЕННЯ І ДІЛЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ . Координатна площина .

Положення точки на координатній прямій визначається числом — координатою цієї точки. Положення точки на площині можна задати двома числами. Розглянемо приклад.
Місця для глядачів у залі кінотеатру можна задавати парою чисел: перше число вказує на номер ряду, а друге — на номер крісла у цьому ряді (рис. 69). До того ж, місця (3; 7) і (7; 3) — різні: перше є кріслом у третьому ряді за номером 7, а друге — кріслом у сьомому ряді за номером 3.

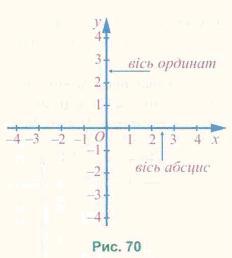
Проведемо дві перпендикулярні координатні прямі, які перетинаються в початку їх відліку — точці О й мають рівні одиничні відрізки (рис. 70). Ці прямі називають осями координат, точку О — початком координат. Горизонтальну координатну пряму називають віссю абсцис і позначають буквою х, вертикальну координатну пряму називають віссю ординат і позначають буквою у.
Вісь абсцис і вісь ординат утворюють прямокутну систему координат. Площину, на якій задана прямокутна система координат, називають координатною площиною.

Нехай А — точка координатної площини (рис. 71). Проведемо через неї пряму Ь, перпендикулярну до осі абсцис, і пряму с, перпендикулярну до осі ординат. Нехай у перетині з віссю абсцис одержимо точку В з координатою -3, а в перетині з віссю ординат — точку С з координатою 2.

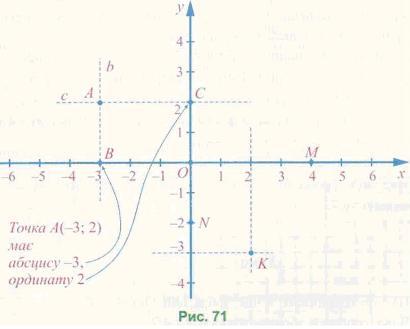
Положення точки А на координатній площині визначається парою чисел (-3; 2), які називаються координатами цієї точки. Координати точки записують у дужках: А(-3; 2), читають: точка А з координатами -3 і 2. Першу координату точки А (число -3) називають абсцисою цієї точки, а другу координату (число 2) —
 
ординатою. Точка К (рис. 71), навпаки, має абсцису 2 й ординату -3, тому К(2; -3) (на першому місці завжди записують абсцису точки, а на другому — її ординату).
Якщо точка лежить на осі абсцис, то її ордината дорівнює нулю; якщо точка лежить на осі ординат, то її абсциса дорівнює нулю. Точки М i N (рис. 71) мають координати: M(4; 0), N(0; -2).

Отже, кожній точці координатної площини відповідає одна пара чисел — її абсциса й ордината. Навпаки, будь-якій упорядкованій парі чисел відповідає одна точка площини, для якої ці числа є координатами.
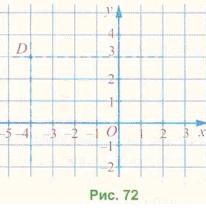
Щоб побудувати, наприклад, точку D(-4; 3), можна провести перпендикулярну пряму до осі х у точці (-4; 0) і перпендикулярну пряму до осі у в точці (0; 3) (рис. 72). Точка О перетину цих прямих має координати (-4; 3). Побудувати точку D(-4; 3) можна також, відрахувавши від точки О ліворуч 4 одиниці, а потім від одержаної точки вгору 3 одиниці.
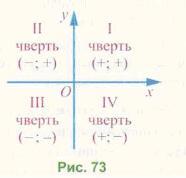
Осі координат розбивають площину на 4 частини, які називають координатними чвертями. Нумерація чвертей і знаки координат точок у кожній чверті показані на рисунку 73.


                                                                           Усно

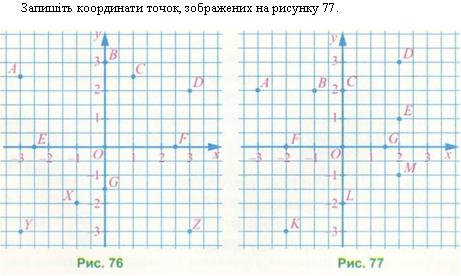
1331.   а) Назвіть координати точок, зображених на рисунку 77.
б)    Чому дорівнює абсциса точки А; С; М ?
в)    Чому дорівнює ордината точки О; N; О?
г)    Назвіть абсциси точок, що лежать на осі ординат.
д)    Назвіть точки, ординати яких дорівнюють 0.
е)    У якій чверті лежить точка О; С; А; Е?

Рівень А

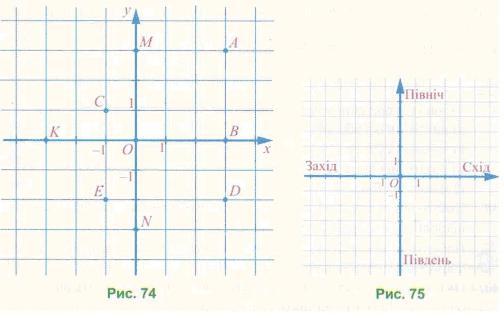
1332.    Табір туристів розташований у точці О (рис. 75), довжині однієї клітинки
відповідає відстань 1 км. Знайдіть координати місця, в яке прийдуть тури-
сти, вийшовши з табору та пройшовши:
а) 4 км на захід і 3 км на південь;     б) 3 км на схід і 5 км на північ; в) 2 км на захід і 4 км на північ;       г) 2 км на схід.
1333.    Запишіть координати точок, зображених на рисунку 76.
1334.

Побудуйте систему координат, узявши одиничний відрізок завдовжки 1 см, і позначте точки:
1335.  4(2; 1); Я(-1; -3); ОТО; -2); Д5; 0); М(-5; 1); МЗ; -5).
1336. 4(4; -1), В(-Л; -1), С(5; -3), 0(5; 2), М(-2; 0), /У(0; 4).
1337.    Запишіть координати трьох точок, які:
а)    належать осі абсцис;
б)    належать осі ординат;
в)    мають ординату 3;
г)    мають абсцису -2.
1338.    Побудуйте точку 4(-3; 5) і точку, координатами якої є числа, протилежні
відповідним координатам точки А.
1339.  Побудуйте точку С(-4; -1) і точку, координати якої дорівнюють модулям відповідних координат точки С.
 
1340.   На координатній площині побудуйте кілька точок, які мають рівні абсциси й ординати. Чи лежать ці точки на одній прямій?
 
1341.   На координатній площині побудуйте кілька точок, що мають ординату 4. Чи лежать ці точки на одній прямій?
1342.  На координатній площині накресліть трикутник КЬМ, якщо К(-3; -1), Д1;-1),М(0; 3).
1343. Побудуйте на координатній площині точки 4(5; 0), /5(4; 3), С(3; 4), ДО; 5), Е(-3; 4), К(-4; 3), Ц-5; 0), М(-4; -3), N(-3; -4), Р(0; -5), Д(3; -4), £(4; -3) та коло із центром у точці О радіусом 5 одиничних відрізків. Переконайтеся, що побудовані точки лежать на цьому колі.


Рівень Б

1344. На координатній площині проведіть пряму, що проходить через точки С(-2; 0) і Д4; 3). Позначте на цій прямій точки, абсциси яких дорівнюють -4; 0; 1. Запишіть координати одержаних точок.

1345. На координатній площині проведіть пряму, що проходить через точ 4 (-2; -3) і В(2; 5). Позначте на цій прямій точки з ординатами -1; 1; Запишіть координати одержаних точок.
 
1346.  Дано координати трьох послідовних вершин прямокутника КЬМИ: /Д-1,5;-2),Д-1,5; 1)ІМ(3; 1).
а)    Накресліть цей прямокутник.
б)    Запишіть координати точки N.
в)    Знайдіть пепиметп і площу прямокутника.
 

1347. Точки 4(3; -1) і В(-1; -1) — дві сусідні вершини квадрата АВСВ, ордин; та вершини С більша від ординати вершини В.
а)    Накресліть квадрат АВСВ.
б)    Запишіть координати точок С і О.
в)    Знайдіть периметр і площу квадрата.
 
Позначте частину координатної площини, яку утворюють точки Р(х;у), якщо:
1348.   а)х>0,у>0;    б)х>0,у = 0;    в) х < 0, |у| < 1.
 
1349.   а)х = 0,у<0;    б)х<0,.у>0;    в) |х| < 1,у > 0.
 

                                                                                    Здогадайтеся

1350. Михайлик запросив Марійку грати в таку гру: з ящика із двома білими кулями й однією чорною витягається навмання дві кулі. Якщо кулі одного кольору, то перемагає Марійка, якщо різного — Михайлик. Чи є ця гра справедливою?

Цікаві розповіді
З історії системи координат
Координати були потрібні астрономам і географам для визначення положення світил на небі й певних пунктів на Землі, для складання зоряних і географічних карт.
Прямокутна система координат у вигляді квадратної сітки (палетки) була відома ще у стародавньому Єгипті, нею користувалися і художники доби Відродження.
Ідея застосування координат у математиці належить вже згадуваному французькому математику Рене Декарту. На честь Декарта прямокутну систему координат називають ще прямокутною декартовою системою координаТ.
Термін абсциса походить від латинського слова ardinatus, що означає від>-різаний, відокремлений, а буквально перекладається як «відрізок» (на осі х).
Слово ордината походить від латинського слова ага'іпаіиз — упорядкований.
Ці терміни в їх сучасному розумінні увів у кінці XVII ст. німецький учений Г. Лейбніц (1646 - 1716). Щоб підркеслити рівноправність понять абсциса й ордината, Г. Лейбніц застосував термін координати, що походить від латинських слів со — з, разом, і агЛпаіш — упорядкований. Цей термін означає «узяті в певній послідовності числа, що визначають положення точки на площині».
 
                                                                       Вправи для повторення
1351.    У шостому класі навчається 32 учні. За контрольну роботу 10 балів одержали 4 учні. Скільки відсотків учнів класу одержали 10 балів?
1352.    Токар може виготовити партію деталей за 8 год, а його учень таку ж партію — за 12 год. За який час виготовлять партію деталей токар і учень, працюючи разом?
1353.    Два трактори, працюючи разом, можуть виорати поле за 2 дні. За скільки днів зможе виорати це поле другий трактор, якщо перший може виорати його за 3 дні?

_{Онлайн-бібліотека з підручниками і книгами, тести з математики, завдання з математики 6 клас, календарне планування}
Математика 6 клас Галина Янченко .Василь Кравчук вислано читачами iнтернет-сайту

 конспект уроку і опорний каркас                      
 презентація уроку 
 акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями)
 оцінювання 

Практика
 задачі та вправи,самоперевірка 
 практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання 

Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати
 фішки для допитливих
 шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати

Доповнення
 зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні 
 тематичні свята, девізи 
 статті 
 національні особливості
 словник термінів                          
 інше 

Тільки для вчителів
 ідеальні уроки 
 календарний план на рік 
 методичні рекомендації 
 програми
 обговорення

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.