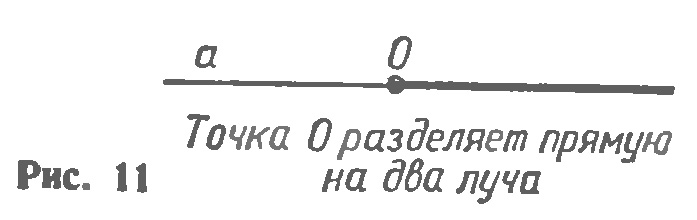Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Откладывание отрезков и углов. Полные уроки

Откладывание отрезков и углов

На рисунке изображено как с помощью линейки на полупрямой a с начальной точкой A можно отложить отрезок, длиной 3 см.

На этом рисунке изображено, как с помощью транспортира отложить от полупрямой a в верхнюю плоскость угол с градусной мерой в 60°

Сформулируем основные свойства отложения отрезков и углов:

1. на любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и только один;
2. от любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньше 180°.

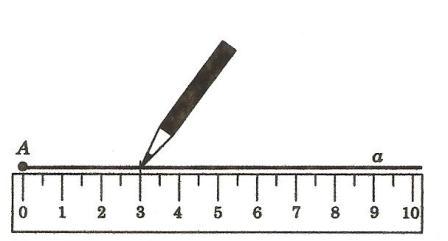
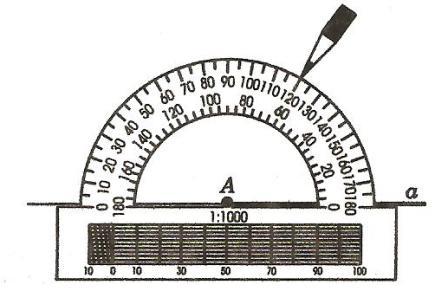
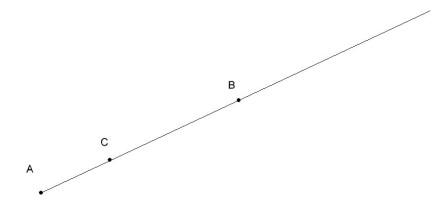
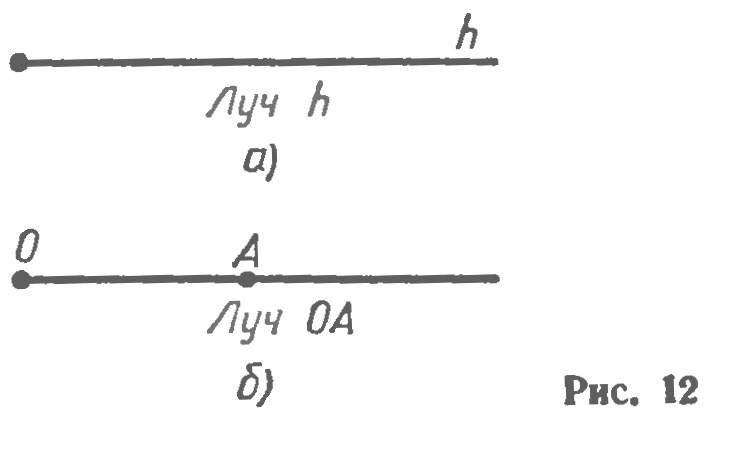
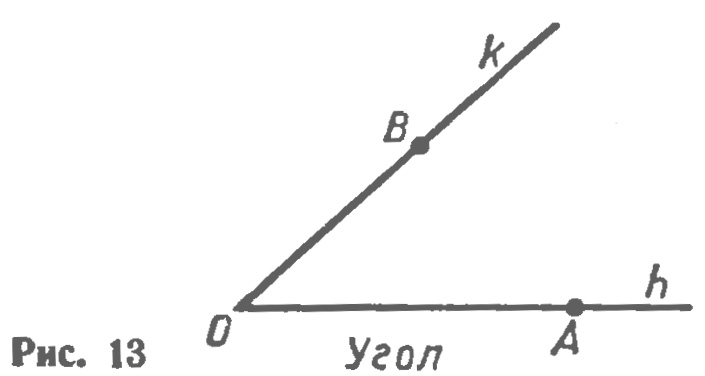
Пример решения задачи.

На луче AB отложен отрезок AC, меньший отрезка AB. Какая из трех точек A, B, C лежит между двумя другими?

Решение.
Так как точки B и C лежат на одной полупрямой с начальной точкой A, значит точкой A они не разделяются, то есть точка A не лежит между точками B и C.

Если точка B лежит между точками A и C, то было бы верно равенство: AB+BC=AC. Это невозможно, так как по условию отрезок AC меньше отрезка AB. Следовательно точка C не лежит между точками A и C.

Из трех точек A, B, C только одна лежит между двумя другими. В нашем случае: точка C расположена между точками A и B.

Луч.

Проведем прямую а и отметим на ней точку О (рис. 11).

Эта точка разделяет прямую на две части, каждая из которых называется лучом, исходящим из точки О (на рисунке 11 один из лучей выделен жирной линией). Точка О называется началом каждого из лучей. Обычно луч обозначают либо малой латинской буквой (например, луч h на рисунке 12, а), либо двумя большими латинскими буквами, первая из которых обозначает начало луча, а вторая — какую-нибудь точку на луче (например, луч ОА на рисунке 12,б).

Угол.

Напомним, что угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало — вершиной угла. На рисунке 13 изображен угол с вершиной О и сторонами h и k На сторонах отмечены точки A и В. Этот угол обозначают так: hk, или АОВ, или О.

Угол называется развернутым, если обе его стороны лежат на одной прямой. Можно сказать, что каждая сторона развернутого угла является продолжением другой стороны. На рисунке 14 изображен развернутый угол с вершиной С и сторонами р и q.

Любой угол разделяет плоскость на две части. Если угол неразвернутый, то одна из частей называется внутренней, а другая — внешней областью этого угла (рис. 15, а). На рисунке 15, б изображен неразвернутый угол. Точки А, В, С лежат внутри этого угла (т. е. во внутренней области угла), точки D и Е — на сторонах угла, а точки Р и Q — вне угла (т. е. во внешней области угла). Если угол развернутый, то любую из двух частей, на которые он разделяет плоскость, можно считать внутренней областью угла. Фигуру, состоящую из угла и его внутренней области, также называют углом.

Если луч исходит из вершины неразвернутого угла и проходит внутри угла, то он делит этот угол на два угла. На рисунке (16,а) луч ОС делит угол АОВ на два угла: АОС и СОВ. Если угол АОВ развернутый, то любой луч ОС, не совпадающий с лучами ОА и ОВ, делит этот угол на два угла: АОС и СОВ (рис. 16,б).

Сравнение отрезков и углов.

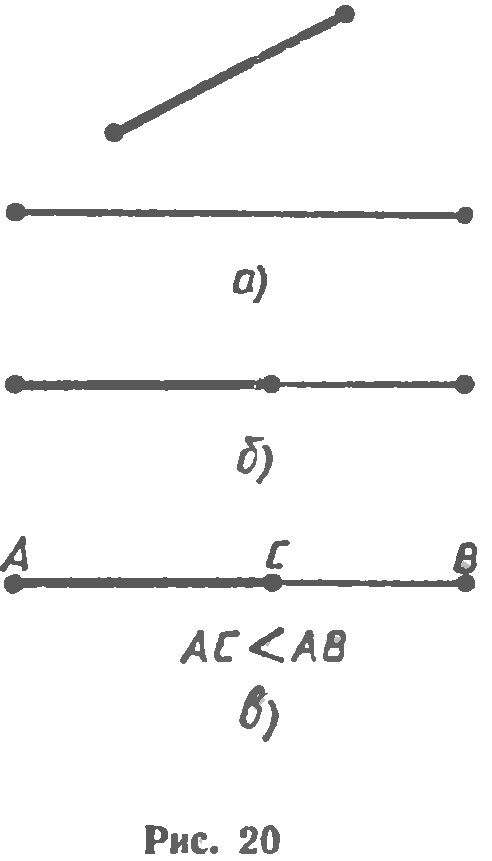
На рисунке 20, а изображены два отрезка. Чтобы установить, равны они или нет, наложим один отрезок на другой так, чтобы конец одного отрезка совместился с концом другого (рис. 20, б). Если при этом два других конца также совместятся, то отрезки полностью совместятся и, значит, они равны. Если же два других конца не совместятся, то меньшим считается тот отрезок, который составляет часть другого. На рисунке 20, в отрезок АС составляет часть отрезка АВ, поэтому отрезок АС меньше отрезка АВ (пишут так: АС<АВ).

Точка отрезка, делящая его пополам, т. е. на два равных отрезка, называется серединой отрезка. На рисунке 21 точка С середина отрезка АВ.
На рисунке 22, а изображены неразвернутые углы 1 и 2. Чтобы установить, равны они или нет, наложим один угол на другой так, чтобы сторона одного угла совместилась со стороной другого, а две другие оказались по одну сторону от совместившихся сторон (рис. 22,б). Если две другие стороны также совместятся, то углы полностью совместятся и, значит, они равны. Если же эти стороны не совместятся, то меньшим считается тот угол, который составляет часть другого. На рисунке 22,б угол 1 составляет часть угла 2, поэтому  1 < 2.
Неразвернутый угол составляет часть развернутого (рис. 23), поэтому развернутый угол больше неразвернутого угла. Любые два развернутых угла, очевидно, равны.
Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла. На рисунке 24 луч / — биссектриса угла hk.

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.