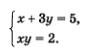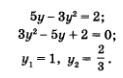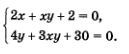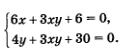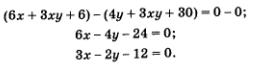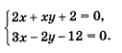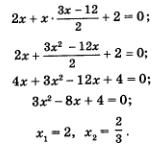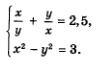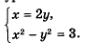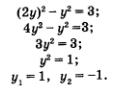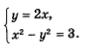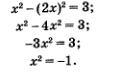|
|
|
| Строка 1: |
Строка 1: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Методы решения систем уравнений<metakeywords>Методы решения систем уравнений</metakeywords>''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Методы решения систем уравнений<metakeywords>Методы решения систем уравнений</metakeywords>''' |
| | | | |
| - | <br> | + | <br> |
| | | | |
| - | '''МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ'''<br> | + | '''МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ'''<br> |
| | | | |
| - | <br>В этом параграфе мы обсудим три метода решения систем уравнений, более надежные, чем графический метод, который рассмотрели в предыдущем параграфе.<br>'''1. Метод подстановки'''<br>Этот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений (не обязательно линейных) с двумя переменными х и у (разумеется, переменные могут быть обозначены и другими буквами, что не имеет значения). Фактически этим алгоритмом мы воспользовались в предыдущем параграфе, когда задача о двузначном числе привела к математической модели, представляющей собой систему уравнений. Эту систему уравнений мы решили выше методом подстановки (см. пример 1 из § 4).<br>'''''Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у.'''''<br>'''1.''' Выразить у через х из одного уравнения системы.<br>'''2.''' Подставить полученное выражение вместо у в другое уравнение системы.<br>'''3.''' Решить полученное уравнение относительно х.<br>'''4.''' Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.<br>'''5.''' Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге.<br>Переменные х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой.<br>'''Пример 1.''' Решить систему уравнений [[Image:al61.jpg]]<br>'''Р е ш е н и е. 1)''' Выразим х через у из первого уравнения системы: х = 5 - 3у.<br>'''2) ''' Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2.<br>'''3) ''' Решим полученное уравнение: [[Image:al62.jpg]]<br>'''4)''' Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если [[Image:al63.jpg]] то [[Image:al64.jpg]]<br>'''5)''' Пары (2; 1) и [[Image:al65.jpg]] решения заданной системы уравнений. | + | <br>В этом параграфе мы обсудим три метода решения систем уравнений, более надежные, чем графический метод, который рассмотрели в предыдущем параграфе.<br>'''1. Метод подстановки'''<br>Этот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений (не обязательно линейных) с двумя переменными х и у (разумеется, переменные могут быть обозначены и другими буквами, что не имеет значения). Фактически этим алгоритмом мы воспользовались в предыдущем параграфе, когда задача о двузначном числе привела к математической модели, представляющей собой систему уравнений. Эту систему уравнений мы решили выше методом подстановки (см. пример 1 из § 4).<br>'''''Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у.'''''<br>'''1.''' Выразить у через х из одного уравнения системы.<br>'''2.''' Подставить полученное выражение вместо у в другое уравнение системы.<br>'''3.''' Решить полученное уравнение относительно х.<br>'''4.''' Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.<br>'''5.''' Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге.<br>Переменные х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой.<br>'''Пример 1.''' Решить систему уравнений [[Image:Al61.jpg]]<br>'''Р е ш е н и е. 1)''' Выразим х через у из первого уравнения системы: х = 5 - 3у.<br>'''2) ''' Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2.<br>'''3) ''' Решим полученное уравнение: [[Image:Al62.jpg]]<br>'''4)''' Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если [[Image:Al63.jpg]] то [[Image:Al64.jpg]]<br>'''5)''' Пары (2; 1) и [[Image:Al65.jpg]] решения заданной системы уравнений. |
| | | | |
| - | '''О тв е т:''' (2; 1); [[Image:al65.jpg]]<br>'''2. Метод алгебраического сложения'''<br>Этот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода напомним на следующем примере.<br>'''Пример 2.''' Решить систему уравнений [[Image:al66.jpg]]<br>'''Решение.''' Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения: [[Image:al67.jpg]]<br>Вычтем второе уравнение системы из ее первого уравнения: | + | '''О тв е т:''' (2; 1); [[Image:Al65.jpg]]<br>'''2. Метод алгебраического сложения'''<br>Этот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода напомним на следующем примере.<br>'''Пример 2.''' Решить систему уравнений [[Image:Al66.jpg]]<br>'''Решение.''' Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения: [[Image:Al67.jpg]]<br>Вычтем второе уравнение системы из ее первого уравнения: |
| | | | |
| - | [[Image:al68.jpg]]<br>В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой: [[Image:al69.jpg]]<br>Эту систему можно решить методом подстановки. Из второго уравнения находим [[Image:al610.jpg]] Подставив это выражение вместо у в первое уравнение системы, получим | + | [[Image:Al68.jpg]]<br>В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой: [[Image:Al69.jpg]]<br>Эту систему можно решить методом подстановки. Из второго уравнения находим [[Image:Al610.jpg]] Подставив это выражение вместо у в первое уравнение системы, получим |
| | | | |
| - | [[Image:al611.jpg]]<br>Осталось подставить найденные значения х в формулу [[Image:al612.jpg]] | + | [[Image:Al611.jpg]]<br>Осталось подставить найденные значения х в формулу [[Image:Al612.jpg]] |
| | | | |
| - | Если х = 2, то [[Image:al613.jpg]]<br>Таким образом, мы нашли два решения системы: [[Image:al614.jpg]] | + | Если х = 2, то [[Image:Al613.jpg]]<br>Таким образом, мы нашли два решения системы: [[Image:Al614.jpg]] |
| | | | |
| - | '''Ответ:''' [[Image:al615.jpg]] | + | '''Ответ:''' [[Image:Al615.jpg]] |
| | | | |
| - | '''3. Метод введения новых переменных'''<br>С методом введения новой переменной при решении рациональных уравнений с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах.<br>Пример 3. Решить систему уравнений<br>— + — = 2,5, У х<br>х2 - у2 = 3.<br>х<br>Решение. Введем новую переменную *--• Тогда первое<br>У<br>уравнение системы можно будет переписать в более простом виде: Ь + ~ = 2,5. Решим это уравнение относительно переменной I:<br>I 2<br>2;2 + 2 - ы _ л 21<br>2*2 -5* +2 = 0;<br>Оба эти значения удовлетворяют условию 21Ф 0, а потому являются корнями рационального уравнения с переменной I.<br>X X<br>Но I = - , значит, либо — = 2, откуда находим, что х = 2у, либо У У<br>х 1<br>— = - , откуда находим, что у = 2х. У 2<br>Таким образом, с помощью метода введения новой переменной нам удалось как бы «расслоить» первое уравнение системы, достаточно сложное по виду, на два более простых уравнения:<br>х=2у; у — 2х.<br> | + | '''3. Метод введения новых переменных'''<br>С методом введения новой переменной при решении рациональных уравнений с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах.<br>'''Пример 3.''' Решить систему уравнений [[Image:al616.jpg]] |
| | | | |
| - | Что же дальше? А дальше каждое из двух полученных простых уравнений нужно поочередно рассмотреть в системе с уравнением х2 - у2 = 3, о котором мы пока не вспоминали. Иными словами, задача сводится к решению двух систем уравнений:<br>50<br>2.5.<br>СИСТЕМЫ УРАВНЕНИИ<br>х = 2 у, Г у = 2х,<br>х2 - у2 = 3; \х2 - у2 = 3. Надо найти решения первой системы, второй системы и все полученные пары значений включить в ответ. Решим первую систему уравнений:<br>х = 2 у, х2 - у2 = 3.<br>Воспользуемся методом подстановки, тем более что здесь для него все готово: подставим выражение 2у вместо х во второе уравнение системы. Получим<br>(2у)2-у2 = 3; 4 У2 - у2 —3; Зу2 = 3; У2 = 1; 2/1 = !> У2 = -1-<br>Так как х = 2у, то находим соответственно хх = 2, х2 = -2. Тем самым получены два решения заданной системы: (2; 1) и (-2; -1). Решим вторую систему уравнений:<br>у = 2х,<br>х2 - у2 = 3.<br>Снова воспользуемся методом подстановки: подставим выражение 2х вместо у во второе уравнение системы. Получим<br>х2-(2х)2 = 3; х2 -4.x2 = 3; -Зх2 = 3; х2 = -1.<br>Это уравнение не имеет корней, значит, и система уравнений не имеет решений. Таким образом, в ответ надо включить только решения первой системы.<br>Ответ: (2; 1); (-2;-1).<br>Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах. Первый вариант: вводится одна новая переменная и используется только в одном<br>4*<br>51<br>2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br>уравнении системы. Именно так обстояло дело в примере 3. Второй вариант: вводятся две новые переменные и используются одновременно в обоих уравнениях системы. Так будет обстоять дело в примере 4.<br>Пример 4. Решить систему уравнений 2 3<br>х-3у 8<br>2 х + у 9<br>= 2, = 1.<br>х-3у 2 х + у Решение. Введем две новые переменные: а =<br>6 =<br>Учтем, что тогда<br>8<br>х-3 у<br>- 4а,<br>= 36.<br>2х + у ' х-Зу " ' х ~ Зу<br>Это позволит переписать заданную систему в значительно более простом виде, но относительно новых переменных а и Ь:<br>\а + Ь = 2,<br>[4а - 36 = 1.<br>Применим для решения этой системы метод алгебраического сложения:<br>ГЗа + ЗЬ = 6, [4а- 36 = 1.<br>7а =7; а=1.<br>Так как а = 1, то из уравнения а + 6 = 2 находим: 1 + 6 = 2; 6=1. Таким образом, относительно переменных а и 6 мы получили одно решение:<br>[а = 1, [6 = 1.<br>Возвращаясь к переменным х и у, получаем систему уравнений<br>2<br>х-3у 3<br>2х + у<br>= 1, = 1,<br>т.е.<br>х-3 у = 2, 2х + у = 3.<br>52<br>2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br>Применим для решения этой системы метод алгебраического сложения:<br>+ Г*-3 у-2, [6х + 3у = 9.<br>7х = 11; 11<br>11<br>И 7 22<br>Так как х = у, то из уравнения 2* + у = 3 находим: у~3-2х =<br>= 3-2-у=3- ?<br>Таким образом, относительно перемен-<br>ных хиу мы получили одно решение:<br>11<br>1<br><br>Ответ:<br>Г11 1<br>7 ' 7<br>обратите внимание<br>равносильность систем уравнений<br>Завершим этот параграф кратким, но достаточно серьезным теоретическим разговором. Вы уже накопили некоторый опыт в решении различных уравнений: линейных, квадратных, рациональных, иррациональных. Вы знаете, что основная идея решения уравнения состоит в постепенном переходе от одного уравнения к другому, более простому, но равносильному заданному. В предыдущем параграфе мы ввели понятие равносильности для уравнений с двумя переменными. Используют это понятие и для систем уравнений.<br>Определение. Две системы уравнений с переменными х и у называют равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.<br>Все три метода (подстановки, алгебраического сложения и введения новых переменных), которые<br>53<br>
| + | '''Решение.''' Введем новую переменную [[Image:al617.jpg]] Тогда первое уравнение системы можно будет переписать в более простом виде: [[Image:al618.jpg]] Решим это уравнение относительно переменной t: |
| | | | |
| - | 2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br>мы обсудили в этом параграфе, абсолютно корректны с точки зрения равносильности. Иными словами, используя эти методы, мы заменяем одну систему уравнений другой, более простой, но равносильной первоначальной системе.<br>
| + | [[Image:al619.jpg]]<br>Оба эти значения удовлетворяют условию [[Image:al620.jpg]], а потому являются корнями рационального уравнения с переменной t.<br>Но [[Image:al621.jpg]] значит, либо [[Image:al622.jpg]] откуда находим, что х = 2у, либо [[Image:al623.jpg]]<br>Таким образом, с помощью метода введения новой переменной нам удалось как бы «расслоить» первое уравнение системы, достаточно сложное по виду, на два более простых уравнения:<br>х = 2 у; у — 2х.<br> |
| | | | |
| - | <br> | + | Что же дальше? А дальше каждое из двух полученных простых уравнений нужно поочередно рассмотреть в системе с уравнением х<sup>2</sup> - у<sup>2</sup> = 3, о котором мы пока не вспоминали. Иными словами, задача сводится к решению двух систем уравнений: |
| | + | |
| | + | [[Image:al624.jpg]] |
| | + | |
| | + | Надо найти решения первой системы, второй системы и все полученные пары значений включить в ответ. Решим первую систему уравнений: |
| | + | |
| | + | [[Image:al625.jpg]]<br>Воспользуемся методом подстановки, тем более что здесь для него все готово: подставим выражение 2у вместо х во второе уравнение системы. Получим [[Image:al626.jpg]]<br>Так как х = 2у, то находим соответственно х<sub>1</sub> = 2, х<sub>2</sub> = 2. Тем самым получены два решения заданной системы: (2; 1) и (-2; -1). Решим вторую систему уравнений: [[Image:al627.jpg]]<br>Снова воспользуемся методом подстановки: подставим выражение 2х вместо у во второе уравнение системы. Получим [[Image:al628.jpg]]<br>Это уравнение не имеет корней, значит, и система уравнений не имеет решений. Таким образом, в ответ надо включить только решения первой системы.<br>'''Ответ:''' (2; 1); (-2;-1).<br>Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах. '''''Первый вариант:''''' вводится одна новая переменная и используется только в одном уравнении системы. Именно так обстояло дело в примере 3.'''''Второй вариант:''''' вводятся две новые переменные и используются одновременно в обоих уравнениях системы. Так будет обстоять дело в примере 4.<br>'''Пример 4.''' Решить систему уравнений 2 3<br>х-3у 8<br>2 х + у 9<br>= 2, = 1.<br>х-3у 2 х + у Решение. Введем две новые переменные: а =<br>6 =<br>Учтем, что тогда<br>8<br>х-3 у<br>- 4а,<br>= 36.<br>2х + у ' х-Зу " ' х ~ Зу<br>Это позволит переписать заданную систему в значительно более простом виде, но относительно новых переменных а и Ь:<br>\а + Ь = 2,<br>[4а - 36 = 1.<br>Применим для решения этой системы метод алгебраического сложения:<br>ГЗа + ЗЬ = 6, [4а- 36 = 1.<br>7а =7; а=1.<br>Так как а = 1, то из уравнения а + 6 = 2 находим: 1 + 6 = 2; 6=1. Таким образом, относительно переменных а и 6 мы получили одно решение:<br>[а = 1, [6 = 1.<br>Возвращаясь к переменным х и у, получаем систему уравнений<br>2<br>х-3у 3<br>2х + у<br>= 1, = 1,<br>т.е.<br>х-3 у = 2, 2х + у = 3.<br>52<br>2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br>Применим для решения этой системы метод алгебраического сложения:<br>+ Г*-3 у-2, [6х + 3у = 9.<br>7х = 11; 11<br>11<br>И 7 22<br>Так как х = у, то из уравнения 2* + у = 3 находим: у~3-2х =<br>= 3-2-у=3- ?<br>Таким образом, относительно перемен-<br>ных хиу мы получили одно решение:<br>11<br>1<br><br>Ответ:<br>Г11 1<br>7 ' 7<br>обратите внимание<br>равносильность систем уравнений<br>Завершим этот параграф кратким, но достаточно серьезным теоретическим разговором. Вы уже накопили некоторый опыт в решении различных уравнений: линейных, квадратных, рациональных, иррациональных. Вы знаете, что основная идея решения уравнения состоит в постепенном переходе от одного уравнения к другому, более простому, но равносильному заданному. В предыдущем параграфе мы ввели понятие равносильности для уравнений с двумя переменными. Используют это понятие и для систем уравнений.<br>Определение. Две системы уравнений с переменными х и у называют равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.<br>Все три метода (подстановки, алгебраического сложения и введения новых переменных), которые<br>53<br> |
| | + | |
| | + | 2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br>мы обсудили в этом параграфе, абсолютно корректны с точки зрения равносильности. Иными словами, используя эти методы, мы заменяем одну систему уравнений другой, более простой, но равносильной первоначальной системе.<br> |
| | + | |
| | + | <br> |
| | | | |
| | А.Г. Мордкович Алгебра 9 класс | | А.Г. Мордкович Алгебра 9 класс |
Версия 07:22, 29 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Методы решения систем уравнений
МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
В этом параграфе мы обсудим три метода решения систем уравнений, более надежные, чем графический метод, который рассмотрели в предыдущем параграфе.
1. Метод подстановки
Этот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений (не обязательно линейных) с двумя переменными х и у (разумеется, переменные могут быть обозначены и другими буквами, что не имеет значения). Фактически этим алгоритмом мы воспользовались в предыдущем параграфе, когда задача о двузначном числе привела к математической модели, представляющей собой систему уравнений. Эту систему уравнений мы решили выше методом подстановки (см. пример 1 из § 4).
Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у.
1. Выразить у через х из одного уравнения системы.
2. Подставить полученное выражение вместо у в другое уравнение системы.
3. Решить полученное уравнение относительно х.
4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.
5. Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге.
Переменные х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой.
Пример 1. Решить систему уравнений 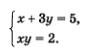
Р е ш е н и е. 1) Выразим х через у из первого уравнения системы: х = 5 - 3у.
2) Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2.
3) Решим полученное уравнение: 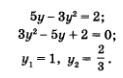
4) Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если 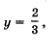 то то 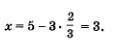
5) Пары (2; 1) и 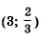 решения заданной системы уравнений. решения заданной системы уравнений.
О тв е т: (2; 1); 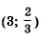
2. Метод алгебраического сложения
Этот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода напомним на следующем примере.
Пример 2. Решить систему уравнений 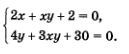
Решение. Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения: 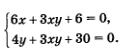
Вычтем второе уравнение системы из ее первого уравнения:
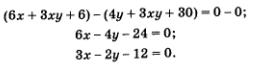
В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой: 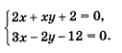
Эту систему можно решить методом подстановки. Из второго уравнения находим 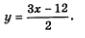 Подставив это выражение вместо у в первое уравнение системы, получим Подставив это выражение вместо у в первое уравнение системы, получим
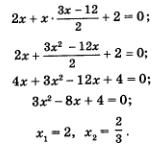
Осталось подставить найденные значения х в формулу 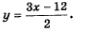
Если х = 2, то 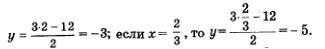
Таким образом, мы нашли два решения системы: 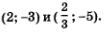
Ответ: 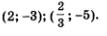
3. Метод введения новых переменных
С методом введения новой переменной при решении рациональных уравнений с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах.
Пример 3. Решить систему уравнений 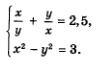
Решение. Введем новую переменную 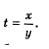 Тогда первое уравнение системы можно будет переписать в более простом виде: Тогда первое уравнение системы можно будет переписать в более простом виде: 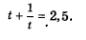 Решим это уравнение относительно переменной t: Решим это уравнение относительно переменной t:

Оба эти значения удовлетворяют условию 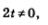 , а потому являются корнями рационального уравнения с переменной t. , а потому являются корнями рационального уравнения с переменной t.
Но 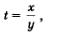 значит, либо значит, либо 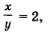 откуда находим, что х = 2у, либо откуда находим, что х = 2у, либо 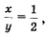
Таким образом, с помощью метода введения новой переменной нам удалось как бы «расслоить» первое уравнение системы, достаточно сложное по виду, на два более простых уравнения:
х = 2 у; у — 2х.
Что же дальше? А дальше каждое из двух полученных простых уравнений нужно поочередно рассмотреть в системе с уравнением х2 - у2 = 3, о котором мы пока не вспоминали. Иными словами, задача сводится к решению двух систем уравнений:
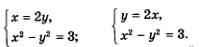
Надо найти решения первой системы, второй системы и все полученные пары значений включить в ответ. Решим первую систему уравнений:
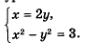
Воспользуемся методом подстановки, тем более что здесь для него все готово: подставим выражение 2у вместо х во второе уравнение системы. Получим 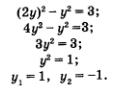
Так как х = 2у, то находим соответственно х1 = 2, х2 = 2. Тем самым получены два решения заданной системы: (2; 1) и (-2; -1). Решим вторую систему уравнений: 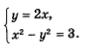
Снова воспользуемся методом подстановки: подставим выражение 2х вместо у во второе уравнение системы. Получим 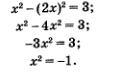
Это уравнение не имеет корней, значит, и система уравнений не имеет решений. Таким образом, в ответ надо включить только решения первой системы.
Ответ: (2; 1); (-2;-1).
Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах. Первый вариант: вводится одна новая переменная и используется только в одном уравнении системы. Именно так обстояло дело в примере 3.Второй вариант: вводятся две новые переменные и используются одновременно в обоих уравнениях системы. Так будет обстоять дело в примере 4.
Пример 4. Решить систему уравнений 2 3
х-3у 8
2 х + у 9
= 2, = 1.
х-3у 2 х + у Решение. Введем две новые переменные: а =
6 =
Учтем, что тогда
8
х-3 у
- 4а,
= 36.
2х + у ' х-Зу " ' х ~ Зу
Это позволит переписать заданную систему в значительно более простом виде, но относительно новых переменных а и Ь:
\а + Ь = 2,
[4а - 36 = 1.
Применим для решения этой системы метод алгебраического сложения:
ГЗа + ЗЬ = 6, [4а- 36 = 1.
7а =7; а=1.
Так как а = 1, то из уравнения а + 6 = 2 находим: 1 + 6 = 2; 6=1. Таким образом, относительно переменных а и 6 мы получили одно решение:
[а = 1, [6 = 1.
Возвращаясь к переменным х и у, получаем систему уравнений
2
х-3у 3
2х + у
= 1, = 1,
т.е.
х-3 у = 2, 2х + у = 3.
52
2.6. I
СИСТЕМЫ УРАВНЕНИЙ
Применим для решения этой системы метод алгебраического сложения:
+ Г*-3 у-2, [6х + 3у = 9.
7х = 11; 11
11
И 7 22
Так как х = у, то из уравнения 2* + у = 3 находим: у~3-2х =
= 3-2-у=3- ?
Таким образом, относительно перемен-
ных хиу мы получили одно решение:
11
1
Ответ:
Г11 1
7 ' 7
обратите внимание
равносильность систем уравнений
Завершим этот параграф кратким, но достаточно серьезным теоретическим разговором. Вы уже накопили некоторый опыт в решении различных уравнений: линейных, квадратных, рациональных, иррациональных. Вы знаете, что основная идея решения уравнения состоит в постепенном переходе от одного уравнения к другому, более простому, но равносильному заданному. В предыдущем параграфе мы ввели понятие равносильности для уравнений с двумя переменными. Используют это понятие и для систем уравнений.
Определение. Две системы уравнений с переменными х и у называют равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.
Все три метода (подстановки, алгебраического сложения и введения новых переменных), которые
53
2.6. I
СИСТЕМЫ УРАВНЕНИЙ
мы обсудили в этом параграфе, абсолютно корректны с точки зрения равносильности. Иными словами, используя эти методы, мы заменяем одну систему уравнений другой, более простой, но равносильной первоначальной системе.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|