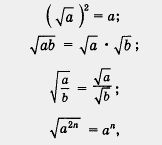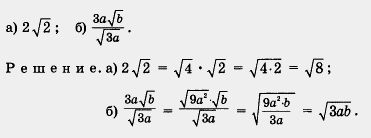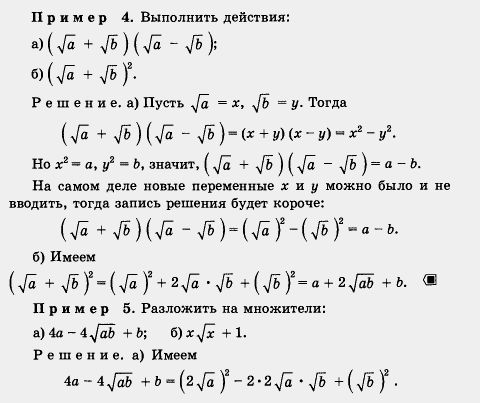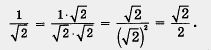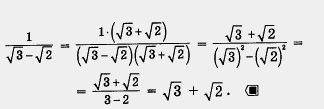Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Преобразование выражений, содержащих операцию извлечения квадратного корня

Преобразование выражений, содержащих операцию извлечения квадратного корня

До сих пор мы с вами выполняли преобразования только рациональных выражений, используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т. д. В этой главе мы ввели новую операцию — операцию извлечения квадратного корня; мы установили, что

где, напомним, a, b — неотрицательные числа.

Используя эти формулы, можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.

Пример 3. Внести множитель под знак квадратного корня:

Пример 6. Упростить выражение Решение. Выполним последовательные преобразования:

Пример 7. Преобразовать заданное алгебраическое выражение к такому виду, чтобы знаменатель дроби не содержал знаков квадратных корней:

Решение. В обоих случаях воспользуемся к тем, что значение дроби не изменится, если ее числитель и знаменатель одновременно умножить на одно и то же отличное от нуля число  или выражение.

а) Умножив числитель и знаменатель дроби на  , получим

б) Умножив числитель и знаменатель дроби на получим

Если знаменатель алгебраической дроби содержит знак квадратного корня, то обычно говорят, что в знаменателе содержится иррациональность (почему используется именно такой термин, мы обсудим позднее, в § 27).

Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют обычно освобождением от иррациональности в знаменателе. Два основных приема освобождения от иррациональности в знаменателе мы как раз и рассмотрели в примере если знаменатель имеет вид , то числитель и знаменатель дроби следует умножить на  если знаменатель имеет вид , то числитель и знаменатель дроби надо умножить соответственно на .

Зачем нужно уметь освобождаться от иррациональности в знаменателе? Во многих случаях это облегчает тождественные преобразования алгебраических выражений, в чем мы сейчас и убедимся.

Пример 8. Упростить выражение

Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.

_{Материалы по математике за 8 класс скачать, конспект по математике , учебники и книги скатать бесплатно, школьная программа онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.