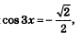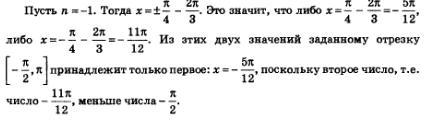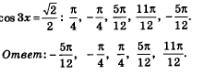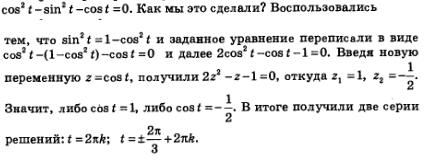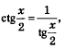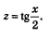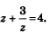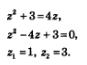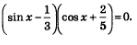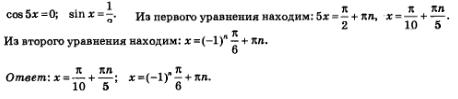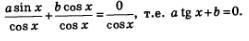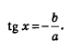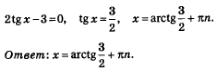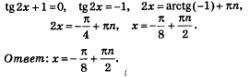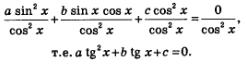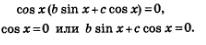|
|
|
| (11 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>>Математика: Тригонометрические уравнения<metakeywords>Тригонометрические уравнения</metakeywords>'''
| + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 10 класс, уроки математики, тригонометрические уравнения, функции</metakeywords> |
| | | | |
| - | <br>
| + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>> Тригонометрические уравнения''' |
| | | | |
| - | '''§ 20. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ'''<br>1. Простейшие тригонометрические уравнения<br>Тригонометрическими уравнениями обычно называют уравнения, в которых переменная содержится под знаками тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида a[[Image:alga331.jpg]] — действительное число. К настоящему моменту мы знаем, что:<br>1) если | а | < 1, то решения уравнения соз о:-а имеют вид: | + | '''§ 20. Тригонометрические уравнения''' |
| | | | |
| - | [[Image:alga332.jpg]] <br>Во всех перечисленных формулах подразумевается, что параметр (n, к и т.д.) принимает любые целочисленные значения [[Image:alga333.jpg]]<br>К простейшим относят обычно и уравнения вида Т(кх + m)=а, где Т — знак какой-либо тригонометрической функции.<br>'''Пример 1.''' Решить уравнения:
| + | <h2>Простейшие тригонометрические уравнения</h2> |
| | | | |
| - | [[Image:alga334.jpg]]<br>'''Решение:''' а) Введем новую переменную [[Image:alga335.jpg]]<br>Возвращаясь к переменной х, получаем: [[Image:alga336.jpg]] Осталось обе части этого равенства разделить почленно на 2; получим:
| + | Все уравнения, которые содержат переменную под знаком тригонометрических функций, называются тригонометрическим уравнением. Если перед вами уравнения такого вида, как: |
| | | | |
| - | [[Image:alga337.jpg]]<br>Заметим, что при наличии некоторого опыта можно не вводить промежуточную переменную t = 2х, а сразу переходить от уравнения [[Image:alga338.jpg]]<br>Именно так мы и будем действовать в дальнейшем.<br>б) Мы знаем, что решения уравнения соs t = а имеют вид:[[Image:alga339.jpg]] Для нашего примера это означает, что
| + | sin x = a; cos x = a; tg x = a; ctg x = a, |
| | | | |
| - | [[Image:alga340.jpg]]<br>'''Пример 2.''' Найти те корни уравнения [[Image:alga341.jpg]] которые принадлежат отрезку[0, п].<br>'''Решение.''' Сначала решим уравнение в общем виде: [[Image:alga342.jpg]] (см. пример 1а). Далее придадим параметру п последовательно значения 0,1, 2,..., -1, -2,... и подставим эти значения в общую формулу корней.<br>[[Image:alga343.jpg]]<br>Это число не принадлежит заданному отрезку [0, п]. Тем более не будут принадлежать заданному отрезку те значения х, которые получаются из общей формулы при n = -2, -3,...<br>На рис. 94 представлена геометрическая интерпретация проведенных рассуждений.<br>
| + | в котором x является его переменной, и a является действительным числом, то такие уравнения называются простейшими тригонометрическими уравнениями. |
| | + | И если нам с вами известно, что в том случае, когда: |
| | | | |
| - | [[Image:alga344.jpg]]<br>Итак, заданному отрезку [0, п] принадлежат те корни уравнения, которые получаются из общей формулы при следующих значениях параметра n: n = 0, n = 1. Эти корни таковы[[Image:alga345.jpg]]<br>'''Ответ:''' [[Image:alga345.jpg]]<br>
| + | 1) | а | < 1, то решения уравнения cos о:-а приобретает такой вот вид: |
| | | | |
| - | '''Пример 3. '''Найти те корни уравнения сое Зх =--, которые принадле-<br>2<br>жат отрезку<br>N•4<br>Решение. Сначала решим уравнение в общем виде:<br>, л 2лл<br>х=±—+-<br>4 3<br>(см. пример 16). Далее придадим параметру п последовательно значения 0,1, 2,..., -1, -2,... и подставим эти значения в общую формулу корней.<br>Если л = 0, тоя; = ±^ + 0 = ±^. Оба эти числа: ~ ~ и ~ принадлежат задан-<br>Г ■ я '<br>ному отрезку — —, л<br>гл 1 2л г, л 2л 11л -<br>Если п = 1, то х = ±— + —. Это значит, что либо х= — + — =-, либо<br>4 3 4 3 12<br>л 2л 5л „ 11л 5л<br>х = — + — = —. Оба числа:-и —<br>4 3 12 12 12<br>принадлежат заданному отрезку<br>л<br>л 4л л 4л 19л<br>Если п = 2, то х = ± — + —. Это значит, что либо х=— + — =-, либо<br>4 3 4 3 12<br>л 4л 13л 19л 13л<br>х- — + — --. Оба числа:- и- — не принадлежат заданному от-<br>4 3 12 12 12<br>резку<br>[-И<br>, поскольку оба они больше числа л. Тем более не будут при-<br>надлежать заданному отрезку те значения х, которые получаются из общей формулы при п = 3,4,...<br>гт 1 гг. , л 2л _ л 2л 5л<br>Пусть п =-1. Тогда х = ±---. Это значит, что либо х ----=--,<br>4 3 4 3 12<br>л 2л 11л „<br>либо х = ~— —— = Из зтих двух значении заданному отрезку<br>л<br><br>5л<br>принадлежит только первое: х =--, поскольку второе число, т.е.<br>X 2<br>11л л число - —, меньше числа--.<br>12 2<br>Не будут принадлежать заданному отрезку те значения х, которые получаются из общей формулы при п = -2, - 3,...<br>На рис. 95 представлена геометрическая интерпретация проведенных рассуждений.<br> 1 1 1 1 1 л 5л 1 <br> <br> 1.1. ч <br> У 0 1 р X <br> 1 <br>Рис. 96<br>92<br>Итак, заданному отрезку<br>л<br>~2'К<br>принадлежат следующие корни урав-<br>л/2 л л 5л 11л 5л<br>нения соз Зл: = —: —, —, —,-,--.<br>2 4 4 12 12 12<br>Л 5л л л 5л 11л<br>итвет:--, —, —, —, -.<br>12 4 4 12 12<br>2. Два основных метода решения тригонометрических уравнений<br>Для решения тригонометрических уравнений чаще всего используются два метода: введения новой переменной и разложения на множители.<br>Вернемся к материалу § 16. Там в примере 3 мы решили тригонометрическое уравнение 2вт2 *-5зт*+2 =0. Как мы это сделали? Ввели новую переменную г = аш *, переписали уравнение в виде<br>2гг -5г+ 2=0, откуда г1 =2, г2 =—. В результате мы получили два<br>2<br>простых уравнения: зтI =2; зт* = —. Первое уравнение не имеет<br>2<br>решений, а для второго нашли две серии решений:<br>*= —+ 2лк; *= —+ 2лк и установили (см. § 18), что эти две серии 6 6<br>можно объединить одной формулой * =(—1)" — + лп.<br>6<br>В том же § 16 в примере 4 мы решили тригонометрическое уравнение сое2 *-вт2*-соа* =0. Как мы это сделали? Воспользовались тем, что зт2*=1-со82* и заданное уравнение переписали в виде со82*-(1-со82*)-со8*=0 и далее 2созг *-соз *-1 =0. Введя новую<br>переменную г=со8*, получили 2г2 -2-1=0, откуда г1 =1, г2 =-—.<br>2<br>Значит, либо со8 * =1, либо сов* =-—. В итоге получили две серии<br>2<br>2л<br>решений: * =2пк; *=±—+2лк.<br>3<br>Рассмотрим еще один пример на использование метода введения новой переменной при решении тригонометрических уравнений.<br>X X<br>Пример 4. Решить уравнение —н Зс1§— =4.<br>2 2<br>Решение. Поскольку с1§— = —, есть смысл ввести новую переменную<br>2 <•§<br>х 3<br>г = . Это позволит переписать уравнение в более простом виде: г + — =4. 2 2<br>93<br>Имеем:<br>г2+3=4г, г2 -42 + 3=0, 2! =1, г2 =3.<br>х<br>Возвращаясь к переменной х9 получаем два уравнения: = 1 или<br>X X X тс<br>= 3. Из первого уравнения находим: — = агс1§ 1 + тел, т.е. —= —+ял,<br>К X<br>х=— + 2тсл. Из второго уравнения находим: — = агс1§ 3 + яп, х =2агс{§ 3 + 2ял. 2 2 тс<br>Ответ: х = — + 2пп, лс=2агс(еЗ + 2тсл. 2<br>V^Теперь поговорим о втором методе решения тригонометрических уравнений — методе разложения на множители. Смысл этого метода вам знаком: если уравнение х) =0 возможно преобразовать к виду /, (х) /2(х) =0, то задача сводится к решению двух уравнений (обычно говорят — к решению совокупности уравнений):<br>А(*)=0; /2(х)=0. Пример 5. Решить уравнение ||созх + ^|=0.<br>Решение. Задача сводится к решению совокупности уравнений:<br>1 2<br>81ПЛС = -; СОЗ X = —.<br>3 5<br>Из этих уравнений находим соответственно:<br>1 2 х =(-1)"агсзш- + ял; х = ± агссоз(—)+2ял. <И]<br>3 5<br>Пример 6. Решить уравнение 2 зт х соз 5х - соз 5х=0. Решение. Имеем со85лс(28тл<;-1)=0. Значит, приходим к совокупности уравнений:<br>„ „ . 1 соз 5х = 0; 81П х=—.<br>2<br>„ я я тсп<br>Из первого уравнения находим :5х = — + я л, ж = —+ —.<br>я<br>Из второго уравнения находим: х =(-1)" — + ял.<br>6<br>Л я ял , „,„ я<br>Ответ: х=— + —; дс =(—1) — + ял. 10 5 ^ ' 6<br>Замечание. Учтите, что переход от уравнения ^(лс)-Ц(х)=0 к совокупности уравнений: ^(х)=0;^(х)=0 не всегда безопасен. Рассмотрим, например, уравнение х(зтх-1)=0. Из уравнения 1б*=0 находим<br>я<br>х = ял; из уравнения зтл: = 1 находим лс = —+ 2ял. Но включить обе серии<br>я<br>решений в ответ нельзя. Дело в том, что при значениях х = — + 2ял.входя-<br>94<br>щий в заданное уравнение множитель х не имеет смысла, т.е. значения<br>ж<br>х = — + 2пп не принадлежат области определения уравнения (области допустимых значений уравнения — ОДЗ), это — посторонние корни.<br>3. Однородные тригонометрические уравнения<br>Здесь мы познакомимся с довольно часто встречающимися на практике тригонометрическими уравнениями специального вида.<br>Определение. Уравнение вида: аз1пх + Ьсозх =0 называют однородным тригонометрическим уравнением первой степени; уравне-н ие вида: азю2 х + Ьз1п х соз х + с соз2 х = 0 называют однородным тригонометрическим уравнением второй степени.<br>Сначала поговорим о решении однородных тригонометрических уравнений первой степени, причем рассмотрим только самый общий случай, когда оба коэффициента а и Ъ отличны от нуля, так как, если а =0, уравнение принимает вид Ьсоз х=0, т.е. соз х=0 — такое уравнение отдельного обсуждения не заслуживает; аналогично при Ь=0 получаем зт х =0, что тоже не требует отдельного обсуждения.<br>Итак, дано уравнение азтх+Ьсозх=0, где а * 0,Ь * 0. Разделив обе части уравнения почленно на соз*, получим:<br>азтзс Ьсозх 0 , Л<br>-+-=-, т.е. а1%х+Ъ=0.<br>соз х соз х со&х<br>В итоге приходим к простейшему тригонометрическому уравнению<br>Ъ<br>= —. а<br>Внимание! Вообще-то делить обе части уравнения на одно и то же выражение можно только в том случае, когда мы уверены, что это выражение нигде не обращается в нуль (на 0 делить нельзя). Уверены ли мы, что в нашем уравнении соз х отличен от нуля? Давайте проанализируем. Предположим, что соз х =0. Тогда однородное уравнение а зтх+Ь соз х=0 примет вида зтдг=0, т.е. зщх=0 (вы ведь не забыли, что коэффициент а отличен от нуля). Получается, что и соз х=0, и зш л: =0, а это невозможно, так как зтх и соззс обращаются в нуль в различных точках. Итак, в однородном тригонометрическом уравнении первой степени деление обеих частей уравнения насозх— вполне благополучная операция.<br>Уравнения вида а зт тх+Ь соз тх=0 тоже называют однородными тригонометрическими уравнениями первой степени. Для их решения обе части уравнения делят почленно на соз тх.<br>Пример 7. Решить уравнение2 зт х-3соз х=0.<br>Решение. Разделив обе части уравнения почленно на соз х, получим:<br>95<br>3 3<br>21§лс-3=0, л: = —, лс = агс 1%- + пп.<br>2 2<br>3<br>Ответ: х = агс1е- + пп.<br>2<br>Пример 8. Решить уравнение 8т2лс + со82лс =0.<br>Решение. Разделив обе части уравнения почленно насо82лс, получим: 182*+ 1=0, 1&2х=-1, 2х = агс1ё(-1)+ пп,<br>„л п пп<br>2х = — + пп, х = — + —.<br>4 8 2<br>^ п пп<br>Ответ: х ----1--.<br>8 2_^<br>Рассмотрим теперь однородное тригонометрическое уравнение второй степени:<br>а 81П2 х+Ь 81П x соз Х+С соз2 X =0.<br>Если коэффициент а отличен от нуля, т.е. в уравнении содержится член зт2 х с каким-то коэффициентом, отличным от нуля, то, рассуждая как и выше, нетрудно убедиться в том, что при интересующих нас значениях переменной сое хне обращается в нуль, а потому можно обе части уравнения разделить почленно на сое2 х. Что это даст? Смотрите:<br>а 81п2 X Ь 81п X соз X С соз2 X 0<br>сов2 X соз2 X сов2 X соз2 X<br>т.е. а 1§2х+Ь х+с =0.<br>Это — квадратное уравнение относительно новой переменной г = 1%х.<br>Пусть теперь в однородном тригонометрическом уравнении<br>а 81п2 Х + Ь 81п X соз Х + С соз2 X =0<br>коэффициент а равен 0, т.е. отсутствует член азт2 х. Тогда уравнение принимает вид:<br>Ь 81п X соз х + ссоз2 Х = 0.<br>Это уравнение можно решить методом разложения на множители: с08 X (Ъ 81п Х + С соз X) =0, соз X = 0 или Ъ 81п Х + С соз X =0.<br>Получились два уравнения, которые мы с вами решать умеем. Аналогично обстоит дело и в случае, когдас =0, т.е. когда однородное уравнение имеет вид а зт2 х+Ь зт х соз х=0 (здесь можно вынести за скобки зтх).<br>Фактически мы выработали<br>96<br>АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЯ автгх+Ь 81П хсоз х+ссоа2 х=0:<br>1. Посмотреть, есть ли в уравнении член азт2 х.<br>2. Если членавт2 хв уравнении содержится (т.е. а Ф 0), то уравнение решается делением обеих его частей на сое2 х и последующим введением новой переменной г = х.<br>3. Если член азт2 х в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят совх.<br>Так же обстоит дело и в однородных уравнениях вида: а 81П2 тх+Ъ 8111 тхсовтх+с сов2 тх=0.<br>Пример 9. Решить уравнение<br>81П2 лс - 3 81П л: соз х+ 2 сое2 х = 0.<br>Решение. Разделив обе част^ уравнения почленно на соз2 х, получим 1^х-31§ х + 2=0. Введя новую переменную г=Щх, получим г2 -Зг + 2=0, откуда находим г1 = 1, г2 =2. Значит, либо {%х = 1, либо 1%х=2. Из первого уравнения находим:<br>х = агс1ё 1 + пп, т.е. х = — + пп.<br>Из второго уравнения находим: х = агс1§ 2 + пп. п<br>Ответ: х = — + пп\ х = агс1§ 2 + пп. 4<br>Пример 10. Решить уравнение<br>•у/Ззтлссовлс + соз2 х=0.<br>Решение. Здесь отсутствует член вида а зш2 х, значит, делить обе части уравнения на соз2 х нельзя. Решим уравнение методом разложения на множители. Имеем:<br>совх(4з 8Н1л; + со8л;)=0, т.е. соз х = 0 или 73 зш х + соз х=0.<br>тт я<br>Из первого уравнения находим х = — + кп.<br>Второе уравнение — однородное тригонометрическое уравнение первой степени. Решим его с помощью почленного деления обеих частей уравнения насозлс:<br>81пя; + Со8я;=0,<br>4З^х + 1=0;<br>-П п<br>—Г= + пп,х = — + пп. л/3 6<br>1е л: = —Дг, откуда х = агс1§<br>4з<br>Ответ: х = — + пп: х = -—+пп. 2 6<br>В заключение рассмотрим более сложный пример.<br>4 Мордкович «Алгебра, 10 кл.»<br>97<br>Пример 11. Решить уравнение<br>3 81 п2 Зле - 2л/3 81Г1 Зх сое Зле + 5 сое2 Зле = 2 и выделить те его корни, которые принадлежат интервалу (-л, л).<br>Решение. Чем это уравнение сложнее предыдущих? Во-первых, оно не является однородным, так как в правой его части содержится не 0, а 2. Во-вторых, в левой части уравнения под знаками синуса и косинуса находится не х, а Зле. В-третьих, нужно не только решить уравнение в общем виде, но и выбрать корни, принадлежащие заданному промежутку. Эти три дополнительные трудности мы сейчас и начнем преодолевать.<br>С числом 2, содержащимся в правой части уравнения, мы поступим следующим образом. Известно, что зт21 + сое21 = 1 — это тождество верно для любого I. В частности, зт2 3* + сое2 Зле = 1. Но тогда 2 зт2 Зх + 2соз2 Зх =2. Заменив в правой части уравнения 2 на 2 81п2 Зле + 2со82 Зле, получим:<br>3 зт2 Зх - 273 зт Зх соа Зх + 5 соз2 Зх=2зт2Зх + 2 сов2 Зх.<br>Далее имеем:<br>3 зт2 Зх -2-Уз зт Зх соз Зх + 5сое2 3*'-2 зт2 Зх-2сов2 Зле = О, зт2 Зх-2^3 зт Зх соз Зле + Зсоз2 Зле =0.<br>Как видите, нам удалось преобразовать заданное уравнение в однородное тригонометрическое уравнение второй степени. Оно содержит в своем составе член зт2 Зх, значит, применив способ почленного деления на соз2 Зле, получим:<br>1§2 3 лс - 2-У31§ Зле + 3=0.<br>Положив г Зх, получим квадратное уравнение:<br>г2 -2л/3г +3=0.<br>Для решения этого уравнения можно использовать формулу корней квадратного уравнения, но изящнее сделать так: заметив, что<br>г2 -273г+3=(г-73)2, преобразовать квадратное уравнение к виду:<br>(г-7з)2=0,<br>и далее г--Уз =0.<br>Значит, 2 = л/5, т.е.<br>1§ЗХ = ТЗ, Зх = ап*8 -Уз + пп,<br>о 71<br>Злс = — + пп, 3<br>л пп<br>лс = - +-.<br>9 3<br>Осталось из найденной серии решений выбрать те корни уравнения, которые принадлежат заданному интервалу (-л, л). Можно осуществить «перебор по параметру», т.е. последовательно придать параметру п значения 0,1, 2,..., -1, -2,..., как мы это делали в п. 1 (примеры 2 иЗ). Но мы хотим показать вам еще один прием (быть может, он покажется вам более интересным).<br>98<br>Нам нужно найти такие значения х, которые содержатся в интервале (-л, л), т.е. удовлетворяют двойному неравенству -%<х<к. Поскольку л лл<br>х =— + —, получаем неравенство:<br>П ПП -л< —+-< л.<br>9 3<br>Умножив все части этого неравенства на 9 и разделив на тс, получим:<br>-9<1 + Зл<9, -10<3я<8,<br>10 8<br>--<п <-.<br>3 3<br>Осталось выяснить, какие целочисленные значения параметра п удовлетворяют последнему неравенству. Это значения: -3, -2, -1, 0,1, 2. Значит, если перечисленные шесть значений подставить вместо п в форте тел<br>мулу решении х = — н--, то мы тем самым и выделим интересующие нас<br>9 3<br>корни уравнения, принадлежащие заданному интервалу (-тс, тс). Итак:<br>1) если л = -3, то из формулы х=— + — получаем<br>9 3<br>п 8л<br>х =--л=--;<br>9 9<br>2) если л = -2, то из формулы х = — + — получаем<br>9 3<br>л _ 2л __ 5 л<br>3) если л = -1, то из формулы х + ^ получаем<br>_ л _ л _ 2 л<br>4) если л = 0, то из формулы + ~ получаем<br>л „ л<br>х=- + 0=~; 9 9<br>С\ 1 Я тел<br>5) если л = I, то из формулы х=—л--получаем<br>9 3 _ л я_4тс. *"9 + 3~~9~'<br>6) если л = 2, то из формулы х=— + — получаем<br>9 3<br>п 2тс 7тс<br>х=- +-=-.<br>9 3 9<br>^ 8л 5 л 2 л п 4тс 7п<br>Ответ:--;--;--; —; —.<br>9 9 9 9 9 9<br>4 й<br>99<br>
| + | <br>[[Image:Alga332.jpg|550px|Решение уравнения]] |
| | | | |
| - | А.Г. Мордкович Алгебра 10 класс
| + | Во всех перечисленных формулах подразумевается, что параметр (n, к и т.д.) принимает любые целочисленные значения [[Image:Alga333.jpg]]<br> |
| | | | |
| - | <br>
| + | Во всех этих формулах, которые перечислены выше, следует понимать, что параметр (n, к и т.д.) может принимать любые целочисленные значения. |
| | | | |
| - | <sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub>
| + | Также к простейшим уравнениям можно отнести и такие уравнения, которые имеют вид: |
| | + | Т(кх + m)=а. В этом случае Т является знаком какой-нибудь тригонометрической функции. А теперь давайте попробуем это рассмотреть на примере решения уравнения. |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | '''Пример 1.''' Нам нужно решить данные уравнения: |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | |
| - |
| + | |
| - | '''<u>Практика</u>'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | |
| - |
| + | |
| - | '''<u>Дополнения</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| - |
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| - | <br>
| + | [[Image:Alga334.jpg|320px|Задание]] |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | '''Решение:''' |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | а) Для решения этого уравнения нам понадобиться в первую очередь ввести новую переменную: |
| | + | |
| | + | [[Image:Alga335.jpg|690px|Решение]] |
| | + | |
| | + | Далее, мы вернемся к переменной х, и соответственно получим: |
| | + | |
| | + | [[Image:Alga336.jpg|120px|Формула]] |
| | + | |
| | + | Теперь нам остается разделить почленно на два обе эти части, в итоге мы получим: |
| | + | |
| | + | [[Image:Alga337.jpg|120px|Формула]]<br> |
| | + | |
| | + | Но здесь обратите внимание на то, что приобретя некоторый опыт решения таких уравнений, появляется возможность без ввода промежуточной переменной t = 2х, сразу переходить от уравнения |
| | + | |
| | + | <br>[[Image:Alga338.jpg|320px|Уравнения]] |
| | + | |
| | + | Таким методом мы постараемся действовать и в дальнейшем. |
| | + | |
| | + | б) Нам с вами уже известно, что при решении такого уравнения, как соs t = а, оно приобретает вид: |
| | + | |
| | + | [[Image:Alga339.jpg|180px|Уравнение]] |
| | + | |
| | + | А это будет означать, что: |
| | + | |
| | + | [[Image:Alga340.jpg|690px|Задание]]<br> |
| | + | |
| | + | Рассмотрим второй пример. |
| | + | |
| | + | '''Пример 2.''' Нам необходимо найти корни такого уравнения, как: |
| | + | |
| | + | <br>[[Image:Alga341.jpg|Уравнение]] |
| | + | |
| | + | Эти корни принадлежат отрезку[0, п]. |
| | + | Приступим к решению. |
| | + | |
| | + | '''Решение.''' |
| | + | |
| | + | Внвчале мы с вами решим это уравнение в общем виде, руководствуясь примером 1а: |
| | + | |
| | + | [[Image:Alga342.jpg|120px|Уравнение]] |
| | + | |
| | + | Теперь попробуем последовательно придать параметру п, такие значения, как: 0,1, 2,..., -1, -2,... , а далее возьмем и подставим эти значения в общую формулу корней. |
| | + | Смотрим, что у нас вышло: |
| | + | |
| | + | [[Image:Alga343.jpg|550px|Задание]] |
| | + | |
| | + | А получилось у нас то, что данное число не принадлежит заданному отрезку [0, п], также как и не принадлежать заданному отрезку и все те значения х, которые мы получили из общей формулы при n = -2, -3,... |
| | + | Сейчас внимательно посмотрите на рис. 94. На нем мы видим геометрическую интерпретацию проведенных рассуждений.<br> |
| | + | |
| | + | <br>[[Image:Alga344.jpg|320px|Задание]]<br> |
| | + | |
| | + | Решив уравнение и рассмотрев рисунок, мы с вами пришли к выводу, что заданному отрезку [0, п] могут принадлежать корни уравнения, полученные из общей формулы, если параметр n имеет следующие значения: n = 0, n = 1. |
| | + | |
| | + | Вот как выглядят эти корни: |
| | + | |
| | + | [[Image:Alga345.jpg]] |
| | + | |
| | + | Следовательно, мы получаем такой ответ: |
| | + | |
| | + | [[Image:Alga345.jpg]] |
| | + | |
| | + | Перейдем к решению следующего примера. |
| | + | |
| | + | '''Пример 3.''' Дано уравнение |
| | + | |
| | + | [[Image:Alga346.jpg|120px|Формула]]<br> |
| | + | |
| | + | и нам нужно найти корни, принадлежащие отрезку |
| | + | |
| | + | [[Image:Alga347.jpg]]<br> |
| | + | |
| | + | Решение: В первую очередь нам нужно решить это уравнение в общем виде, взяв за пример решения задание 1б: |
| | + | |
| | + | [[Image:Alga348.jpg|120px|Формула]] |
| | + | |
| | + | Далее необходимо придать последовательно параметру n, значения 0,1, 2,..., -1, -2,... |
| | + | Следующим нашим шагом нужно будет подставить все эти значения в общую формулу корней. |
| | + | Смотрим, вот что у нас вышло: |
| | + | |
| | + | <br>[[Image:Alga349.jpg|550px|Задание]] |
| | + | |
| | + | У нас получились числа, которые больше числа n. И мы снова приходим к выводу, что значения х, которые мы получили из общей формулы при n = 3,4,..., тем более не могут принадлежать заданному отрезку. |
| | + | |
| | + | [[Image:Alga350.jpg|550px|Задание]] |
| | + | |
| | + | Так же, как и не могут принадлежать отрезку значения х, полученные из общей формулы, если n = -2, - 3,... |
| | + | |
| | + | Рассмотрите внимательно представленную на рис. 95 интерпретацию проведенных рассуждений. |
| | + | |
| | + | [[Image:Alga351.jpg|320px|Задание]] |
| | + | |
| | + | Из этого следует, что заданному отрезку |
| | + | |
| | + | [[Image:Alga352.jpg]] |
| | + | |
| | + | принадлежат такие корни уравнения, как: |
| | + | |
| | + | [[Image:Alga353.jpg|240px|Задание]] |
| | + | |
| | + | <h2>Два основных метода решения тригонометрических уравнений</h2> |
| | + | |
| | + | А сейчас мы с вами перейдем к рассмотрению основных методов решения тригонометрических уравнений. Для этих целей, как правило, используют: |
| | + | |
| | + | • во-первых, метод введения новой переменной;<br> |
| | + | • во-вторых, способ разложения на множители.<br> |
| | + | |
| | + | А сейчас давайте вернемся немного назад и вспомним, как на третьем примере мы с вами решили тригонометрическое уравнение: |
| | + | |
| | + | [[Image:Alga354.jpg|120px|Задание]] |
| | + | |
| | + | Вспомним, что мы сделали в первую очередь. Во-первых, ввели новую переменную ю z = sin t, а потом переписали уравнение, которое приобрело такой вид:<br> |
| | + | |
| | + | [[Image:Alga355.jpg|240px|Задание]] |
| | + | |
| | + | В итоге, мы с вами получили два простых уравнения: |
| | + | |
| | + | [[Image:Alga356.jpg|120px|Задание]] |
| | + | |
| | + | Из сделанных ранее выводов мы увидели, что первое уравнение не имеет решения. А вот второе имеет их целых два: |
| | + | |
| | + | [[Image:Alga357.jpg|120px|Задание]] |
| | + | |
| | + | Далее мы увидели, что их можно объединить одной формулой |
| | + | |
| | + | [[Image:Alga358.jpg|120px|Задание]] |
| | + | |
| | + | Вспомните, как было решено это тригонометрическое уравнение: |
| | + | |
| | + | [[Image:Alga359.jpg|480px|Задание]] |
| | + | |
| | + | '''Пример 4.''' Решим следующее уравнение. |
| | + | |
| | + | [[Image:Alga360.jpg|120px|Задание]] |
| | + | |
| | + | '''Решение.''' |
| | + | |
| | + | Возьмем уравнение: |
| | + | |
| | + | [[Image:Alga361.jpg|80px|Задание]] |
| | + | |
| | + | Попробуем в него ввести новую переменную: |
| | + | |
| | + | [[Image:Alga362.jpg|80px|Задание]] |
| | + | |
| | + | Смотрим, что это нам даст. А это нам позволит записать уравнение, которое имеет более простой вид: |
| | + | |
| | + | [[Image:Alga363.jpg|80px|Задание]] |
| | + | |
| | + | Смотрим, что мы имеем: |
| | + | |
| | + | [[Image:Alga364.jpg|120px|Задание]] |
| | + | |
| | + | Теперь вернемся к переменной х, ну и в итоге получим уже два уравнения: |
| | + | |
| | + | <br>[[Image:Alga365.jpg|550px|Задание]] |
| | + | |
| | + | С методом введения новой переменной мы уже выяснили, а сейчас попробуем решить тригонометрическое уравнение вторым способом, методом разложения на множители. |
| | + | В принципе, с этим методом вы также знакомы. |
| | + | |
| | + | Берем уравнение f(х) =0 и пробуем преобразовать его к такому виду: |
| | + | |
| | + | [[Image:Alga366.jpg]] |
| | + | |
| | + | Для этого нам нужно решить два уравнения: |
| | + | |
| | + | [[Image:Alga367.jpg]] |
| | + | |
| | + | '''Пример 5.''' В следующем примере решение задачи также сводится к решению совокупности уравнений |
| | + | |
| | + | '''Решение.''' |
| | + | |
| | + | [[Image:Alga368.jpg|180px|Задание]] |
| | + | |
| | + | И соответственно из этих уравнений у нас выходит: |
| | + | |
| | + | [[Image:Alga369.jpg|180px|Задание]] |
| | + | |
| | + | [[Image:Alga370.jpg|320px|Задание]] |
| | + | |
| | + | '''Пример 6.''' Следующее уравнение решаем по такому же принципу. |
| | + | |
| | + | [[Image:Alga371.jpg|240px|Задание]] |
| | + | |
| | + | '''Решение.''' |
| | + | |
| | + | Нам дано следующее уравнение: |
| | + | |
| | + | <br>[[Image:Alga372.jpg|180px|Задание]] |
| | + | |
| | + | Следовательно, приходим к совокупности уравнений: |
| | + | |
| | + | [[Image:Alga373.jpg|550px|Задание]] |
| | + | |
| | + | Замечание. Тут необходимо учесть то, что не всегда переход от уравнения: |
| | + | |
| | + | [[Image:Alga374.jpg|120px|Задание]] |
| | + | |
| | + | к совокупности уравнений: |
| | + | |
| | + | <br>[[Image:Alga375.jpg|120px|Задание]] |
| | + | |
| | + | Является безопасным. |
| | + | |
| | + | Например, берем уравнение: |
| | + | |
| | + | [[Image:Alga376.jpg|120px|Задание]] |
| | + | |
| | + | С помощью уравнения tg x = 0 находим х = пn, а из уравнения sin x = 1 находим |
| | + | |
| | + | [[Image:Alga377.jpg|80px|Формула]] |
| | + | |
| | + | Но здесь присутствует одно «но», так как включить обе серии решений в ответ нельзя. |
| | + | |
| | + | Так как при значении |
| | + | |
| | + | <br>[[Image:Alga377.jpg|80px|Формула]] |
| | + | |
| | + | Его множитель tg х не имеет смысла, другими словами он не имеет значения, так как не является областью определения уравнения, т.е. – это посторонние корни. |
| | + | |
| | + | <br>[[Image:Alga377.jpg|80px|Формула] |
| | + | |
| | + | <h2>Однородные тригонометрические уравнения</h2> |
| | + | |
| | + | Теперь давайте рассмотрим и тригонометрические уравнения, которые имеют специальный вид, но встречаются довольно таки часто. |
| | + | |
| | + | '''Определение.''' Уравнение, имеющее вид: |
| | + | |
| | + | [[Image:Alga378.jpg|120px|Формула]] |
| | + | |
| | + | называется однородным тригонометрическим уравнением 1-й степени; |
| | + | а уравнение, которое выглядит так: |
| | + | |
| | + | <br>[[Image:Alga379.jpg|240px|Формула]] |
| | + | |
| | + | является однородным тригонометрическим уравнением 2-й степени. |
| | + | |
| | + | '''Уравнения 1-й степени''' |
| | + | |
| | + | Давайте рассмотрим общий случай решения тригонометрических уравнений, в котором коэффициенты а и b отличны от нуля, ведь при а =0, уравнение будет иметь вид |
| | + | |
| | + | [[Image:Alga380.jpg|180px|Задание]] |
| | + | |
| | + | а такое уравнение мы обсуждать не будем, так же, как и |
| | + | при b=0 получаем sin х =0. |
| | + | |
| | + | Нам дано уравнение: |
| | + | |
| | + | [[Image:Alga381.jpg|240px|Задание]] |
| | + | |
| | + | Делим его части почленно на соs x, и получим: |
| | + | |
| | + | [[Image:Alga382.jpg|320px|Задание]] |
| | + | |
| | + | Вот мы и пришли к простейшему тригонометрическому уравнению |
| | + | |
| | + | [[Image:Alga383.jpg|120px|Формула]] |
| | + | |
| | + | Внимание! Следует запомнить, что делить обе части уравнения на одно и то же выражение можно только в случае, если это выражение нигде не обращается в нуль. А вот как в этом убедиться? |
| | + | |
| | + | '''Пример 7.''' Давайте решим уравнение 2 sin х - 3соs х = 0. |
| | + | |
| | + | Решение. Разделим почленно на соs х, обе части уравнения и у нас получится: |
| | + | |
| | + | [[Image:Alga384.jpg|240px|Задание]] |
| | + | |
| | + | Пример 8. Дано уравнение 2x + соs2x =0. |
| | + | Решение. Разделим почленно на соs 2 x обе части уравнения и получим: |
| | + | |
| | + | [[Image:Alga385.jpg|320px|Задание]] |
| | + | |
| | + | Теперь приступим к однородному тригонометрическому уравнению 2-й степени: |
| | + | |
| | + | [[Image:Alga386.jpg|240px|Формула]] |
| | + | |
| | + | Если в данном уравнении содержится член sin 2 х, у которого коэффициент отличный от 0, то при интересующих нас значениях переменной соs х не обращается в нуль, и следовательно обе части уравнения можно разделить почленно на соs 2 х. И вот что мы получим: |
| | + | |
| | + | <br>[[Image:Alga387.jpg|320px|Задание]] |
| | + | |
| | + | А получили мы квадратное уравнение относительно новой переменной z = tg х. |
| | + | Если в однородном тригонометрическом уравнении: |
| | + | |
| | + | [[Image:Alga388.jpg|240px|Задание]] |
| | + | |
| | + | коэффициент а = 0, т.е. отсутствует член sin2 х. Тогда мы получим такое уравнение: |
| | + | |
| | + | [[Image:Alga389.jpg|240px|Задание]] |
| | + | |
| | + | И решаем его методом разложения на множители: |
| | + | |
| | + | [[Image:Alga390.jpg|240px|Задание]] |
| | + | |
| | + | У нас получается два уравнения. Также обстоит дело, когда с = 0, т.е. когда однородное уравнение имеет вид, где sin х можно вынести за скобки. |
| | + | |
| | + | Фактически мы с вами получили |
| | + | |
| | + | [[Image:Alga392.jpg|480px|Алгоритм решения уравнения]]<br> |
| | + | |
| | + | ''А.Г. Мордкович Алгебра 10 класс'' |
Текущая версия на 07:23, 25 июня 2015
Гипермаркет знаний>>Математика>>Математика 10 класс>> Тригонометрические уравнения
§ 20. Тригонометрические уравнения
Простейшие тригонометрические уравнения
Все уравнения, которые содержат переменную под знаком тригонометрических функций, называются тригонометрическим уравнением. Если перед вами уравнения такого вида, как:
sin x = a; cos x = a; tg x = a; ctg x = a,
в котором x является его переменной, и a является действительным числом, то такие уравнения называются простейшими тригонометрическими уравнениями.
И если нам с вами известно, что в том случае, когда:
1) | а | < 1, то решения уравнения cos о:-а приобретает такой вот вид:

Во всех перечисленных формулах подразумевается, что параметр (n, к и т.д.) принимает любые целочисленные значения 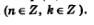
Во всех этих формулах, которые перечислены выше, следует понимать, что параметр (n, к и т.д.) может принимать любые целочисленные значения.
Также к простейшим уравнениям можно отнести и такие уравнения, которые имеют вид:
Т(кх + m)=а. В этом случае Т является знаком какой-нибудь тригонометрической функции. А теперь давайте попробуем это рассмотреть на примере решения уравнения.
Пример 1. Нам нужно решить данные уравнения:
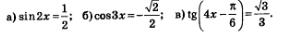
Решение:
а) Для решения этого уравнения нам понадобиться в первую очередь ввести новую переменную:
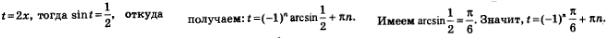
Далее, мы вернемся к переменной х, и соответственно получим:
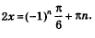
Теперь нам остается разделить почленно на два обе эти части, в итоге мы получим:
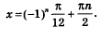
Но здесь обратите внимание на то, что приобретя некоторый опыт решения таких уравнений, появляется возможность без ввода промежуточной переменной t = 2х, сразу переходить от уравнения

Таким методом мы постараемся действовать и в дальнейшем.
б) Нам с вами уже известно, что при решении такого уравнения, как соs t = а, оно приобретает вид:

А это будет означать, что:

Рассмотрим второй пример.
Пример 2. Нам необходимо найти корни такого уравнения, как:
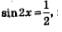
Эти корни принадлежат отрезку[0, п].
Приступим к решению.
Решение.
Внвчале мы с вами решим это уравнение в общем виде, руководствуясь примером 1а:
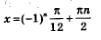
Теперь попробуем последовательно придать параметру п, такие значения, как: 0,1, 2,..., -1, -2,... , а далее возьмем и подставим эти значения в общую формулу корней.
Смотрим, что у нас вышло:

А получилось у нас то, что данное число не принадлежит заданному отрезку [0, п], также как и не принадлежать заданному отрезку и все те значения х, которые мы получили из общей формулы при n = -2, -3,...
Сейчас внимательно посмотрите на рис. 94. На нем мы видим геометрическую интерпретацию проведенных рассуждений.
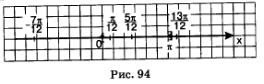
Решив уравнение и рассмотрев рисунок, мы с вами пришли к выводу, что заданному отрезку [0, п] могут принадлежать корни уравнения, полученные из общей формулы, если параметр n имеет следующие значения: n = 0, n = 1.
Вот как выглядят эти корни:
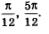
Следовательно, мы получаем такой ответ:
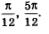
Перейдем к решению следующего примера.
Пример 3. Дано уравнение
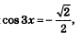
и нам нужно найти корни, принадлежащие отрезку
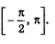
Решение: В первую очередь нам нужно решить это уравнение в общем виде, взяв за пример решения задание 1б:
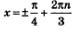
Далее необходимо придать последовательно параметру n, значения 0,1, 2,..., -1, -2,...
Следующим нашим шагом нужно будет подставить все эти значения в общую формулу корней.
Смотрим, вот что у нас вышло:

У нас получились числа, которые больше числа n. И мы снова приходим к выводу, что значения х, которые мы получили из общей формулы при n = 3,4,..., тем более не могут принадлежать заданному отрезку.
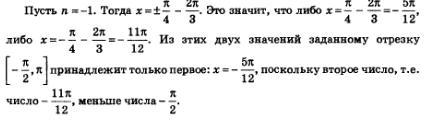
Так же, как и не могут принадлежать отрезку значения х, полученные из общей формулы, если n = -2, - 3,...
Рассмотрите внимательно представленную на рис. 95 интерпретацию проведенных рассуждений.
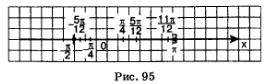
Из этого следует, что заданному отрезку
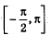
принадлежат такие корни уравнения, как:
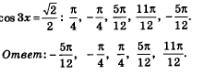
Два основных метода решения тригонометрических уравнений
А сейчас мы с вами перейдем к рассмотрению основных методов решения тригонометрических уравнений. Для этих целей, как правило, используют:
• во-первых, метод введения новой переменной;
• во-вторых, способ разложения на множители.
А сейчас давайте вернемся немного назад и вспомним, как на третьем примере мы с вами решили тригонометрическое уравнение:
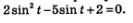
Вспомним, что мы сделали в первую очередь. Во-первых, ввели новую переменную ю z = sin t, а потом переписали уравнение, которое приобрело такой вид:
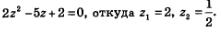
В итоге, мы с вами получили два простых уравнения:
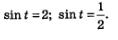
Из сделанных ранее выводов мы увидели, что первое уравнение не имеет решения. А вот второе имеет их целых два:
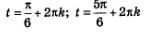
Далее мы увидели, что их можно объединить одной формулой
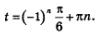
Вспомните, как было решено это тригонометрическое уравнение:
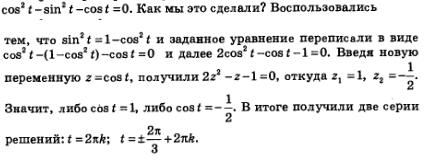
Пример 4. Решим следующее уравнение.
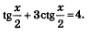
Решение.
Возьмем уравнение:
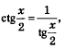
Попробуем в него ввести новую переменную:
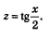
Смотрим, что это нам даст. А это нам позволит записать уравнение, которое имеет более простой вид:
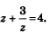
Смотрим, что мы имеем:
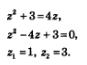
Теперь вернемся к переменной х, ну и в итоге получим уже два уравнения:

С методом введения новой переменной мы уже выяснили, а сейчас попробуем решить тригонометрическое уравнение вторым способом, методом разложения на множители.
В принципе, с этим методом вы также знакомы.
Берем уравнение f(х) =0 и пробуем преобразовать его к такому виду:
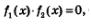
Для этого нам нужно решить два уравнения:
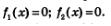
Пример 5. В следующем примере решение задачи также сводится к решению совокупности уравнений
Решение.
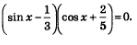
И соответственно из этих уравнений у нас выходит:
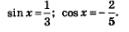
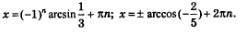
Пример 6. Следующее уравнение решаем по такому же принципу.
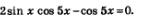
Решение.
Нам дано следующее уравнение:
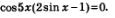
Следовательно, приходим к совокупности уравнений:
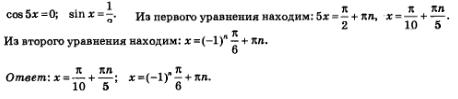
Замечание. Тут необходимо учесть то, что не всегда переход от уравнения:
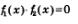
к совокупности уравнений:
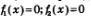
Является безопасным.
Например, берем уравнение:
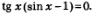
С помощью уравнения tg x = 0 находим х = пn, а из уравнения sin x = 1 находим
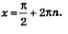
Но здесь присутствует одно «но», так как включить обе серии решений в ответ нельзя.
Так как при значении
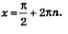
Его множитель tg х не имеет смысла, другими словами он не имеет значения, так как не является областью определения уравнения, т.е. – это посторонние корни.
[[Image:Alga377.jpg|80px|Формула]
Однородные тригонометрические уравнения
Теперь давайте рассмотрим и тригонометрические уравнения, которые имеют специальный вид, но встречаются довольно таки часто.
Определение. Уравнение, имеющее вид:
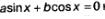
называется однородным тригонометрическим уравнением 1-й степени;
а уравнение, которое выглядит так:
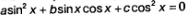
является однородным тригонометрическим уравнением 2-й степени.
Уравнения 1-й степени
Давайте рассмотрим общий случай решения тригонометрических уравнений, в котором коэффициенты а и b отличны от нуля, ведь при а =0, уравнение будет иметь вид
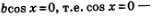
а такое уравнение мы обсуждать не будем, так же, как и
при b=0 получаем sin х =0.
Нам дано уравнение:
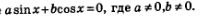
Делим его части почленно на соs x, и получим:
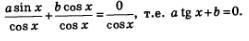
Вот мы и пришли к простейшему тригонометрическому уравнению
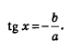
Внимание! Следует запомнить, что делить обе части уравнения на одно и то же выражение можно только в случае, если это выражение нигде не обращается в нуль. А вот как в этом убедиться?
Пример 7. Давайте решим уравнение 2 sin х - 3соs х = 0.
Решение. Разделим почленно на соs х, обе части уравнения и у нас получится:
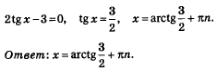
Пример 8. Дано уравнение 2x + соs2x =0.
Решение. Разделим почленно на соs 2 x обе части уравнения и получим:
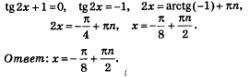
Теперь приступим к однородному тригонометрическому уравнению 2-й степени:

Если в данном уравнении содержится член sin 2 х, у которого коэффициент отличный от 0, то при интересующих нас значениях переменной соs х не обращается в нуль, и следовательно обе части уравнения можно разделить почленно на соs 2 х. И вот что мы получим:
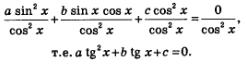
А получили мы квадратное уравнение относительно новой переменной z = tg х.
Если в однородном тригонометрическом уравнении:
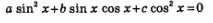
коэффициент а = 0, т.е. отсутствует член sin2 х. Тогда мы получим такое уравнение:
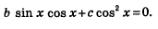
И решаем его методом разложения на множители:
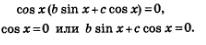
У нас получается два уравнения. Также обстоит дело, когда с = 0, т.е. когда однородное уравнение имеет вид, где sin х можно вынести за скобки.
Фактически мы с вами получили

А.Г. Мордкович Алгебра 10 класс
|