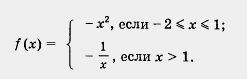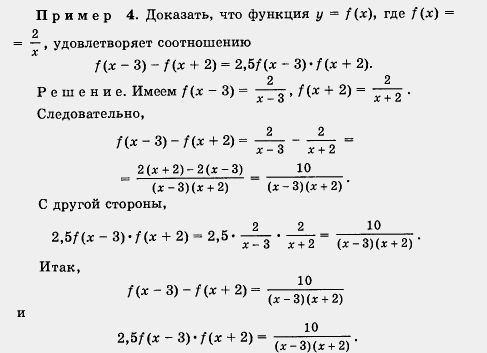|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Функция у = k/x, ее свойства и график
Функция у = k/x, ее свойства и график
В этом параграфе мы познакомимся с новой функцией — функцией 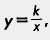 Коэффициент k может принимать любые значения, кроме k = 0. Рассмотрим сначала случай, когда k = 1; таким образом, сначала речь пойдет о функции Коэффициент k может принимать любые значения, кроме k = 0. Рассмотрим сначала случай, когда k = 1; таким образом, сначала речь пойдет о функции 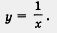 . .
Чтобы построить график функции 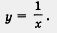 , поступим так же, как и в предыдущем параграфе: дадим независимой переменной х несколько конкретных значений и вычислим (по формулe , поступим так же, как и в предыдущем параграфе: дадим независимой переменной х несколько конкретных значений и вычислим (по формулe 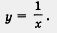 ) соответствующие значения зависимой переменной у. Правда, на этот раз удобнее проводить вычисления и построения постепенно, сначала придавая аргументу только положительные значения, а затем — только отрицательные. ) соответствующие значения зависимой переменной у. Правда, на этот раз удобнее проводить вычисления и построения постепенно, сначала придавая аргументу только положительные значения, а затем — только отрицательные.
Первый этап. Если х = 1, то у = 1 (напомним, что мы пользуемся формулой 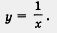 ); );

Короче говоря, мы составили следующую таблицу:
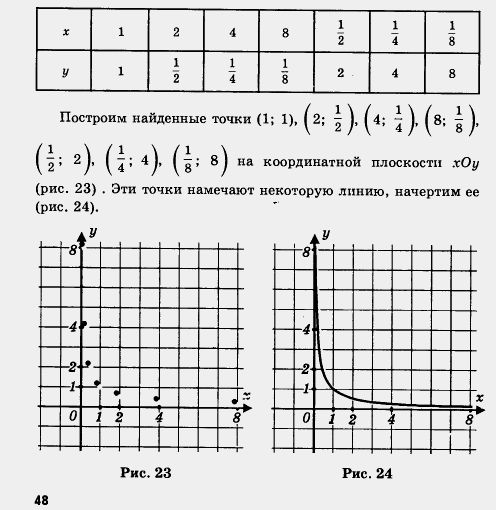
Второй этап.

Короче говоря, мы составили следующую таблицу:
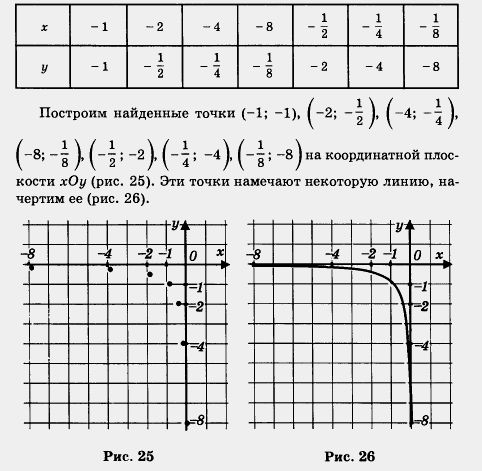
А теперь объединим два этапа в один, т. е. из двух рисунков 24 и 26 сделаем один (рис. 27). Это и есть график функции 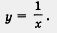 его называют гиперболой. его называют гиперболой.
Попробуем по чертежу описать геометрические свойства гиперболы.
Во-первых, замечаем, что эта линия выглядит так же красиво, как парабола, поскольку обладает симметрией. Любая прямая, проходящая через начало координат О и расположенная в первом и третьем координатных углах, пересекает гиперболу в двух точках, которые лежат на этой прямой по разные стороны от точки О, но на равных расстояниях от нее (рис. 28). Это присуще, в частности, точкам (1; 1) и (- 1; - 1),
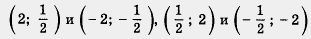 и т. д.Значит - О центр симметрии гиперболы. Говорят также, что гипербола симметрична относительно начала координат. и т. д.Значит - О центр симметрии гиперболы. Говорят также, что гипербола симметрична относительно начала координат.
Во-вторых, видим, что гипербола состоит из двух симметричных относительно начала координат частей; их обычно называют ветвями гиперболы.
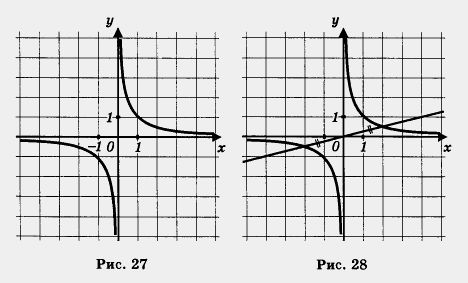
В-третьих, замечаем, что каждая ветвь гиперболы в одном направлении подходит все ближе и ближе к оси абсцисс, а в другом направлении — к оси ординат. В подобных случаях соответствующие прямые называют асимптотами.
Значит, график функции 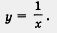 , т.е. гипербола, имеет две асимптоты: ось х и ось у. , т.е. гипербола, имеет две асимптоты: ось х и ось у.
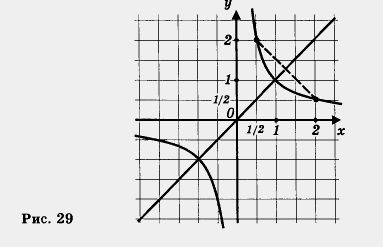
Если внимательно проанализировать построенный график, то можно обнаружить еще одно геометрическое свойство, не такое очевидное, как три предыдущих (математики обычно говорят так: «более тонкое свойство»). У гиперболы имеется не только центр симметрии, но и оси симметрии.
В самом деле, построим прямую у = х (рис. 29). А теперь смотрите: точки 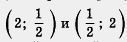 расположены по разные стороны от проведенной прямой, но на равных расстояниях от нее. Они симметричны, относительно этой прямой. Тоже можно сказать о точках расположены по разные стороны от проведенной прямой, но на равных расстояниях от нее. Они симметричны, относительно этой прямой. Тоже можно сказать о точках 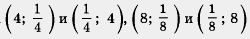 , где, конечно , где, конечно 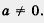 Значит, прямая y =x - ось симетрии гиперболы Значит, прямая y =x - ось симетрии гиперболы 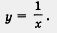 ( равно как и y = -x) ( равно как и y = -x)
Пример 1. Найти наименьшее и наибольшее значения функции 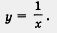 а) на отрезке а) на отрезке 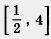 ; б) на отрезке [- 8, - 1]. ; б) на отрезке [- 8, - 1].
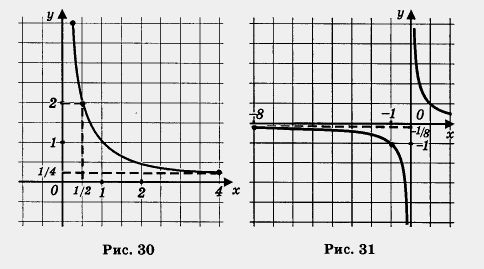
Решение, а) Построим график функции 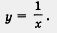 и выделим ту его часть, которая соответствует значениям переменной х из отрезка и выделим ту его часть, которая соответствует значениям переменной х из отрезка 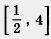 (рис. 30). Для выделенной части графика находим: (рис. 30). Для выделенной части графика находим:
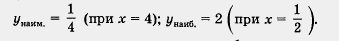
б) Построим график функции 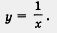 и выделим ту его часть, которая соответствует значениям переменной х из отрезка [- 8, - 1] (рис. 31). Для выделенной части графика находим: и выделим ту его часть, которая соответствует значениям переменной х из отрезка [- 8, - 1] (рис. 31). Для выделенной части графика находим:
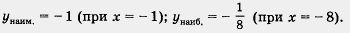
Итак, мы рассмотрели функцию 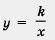 для случая, когда k= 1. Пусть теперь k — положительное число, отличное от 1, например k = 2. для случая, когда k= 1. Пусть теперь k — положительное число, отличное от 1, например k = 2.
Рассмотрим функцию 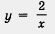 и составим таблицу значений этой функции: и составим таблицу значений этой функции:

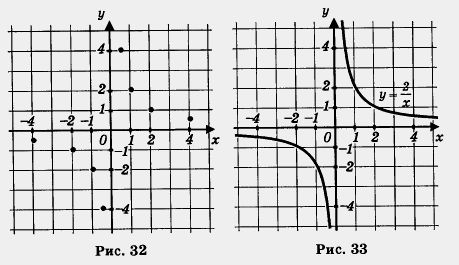
Построим точки (1; 2), (2; 1), (-1; -2), (-2; -1), 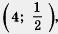 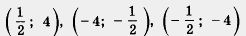
на координатной плоскости (рис. 32). Они намечают некоторую линию, состоящую из двух ветвей; проведем ее (рис. 33). Как и график функции 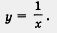 , эту линию называют гиперболой. , эту линию называют гиперболой.
Рассмотрим теперь случай, когда k < 0; пусть, например, k = - 1. Построим график функции 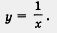 (здесь k = - 1). (здесь k = - 1).
В предыдущем параграфе мы отметили, что график функции у = -f(x) симметричен графику функции у = f(x) относительно оси х. В частности, это значит, что график функции y = - f(x) симметричен графику функции у = f(x) относительно оси x. В частности, это значит, что график функции 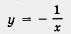 , симетричен графику , симетричен графику 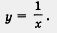 односительно оси абсцисс ( рис. 34) Таким образом, мы получим гиперболу, ветви которой расположены во втором и четвертом координатных углах. односительно оси абсцисс ( рис. 34) Таким образом, мы получим гиперболу, ветви которой расположены во втором и четвертом координатных углах.
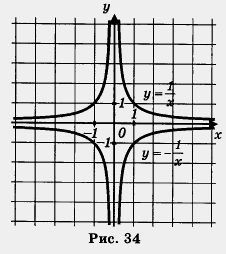
Вообще, графиком функции 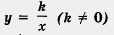 является гипербола, ветви которой расположены в первом и третьем координатных углах, если k > 0 (рис. 33), и во втором и четвертом координатных углах, если k < О (рис. 34). Точка (0; 0) — центр симметрии гиперболы, оси координат — асимптоты гиперболы. является гипербола, ветви которой расположены в первом и третьем координатных углах, если k > 0 (рис. 33), и во втором и четвертом координатных углах, если k < О (рис. 34). Точка (0; 0) — центр симметрии гиперболы, оси координат — асимптоты гиперболы.
Обычно говорят, что две величины х и у обратно пропорциональны, если они связаны соотношением ху = k (где k — число, отличное от 0), или, что то же самое, 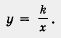 . По этой причине функцию . По этой причине функцию 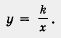 называют иногда обратной пропорциональностью (по аналогии с функцией у - kx, которую, как вы, наверное, называют иногда обратной пропорциональностью (по аналогии с функцией у - kx, которую, как вы, наверное,
помните, называют прямой пропорциональностью); число k — коэффициент обратной пропорциональности.
Свойства функции 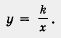 при k > 0 при k > 0
Описывая свойства этой функции, мы будем опираться на ее геометрическую модель— гиперболу (см., рис. 33).
1. Область определения функции состоит из всех чисел, кроме х = 0.
2. у > 0 при х>0;у<0 при х<0.
3. Функция убывает на промежутках (-°°, 0) и (0, +°°).
4. Функция не ограничена ни снизу, ни сверху.
5. Ни наименьшего, ни наибольшего значений у функции
6. Функция непрерывна на промежутках (-оо, 0) и (0, +оо) и претерпевает разрыв при х = 0.
Свойства функции 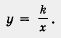 при k < 0 при k < 0
Описывая свойства этой функции, мы будем опираться на ее геометрическую модель — гиперболу (см. рис. 34).
1. Область определения функции состоит из всех чисел, кроме х = 0.
2. у > 0 при х < 0; у < 0 при х > 0.
3. Функция возрастает на промежутках (-оо, 0) и (0, +оо).
4. Функция не ограничена ни снизу, ни сверху.
5. Ни наименьшего, ни наибольшего значений у функции нет.
6. Функция непрерывна на промежутках (-оо, 0) и (0, +оо) и претерпевает разрыв при х = 0.
Пример 2. Решить уравнение 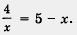
Решение.
1) Рассмотрим две функции: 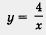 и у = 5 - х. и у = 5 - х.
2) Построим график функции 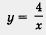 гиперболу (рис. 35). гиперболу (рис. 35).
3) Построим график линейной функции Это — прямая, ее можно построить по двум точкам (0; 5) и (5; 0). Она изображена на том же чертеже (рис. 35).
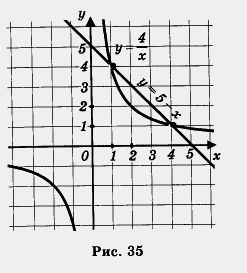
4) По чертежу устанавливаем, что гипербола и прямая пересекаются в точках А (1; 4) и В (4; 1). Проверка показывает, что это на самом деле так.
Значит, данное уравнение имеет два корня: 1 и 4 — это абсциссы точек А и Б.
Ответ: 1,4.
Пример 3. Построить и прочитать график функции у = f(x), где
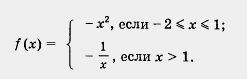
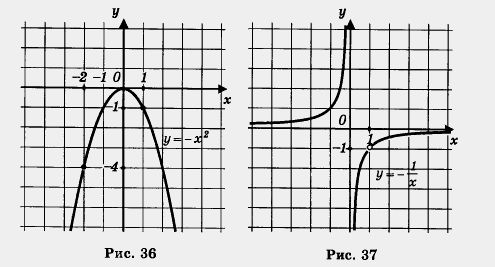
Решение. Построение графика, как обычно в таких случаях, осуществим «по кусочкам». Сначала построим параболу у = - х2 и выделим ее часть на отрезке [- 2, 1] (рис. 36).
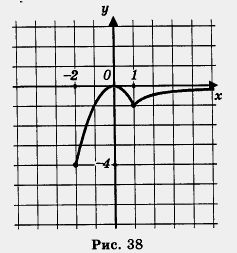
Затем построим гиперболу у и выделим ее часть на открытом луче (1, +оо) (рис. 37). Наконец, оба «кусочка» изобразим в одной системе координат — получим график функции у = f(x) (рис. 38).
Перечислим свойства функции у = f(x), т.е. прочитаем график.
1. Область определения функции — луч [-2, +оо).
2. у = 0 при х = 0; у < 0 при - 2 < д; < 0 и при я > 0.
3. Функция возрастает на промежутке [-2, 0] и [1, +оо), убывает на отрезке [0, 1].
4. Функция ограничена и снизу и сверху.
5. унаим = - 4 (достигается при х = - 2); yнаиб = 0 (достигается при х = 0).
6. Функция непрерывна в заданной области определения.
(И В заключение рассмотрим пример, считающийся достаточно сложным.
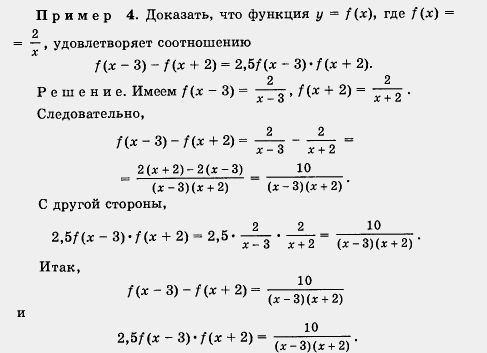
Значит, f(x - 3) - f(x + 2) = 2,5f (х - 3) . f(х + 2), что и требовалось доказать.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Видео по математикескачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|