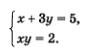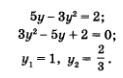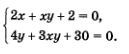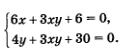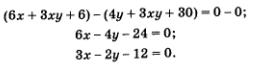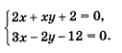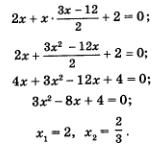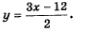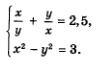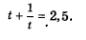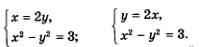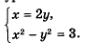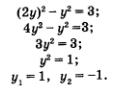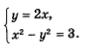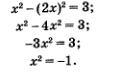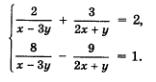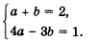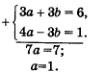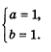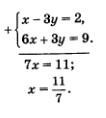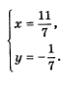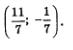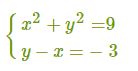|
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Методы решения систем уравнений
Какие существуют методы решения систем уравнения?В этом параграфе мы обсудим три метода решения систем уравнений, более надежные, чем графический метод, который рассмотрели в предыдущем параграфе. Метод подстановкиЭтот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений (не обязательно линейных) с двумя переменными х и у (разумеется, переменные могут быть обозначены и другими буквами, что не имеет значения). Фактически этим алгоритмом мы воспользовались в предыдущем параграфе, когда задача о двузначном числе привела к математической модели, представляющей собой систему уравнений. Эту систему уравнений мы решили выше методом подстановки (см. пример 1 из § 4). Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у. 1. Выразить у через х из одного уравнения системы. Переменные х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой. Пример 1. Решить систему уравнений Решение. 1) Выразим х через у из первого уравнения системы: х = 5 - 3у.
Метод алгебраического сложенияЭтот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода напомним на следующем примере. Пример 2. Решить систему уравнений Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения:
Если х = 2, то
Метод введения новых переменныхС методом введения новой переменной при решении рациональных уравнений с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах. Пример 3. Решить систему уравнений Решение. Введем новую переменную
х = 2 у; у — 2х. Что же дальше? А дальше каждое из двух полученных простых уравнений нужно поочередно рассмотреть в системе с уравнением х2 - у2 = 3, о котором мы пока не вспоминали. Иными словами, задача сводится к решению двух систем уравнений: Надо найти решения первой системы, второй системы и все полученные пары значений включить в ответ. Решим первую систему уравнений:
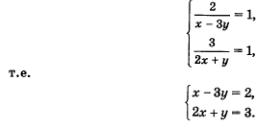
Ответ: (2; 1); (-2;-1). Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах. Первый вариант: вводится одна новая переменная и используется только в одном уравнении системы. Именно так обстояло дело в примере 3.Второй вариант: вводятся две новые переменные и используются одновременно в обоих уравнениях системы. Так будет обстоять дело в примере 4. Пример 4. Решить систему уравнений Решение. Введем две новые переменные: Учтем, что тогда Это позволит переписать заданную систему в значительно более простом виде, но относительно новых переменных а и b:
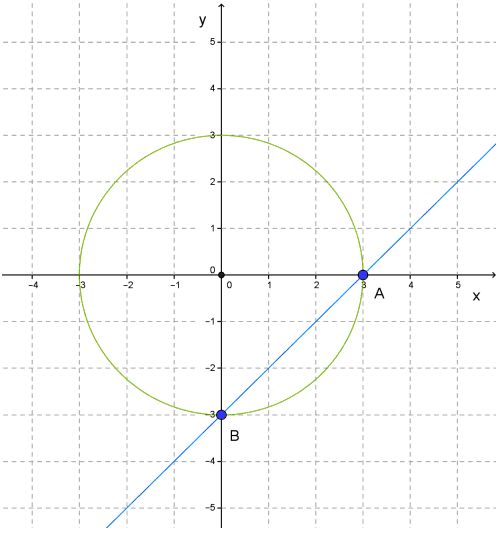
Определение. Две системы уравнений с переменными х и у называют равносильными, если они имеют одни и те же решения или если обе системы не имеют решений. Все три метода (подстановки, алгебраического сложения и введения новых переменных), которые мы обсудили в этом параграфе, абсолютно корректны с точки зрения равносильности. Иными словами, используя эти методы, мы заменяем одну систему уравнений другой, более простой, но равносильной первоначальной системе. Графический метод решения систем уравненийМы уже с вами научились решать системы уравнений такими распространенными и надежными способами, как метод подстановки, алгебраического сложения и введения новых переменных. А теперь давайте с вами вспомним, метод, который вы уже изучали на предыдущем уроке. То есть давайте повторим, что вы знаете о графическом методе решения. Метод решения систем уравнения графическим способом представляет собой построение графика для каждого из конкретных уравнений, которые входят в данную систему и находятся в одной координатной плоскости, а также где требуется найти пересечения точек этих графиков. Для решения данной системы уравнений являются координаты этой точки (x; y). Следует вспомнить, что для графической системы уравнений свойственно иметь либо одно единственное верное решение, либо бесконечное множество решений, либо же не иметь решений вообще. А теперь на каждом из этих решений остановимся подробнее. И так, система уравнений может иметь единственное решение в случае, если прямые, которые являются графиками уравнений системы, пересекаются. Если же эти прямые параллельны, то такая система уравнений абсолютно не имеет решений. В случае же совпадения прямых графиков уравнений системы, то тогда такая система позволяет найти множество решений. Ну а теперь давайте с вами рассмотрим алгоритм решения системы двух уравнений с 2-мя неизвестными графическим методом: • Во-первых, вначале мы с вами строим график 1-го уравнения; Давайте этот метод рассмотрим более подробно на примере. Нам дана система уравнений, которую необходимо решить: Решение уравнений 1. Вначале мы с вами будем строить график данного уравнения: x2+y2=9. Но следует заметить, что данным графиком уравнений будет окружность, имеющая центр в начале координат, а ее радиус будет равен трем. 2. Следующим нашим шагом будет построение графика такого уравнения, как:
y = x – 3. В этом случае, мы должны построить прямую и найти точки (0;−3) и (3;0). 3. Смотрим, что у нас получилось. Мы видим, что прямая пересекает окружность в двух ее точках A и B. Теперь мы с вами ищем координаты этих точек. Мы видим, что координаты (3;0) соответствуют точке А, а координаты (0;−3) соответственно точке В. И что мы получаем в итоге? Получившиеся при пересечении прямой с окружностью числа (3;0) и (0;−3), как раз и являются решениями обоих уравнений системы. А из этого следует, что данные числа являются и решениями этой системы уравнений. То есть, ответом этого решения являются числа: (3;0) и (0;−3). А.Г. Мордкович Алгебра 9 класс |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: