Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Приближенные значения чисел. Округление чисел

Приближенные значения чисел. Округление чисел

Из рисунка 148 видно, что масса тыквы больше чем 3 кг, но меньше чем 4 кг. Если обозначить массу тыквы (в килограммах) буквой х, то 3 < х < 4.

Число 3 называют приближенным значением х с недостатком, а число 4 — приближенным значением х с избытком.
Из рисунка 149 видно, что длина отрезка АВ заключена между 6 см и 7 см.

 Значит, 6 — приближенное значение длины отрезка АВ (в сантиметрах) > с недостатком, а 7 — с избытком.
Обозначив длину отрезка буквой у, получим: 6 < у < 1.

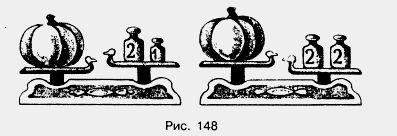
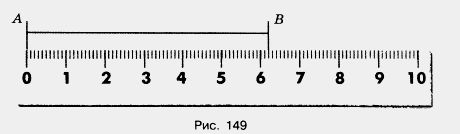
Если a < х < b, то а называют приближенным значением числа х с недостатком, a b — приближенным значением х с избытком.

Длина отрезка АВ (см. рис. 149) ближе к 6 см, чем к 7 см. Она приближенно равна 6 см.

Говорят, что число 6 получилось при округлении длины отрезка до целых.

Если масса тыквы на рисунке 148 равна 3,7 кг, то она ближе к 4 кг, чем к 3 кг (4 - 3,7 = 0,3, а 3,7 - 3 = 0,7, но 0,3 < 0,7).

Значит, масса тыквы приближенно равна 4 кг. Это число также получилось при округлении массы тыквы до целых.
Любое число, у которого 3 целых (кроме числа 3,5), а цифра десятых равна 6, 7, 8 и 9, ближе к 4, чем к 3. Поэтому при округлении этого числа до целых получаем ответ 4.

Например, 3,76 4; 3,621 4; 3,903 - 4 (знак читают: «приближенно равно»).

Если же в числе, у которого 3 целых, в разряде десятых стоит цифра 0, 1, 2, 3 или 4, то это число ближе к 3, чем к 4. Поэтому при округлении его до целых получаем ответ 3.

Например, 3,142 3;                 3,498 3;                  3,074 3.

Число 3,5 одинаково удалено и от 3, и от 4 (3,5 - 3 = 0,5 и 4 - 3,5 = 0,5).

Условились округлять его до большего числа, то есть до 4, поэтому 3,5 4.

Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых.

Числа округляют и до других разрядов — десятых, сотых, десятков, сотен и т. д.

Если число округляют до какого-нибудь разряда, то все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают.

Если первая отброшенная или замененная нулем цифра равна 5, 6, 7, 8 или 9, то стоящую перед ней цифру увеличивают на 1.

Если первая отброшенная или замененная нулем цифра равна О, 1,2,3 или 4, то стоящую перед ней цифру оставляют без изменения.

Пример 1. Округлим число 86,2759 до десятых.

Решение. Отбрасываем цифры 7, 5 и 9, которые следуют за разрядом десятых. Первая из этих цифр 7, поэтому стоящую перед ней цифру 2 увеличиваем на 1. Получаем 86,3. Пишут: 86,2759 86,3.

Пример 2. Округлим до сотен тысяч число 6 723 401.

Решение. Заменяем нулями цифры 2, 3, 4 и 1, следующие за разрядом сотен тысяч. Так как первая из них 2, то стоящую перед ней цифру 7 оставляем без изменения. Получаем число 6 700 000.

Пишут: 6 723 401 6 700 000 = 6,7 млн.

Какое число называют приближенным значением с недостатком?
Приближенным значением с избытком?
Что значит округлить число до целых?
Сформулируйте правило округления чисел
Что надо сделать с последней оставленной цифрой, если после нее идет цифра 8? цифра 5? цифра 3?

1270. Между какими соседними натуральными числами расположена каждая из дробей: 6,78; 83,74; 126,2? К какому из этих чисел дробь ближе?

1271. Длина прямоугольника х см, а его ширина у см. Укажите приближенные значения с недостатком и с избытком для периметра и для площади этого прямоугольника, если:

а) 7 < х < 8, 3 < у < 4;

б) 20 < х < 25, 16 < у < 18.

1272. Округлите до единиц дроби:

7,265;       11,638;       0,23;           8,5;        300,499;         6,5108;            0,8.

1273. Старинная русская мера массы пуд равна 16,38 кг. Округлите это значение до целых, до десятых. Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков, до сотен. Старинная русская мера длины сажень равна 2,13 м. Округлите это значение до целых, до десятых.

1274. Округлите дроби:

а) 2,781; 3,1423; 203,962; 80,46                         до десятых;
б) 0,07268; 1,35506; 10,081; 76,544; 4,455          до сотых;
в) 167,1; 2085,04; 444,4; 300,7; 137                    до десятков.

1275. Одна деталь имеет массу 13,26 кг, вторая — 14,43 кг, третья — 1,66 кг, а четвертая — 15,875 кг. Найдите общую массу этих четырех деталей и округлите результат до десятых долей килограмма. Сравните ответ с результатом, полученным, если сначала округлить данные задачи до десятых долей, а потом ее решить.

1276. Трасса лыжных гонок состоит из 4 участков. Первый участок имеет длину 4,35 км, второй — 5,75 км, третий — 6,95 км и четвертый — 2,8 км. Найдите длину всей трассы и округлите ответ:

а) до десятых долей километра;

б) до целых километров.

1277. Найдите периметр четырехугольника ABCD, если АВ = 6,2 дм, CD больше АВ на 3,14 дм, но меньше ВС на 2,31 дм; AD больше ВС на 1,2 дм. Ответ округлите:

а) до десятых долей дециметра;

б) до целых дециметров.

1278. Вычислите устно:

1279. Восстановите цепочку вычислений:

1280. На координатном луче число х расположено между числами а и b.

Определите, к какому из чисел ближе х, если:

а) а = 2,3, b = 2,7, x = 2,6;                в) а = 5,6, b = 5,7, x = 5,65.
б) а = 1,34, b= 1,35, х = 1,342;

1281. К числу 76 890 приписали справа нуль, два нуля, три нуля. Во сколько раз увеличилось число? Прочитайте каждое из получившихся чисел.

1282. В числе 89 452 200 зачеркнули два последних нуля. Во сколько раз уменьшилось число?

1283. Укажите два числа, которые на координатном луче расположены между числами:

а) 2,1 и 2,2;         в)0 и 0,02;
b)0,8 и 0,9;          г) 3,1 и 3,11.

1284. Шахматная доска состоит из 8 рядов, по 8 клеток в каждом из них. Какую часть доски составляет:

а) один ряд клеток;           в) одна клетка;
б) 3 ряда клеток;               г) 7 клеток?

Шахматный конь может двигаться на две клетки по вертикали или горизонтали и на одну клетку в сторону.
Подумайте, может ли конь переместиться из клетки А шахматной доски в клетку В.

1285. Какую часть кубического метра составляет:

а) 1 л;          б) 10 дм³;         в) 100 л;         г) 100 см³?

1286. Найдите число, которое:

1287. Используя рисунок 150, найдите число а:

1288. Согласны ли вы с утверждением: «Если участки огорожены заборами одинаковой длины, то площади этих участков равны»? Подтвердите свое мнение примерами.

1289. Скорость течения реки 60 м/мин. Продвигается ли лодка, в каком направлении и с какой скоростью, если ее собственная скорость:

а) 90 м/мин направлена по течению;
б) 90 м/мин направлена против течения;
в) 60 м/мин направлена по течению;
г) 60 м/мин направлена против течения?

1290. Запишите 4 числа, первое из которых 4,612, а каждое следующее на 2,154 больше предыдущего.

1291. Найдите значение выражения 84 - а и выражения а + 6,546 , если а = 30,4; 2,454; 83,998.

1292. Представьте произведение 2,75 ■ 3 в виде суммы и найдите его значение.

1293. Выполните действия:

а) 68,7 - (44 + 0,375);                     в) 504 - 47,9 + (58,7 - 49);
б) 90,4 + 65,4 - 90,8;                      г) 17,654 - (37 - 22,9) + 0,345.

1294. Вместо звездочки поставьте знак >, = или < так, чтобы получилось верное равенство или неравенство:

а) 0,483 * 0,479;              в) 95,3 * 95,300;
б) 4,781 * 4,79;                г) 0,045 * 0,0045.

1295. Собственная скорость лодки 4,5 км/ч, скорость течения 2,5 км/ч. Найдите скорость лодки при движении по течению и против течения. Какой путь пройдет лодка по течению за 4 ч и какой путь она пройдет против течения за 3 ч?

1296. Решите задачу:

1) В школу завезли 24 т угля. За зиму израсходовали привезенного угля. Сколько тонн угля осталось?
2) Маляры израсходовали - купленной краски для ремонта школы. Сколько краски осталось, если купили ее 300 кг?

1297. Округлите дроби:

а) 1,69; 1,198; 37,444; 37,5444; 802,3022 до целых;
б) 0,3691; 0,8218; 0,9702; 81,3501 до десятых.

1298. Для каждого из чисел найдите натуральные приближенные значения с недостатком и с избытком: 3,97; 21,609; 10,394; 1,057.

1299. Запишите число, которое:

а) меньше миллиона в 10 раз; на 10;
б) больше миллиона в 10 раз; на 10;
в) больше числа 709 в 100 раз; в 1000 раз;
г) меньше числа 623 100 000 в 10 раз; в 1000 раз; в 100 000 раз.

1300. Найдите значение выражения:

а) 8000 • 60 000; в) 250 000 • 600 • 40;
б) 1700 • 800 000; г) 19 000 • 20 000 • 50.

1301. Собственная скорость теплохода 21,6 км/ч. Скорость течения 4,9 км/ч. Найдите скорость теплохода по течению и против течения.

1302. Теплоход шел по озеру 3 ч со скоростью 27 км/ч, а потом 4 ч по реке, впадающей в это озеро. Найдите весь путь, который прошел теплоход за эти 7 ч, если скорость течения реки 3 км/ч.

1303. В сокровищнице Кощея Бессмертного 32 000 ларцов, в каждом ларце 210 одинаковых по массе слитков золота и серебра. Какова масса запасов золота и серебра у Кощея, если масса десятка слитков 900 г?

1304. Поставьте вместо звездочек пропущенные цифры:

В науке ы промышленности, в сельском хозяйстве при расчетах десятичные дроби используются значительно чаще, чем обыкновенные.

Это связано с простотой правил вычислений с десятичными дробями, похожестью их на правила действий с натуральными числами.

Правила вычислении с десятичными дробями описал знаменитый ученый Средневековья аль-Кашп Джемшйд Ибн Масуд, работавший в городе Самарканде в обсерватории Улугбека в начале XV века.

Записывал аль-Каши десятичные дроби так же, как принято сейчас, но он не пользовался запятой: дробную часть он записывал красными чернилами или отделял вертикальной чертой.

Но об этом в Европе в то время не узнали, и только через 150 лет десятичные дроби были заново изобретены фламандским инженером и ученым Симоном Стевином. Стевин записывал десятичные дроби довольно сложно.

Например, число 24,56 выглядело так: — вместо запятой нуль в кружке (или 0 над целой частью), цифрами 1, 2, 3, ... помечалось положение остальных знаков.

Запятая или точка для отделения целой части стали использоваться с XVII века.

В России учение о десятичных дробях изложил Леонтий Филиппович Магницкий в 1703 году в первом учебнике математики «Арифметика, сирень наука числительная».

Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений

_{Школьная библиотека онлайн, учебники и книги по всему предметам, Математика 5 класс скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.