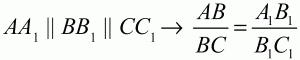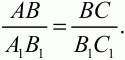|
Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Теорема Фалеса. Полные уроки
Тема урока
Цели урока
Задачи урока
План урока
Историческая справкаФалес.
Несмотря на огромное значение, которое он имеет, о нем мало известно. Будучи купцом, он использовал торговые поездки в целях расширения научных сведений и знания, которые он приобрел в Финикии и Египте – перенес в Грецию Он был гидроинженером, прославившимся своими работами, разносторонним учёным и мыслителем, изобретателем астрономических приборов. Как учёный он широко прославился в Греции, сделав удачное предсказание солнечного затмения, наблюдавшегося в Греции в 585 г. до н.э. Для этого предсказания Фалес использовал почерпнутые им в Египте астрономические сведения, восходящие к наблюдениям и обобщениям вавилонской науки. По свидетельствам Геродота и Диогена Фалес приобрел славу своей мудростью, причем весьма практической. Например, основываясь на своих знаниях однажды он предсказал обильный урожай оливок, и, арендовав маслобойню, получил большую прибыль. Фалес также входил в число знаменитых семи мудрецов, чьи изречения дошли до наших дней. Ему приписывают следующие:
Земля, с точки зрения философа, держится на воде и окружена со всех сторон океаном. Она пребывает на воде, как диск или доска, плавающая на поверхности водоёма. Фалесу принадлежит попытка разобраться и в строении окружающей Землю вселенной, определить, в каком порядке расположены по отношению к Земле небесные светила: Луна, Солнце, звёзды. И в этом вопросе Фалес опирался на результаты вавилонской науки. Но ему представлялся порядок светил обратный тому, что существует в действительности: он полагал, что ближе всего к Земле находится так называемое небо неподвижных звёзд, а дальше всего – Солнце. Эта ошибка была исправлена его продолжателями. Хотя идея Фалеса о первосущности представляется нам сейчас наивной, но с исторической точки зрения она чрезвычайно важна: в положении “все из воды” была дана отставка языческим богам, в конечном счете мифологическому мышлению, и продолжен путь к естественному объяснению природы. Фалесу впервые пришла мысль о единстве мироздания. Эта идея, однажды родившись, никогда уже не умирала: она сообщалась его ученикам и ученикам его учеников. Разносторонние познания Фалеса имели определенное влияние на развитие его философского мышления. Так, например, геометрия в то время была настолько развитой наукой, что являлась определенной основой научной абстракции. Именно это и повлияло на взгляды Фалеса.
Фалес как геометр и его трудыФалес известен и как геометр. Условно ему приписывают открытие и доказательство ряда теорем: о делении круга диаметром пополам, о равенстве углов при основании равнобедренного треугольника, о равенстве вертикальных углов, один из признаков равенства прямоугольных треугольников и другие. Фалес открыл любопытный способ определения расстояния от берега до видимого корабля. Одни историки утверждают, что для этого им был использован признак подобия прямоугольных треугольников. Потомки Фалеса обязаны ему тем, что он, пожалуй, впервые ввел в науку, и в частности в математику, доказательство. Известно сейчас, что многие математические правила были открыты намного раньше, чем в Греции. Но все - опытным путем. Строго логическое доказательство правильности каких-либо предложений на основании общих положений, принятых за достоверные истины, было изобретено греками. Характерно и совершенно новая черта греческой математики заключается в постепенном переходе при помощи доказательства от одного предположения к другому. Именно такой характер математике был предан Фалесом. И даже сегодня, через 25 веков, приступая к доказательству, например, теоремы о свойствах ромба, вы, в сущности, рассуждаете почти так, как это делали ученики Фалеса. Трудно сейчас сказать, что в научном перечне принадлежит действительно Фалесу и что приписано ему потомками, восхищенными его гением. Несомненно, в лице Фалеса Греция впервые обрела одновременно философа, математика и естествоиспытателя. Не случайно древние причислили его к "великолепной семерке" мудрецов древности.
Полезно вспомнитьДве прямые AB и CD (рис.) называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать. Обозначение: AB|| CD. Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой. Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Угол между двумя параллельными лучами равен нулю, если у них одинаковые направления, и 180°, если их направления противоположны.
При пересечении двух параллельных прямых третьей прямой, образуются восемь углов (рис.), которые попарно называются: 1) соответственные углы ( 1 и 5; 2 и 6; 3 и 7; 4 и 8 ); эти углы попарно
Теорема Фалеса
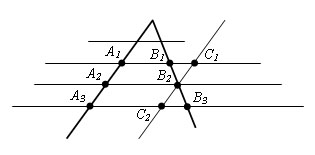
Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. Справедливо и более общее утверждение, называемое обобщенной теоремой Фалеса: отрезки, высекаемые параллельными прямыми на одной прямой, пропорциональны отрезкам на другой прямой. Никакие труды Фалеса до нас не дошли и их содержание историки науки восстанавливают по косвенным данным. Фалесу приписывают доказательства семи геометрических теорем, среди них приведенную выше, а также теорему о равенстве вертикальных углов. В иностранных учебниках геометрии теоремой Фалеса называется утверждение о том, что вписанный угол, опирающийся на диаметр, прямой. Теорема. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Пусть точки A1, A2, A3 – точки пересечения параллельных прямых с одной из сторон угла. А точки B1, B2, B3 – соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A1A2 = A2A3, то B1B2=B2B3.
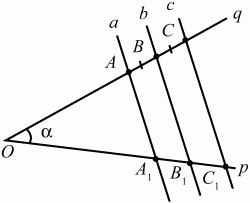
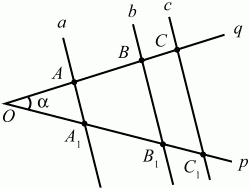
Теорема о пропорциональных отрезках (обобщение теоремы Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки. или
Интересный факт
Морская навигация
Открытия и заслуги ее автораА известно ли вам, что Фалес Милетский был одним из семи самых известных по тем временам, мудрецом Греции. Он основал Ионийскую школу. Идею, которую продвигал Фалес в этой школе, было единство всего сущего. Мудрец считал, что есть единое начало, от которого произошли все вещи. Огромной заслугой Фалеса Милетского является создание научной геометрии. Этот великий учений сумел с египетского искусства измерения создать дедуктивную геометрию, базой которой есть общие основания. Кроме огромных познаний в геометрии, Фалес еще и неплохо разбирался в астрономии. Эму первому удалось предсказать полное затмение Солнца. А ведь это происходило не в современном мире, а в далеком 585 году, еще до нашей эры. Фалес Милетский был тем человеком, который сообразил, что север можно точно определить по созвездию Малой Медведицы. Но и это не было его последним открытием, так как он сумел в точности определить продолжительность года, разбить его на триста шестьдесят пять дней, а также установил время равноденствий. Фалес на самом деле был всесторонне развитым и мудрым человеком. Кроме того, что он славился как прекрасный математик, физик, астроном, он еще и как настоящий метеоролог, смог довольно точно предсказать урожай оливок. Но самое примечательное то, что Фалес никогда не ограничивался в своих познаниях только научно-теоретической областью, а всегда пытался закрепить доказательства своих теорий на практике. И самое интересное, то, что великий мудрец не сосредотачивался на какой-то одной области своих познаний, его интерес имел различные направленности. Имя Фалеса стало нарицательным для мудреца уже тогда. Его важность и значимость для Греции была так велика, как для России имя Ломоносова. Конечно, его мудрость можно толковать по-разному. Но точно можно сказать, что ему были присущи и изобретательность, и практическая смекалка, и в какой-то степени отрешенность. Фалес Милетский был отличным математиком, философом, астрономом, любил путешествовать, был купцом и предпринимателем, занимался торговлей, а также был неплохим инженером, дипломатом, провидцем и активно участвовал в политической жизни. Он даже умудрился с помощью посоха и тени определить высоту пирамиды. А было это так. В один погожий солнечный день Фалес поставил свой посох на границе, где заканчивалась тень от пирамиды. Далее он дождался, когда длинна от тени его посоха сравнялась с его высотой, и замерил длину тени пирамиды. Вот так, казалось бы просто Фалес определил высоту пирамиды и доказал, что длина одной тени имеет отношение к длине другой тени, также, как и высота пирамиды относится к высоте посоха. Чем и поразил самого фараона Амасиса. Благодаря Фалесу все известные в то время знания были переведены в область научного интереса. Он смог донести результаты до уровня, пригодного для научного потребления, выделив определенный комплекс понятий. И возможно с помощью Фалеса началось последующее развитие античной философии. Теорема Фалеса играет одну важных ролей в математике. Она была известна не только в Древнем Египте и Вавилоне, но и в других странах и являлась почвой для развития математики. Да и в повседневной жизни, при строительстве зданий, сооружений, дорог и т.д., без теоремы Фалеса не обойтись. Теорема Фалеса в культуреТеорема Фалеса прославилась не только в математике, но ее приобщили еще и к культуре. Однажды аргентинская музыкальная группа Les Luthiers (исп.) на суд зрителей представила песню, которую посвятила известной теореме. Участники Les Luthiers в своем видеоклипе специально для этой песни предоставили доказательства для прямой теоремы для пропорциональных отрезков. Вопросы
Список использованных источников
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: