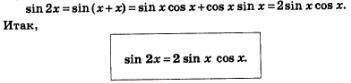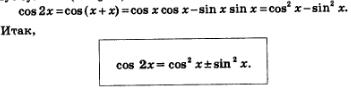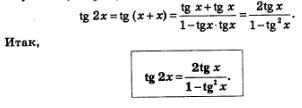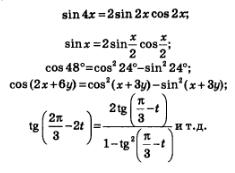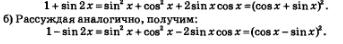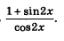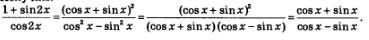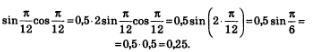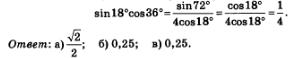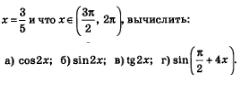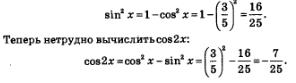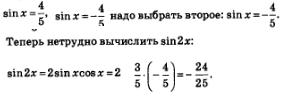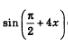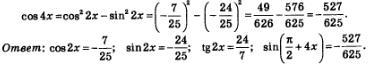|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Формулы двойного аргумента
§ 24. Формулы двойного аргумента
Здесь речь пойдет о формулах тригонометрии, позволяющих выразить 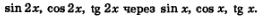 Эти формулы обычно называют формулами двойного аргумента. Название, может быть, не очень удачно, как, впрочем, и такие названия, как "формулы приведения», «синус суммы», «косинус разности» и т.д., но это не суть важно: главное, что есть некий словесный символ, позволяющий посвященным понять, о чем идет речь. Эти формулы обычно называют формулами двойного аргумента. Название, может быть, не очень удачно, как, впрочем, и такие названия, как "формулы приведения», «синус суммы», «косинус разности» и т.д., но это не суть важно: главное, что есть некий словесный символ, позволяющий посвященным понять, о чем идет речь.
Рассмотрим выражение sin2х, представив при этом 2х в виде х+х. Это позволит применить к выражению sin (х+ х)формулу «синус суммы» (см. § 21). Имеем:
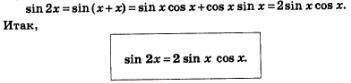
Рассмотрим выражение соs2х, представив при этом 2х в виде х+х. Это позволит применить к выражению соs (х+х) формулу «косинус суммы» (см. § 21). Имеем:
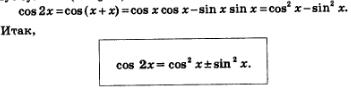
Рассмотрим выражение tg 2х, представив при этом 2х в виде х+х. Это позволит применить к выражению tg (х+х) формулу «тангенс суммы» (см. § 23). Имеем:
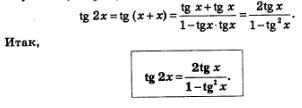
Формулы «синус двойного аргумента» и «косинус двойного аргумента» справедливы для любых значений аргумента (никаких ограничений нет), тогда как формула «тангенс двойного аргумента» справедлива лишь для тех значений аргумента х, для которых определены tg х и tg 2 х, а также отличен от нуля знаменатель дроби, т.е. 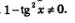
Разумеется, формулы двойного аргумента можно применять и в тех случаях, когда место аргумента х занимает более сложное выражение. Так, справедливы следующие соотношения:
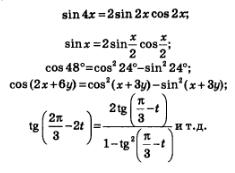
И, как всегда, любую из трех полученных в этом параграфе формул двойного аргумента можно использовать в написании как справа налево, так и слева направо. Например,
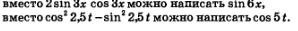
Пример 1. Доказать тождества:
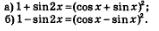
Решение: а) Воспользуемся тем, что 1 = sin2 х + соз2 х, и формулой синуса двойного аргумента. Получим:
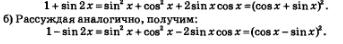
Пример 2. Сократить дробь 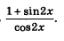
Решение. В числителе дроби воспользуемся доказанным в примере 1 а тождеством, а в знаменателе — формулой косинуса двойного аргумента. Получим:
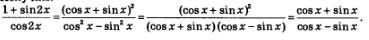
Пример3.Вычислить: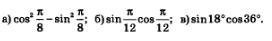
Решение: а) Заданное выражение представляет собой правую часть формулы косинуса двойного аргумента. Заметив это, получим
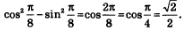
б) Заданное выражение представляет собой правую часть формулы синуса двойного аргумента, но только не хватает множителя 2. Введя его, получим:
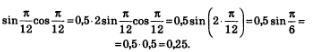
в) Этот пример значительно сложнее, но зато он красивее предыдущих: здесь нужно догадаться умножить и разделить заданное выражение на 4соs18°. Что это даст? Смотрите:
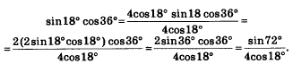
Как видите, мы дважды воспользовались формулой синуса двойного аргумента. Чтобы довести вычисления до конца, заметим, что 72°=90°-18°. Значит, sin 720=sin (90°-180)=соs180. Таким образом,
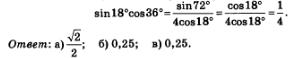
Пример 4. Доказать тождество 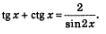
Решение. Преобразуем левую часть доказываемого тождества:
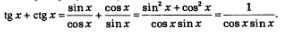
Умножив и числитель, и знаменатель последней дроби на 2 («подгоняем» знаменатель под формулу синуса двойного аргумента), получим:
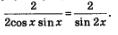
Итак, 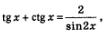 что и требовалось доказать. что и требовалось доказать.
Замечание. Еще раз обращаем ваше внимание на то, что тождество доказано лишь для допустимых значении х, конкретнее для 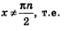
для значений х, при которых имеющиеся знаменатели отличны от нуля.
Пример 5. Зная, что
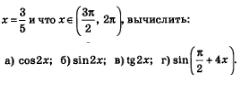
Решение: а) Воспользуемся формулой sin2 х + соз2 х = 1. Имеем:
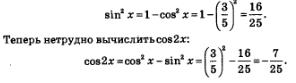
б) Для вычисления sin2х воспользуемся формулой sin 2х = 2 sin хсоз x.
Значение соз х дано в условии, а значение sin х найдем следующим образом. Во-первых, мы уже знаем, что 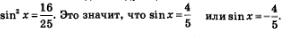
Во-вторых, по условию аргумент х принадлежит четвертой четверти, а в ней синус отрицателен. Это значит, что из двух значении
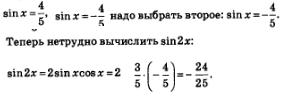
в) tg2х вычислим, воспользовавшись определением тангенса:

г) Для вычисления 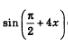 сначала воспользуемся формулой приведения: сначала воспользуемся формулой приведения: 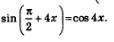
Применим к выражению соз4x формулу косинуса двойного аргумента: соз4х=соз2 2х - sin2 2х. Воспользуемся тем, что значения соз 2х и sin 2xуже найдены нами:
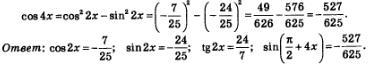
Пример 6. Решить уравнение sin4х-соз2х=0.
Решение. Если в левой части уравнения применить к выражению sin4x формулу синуса двойного аргумента, то удастся разложить левую часть на множители. Имеем последовательно:
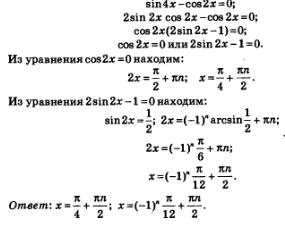
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|