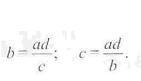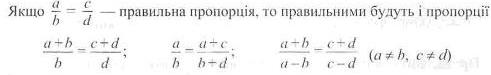|
|
|
| Строка 5: |
Строка 5: |
| | [[Image:Asd180.jpg|550px|Математика]]<br> | | [[Image:Asd180.jpg|550px|Математика]]<br> |
| | | | |
| - | У правильній пропорції добуток крайніх членів дорівнює добутку середніх членів.<br><br>Цю властивість називають '''основною властивістю [[Композиція_в_графіці_–_пропорції,_масштаб._Художні_прийоми_виявлення_характеру_і_образності_природних_форм._Презентація_уроку|пропорції]].'''<br><br> | + | У правильній пропорції добуток крайніх членів дорівнює добутку середніх членів.<br><br>Цю властивість називають '''основною властивістю [[Композиція в графіці – пропорції, масштаб. Художні прийоми виявлення характеру і образності природних форм. Презентація уроку|пропорції]].'''<br><br> |
| | | | |
| | [[Image:Asd181.jpg|550px|пропорції]]<br> | | [[Image:Asd181.jpg|550px|пропорції]]<br> |
| Строка 11: |
Строка 11: |
| | Щоб знайти крайній член пропорції, потрібно добуток її середніх членів поділити на інший крайній член.<br><br>'''Аналогічно'''<br>[[Image:Asd182.jpg]]<br> | | Щоб знайти крайній член пропорції, потрібно добуток її середніх членів поділити на інший крайній член.<br><br>'''Аналогічно'''<br>[[Image:Asd182.jpg]]<br> |
| | | | |
| - | Щоб знайти середній член пропорції, потрібно добуток її крайніх членів поділити на інший середній член.<br>'''<br>Для тих, хто хоче знати більше'''<br>[[Image:Asd183.jpg|550px| Для тих, хто хоче знати більше]]<br> | + | Щоб знайти середній член пропорції, потрібно добуток її крайніх членів поділити на інший середній член.<br>'''<br>Для тих, хто хоче знати більше'''<br>[[Image:Asd183.jpg|550px|Для тих, хто хоче знати більше]]<br> |
| | | | |
| - | [[Image:Asd184.jpg|550px| Для тих, хто хоче знати більше]]<br> | + | [[Image:Asd184.jpg|550px|Для тих, хто хоче знати більше]]<br> |
| | | | |
| | [[Image:Asd185.jpg|550px|Математика]]<br> | | [[Image:Asd185.jpg|550px|Математика]]<br> |
| Строка 27: |
Строка 27: |
| | [[Image:Asd190.jpg]]<br> | | [[Image:Asd190.jpg]]<br> |
| | | | |
| - | <br>'''Здогадайтеся'''<br>681. Для перевезення зерна заготували мішки двох видів, в одні вміщується по 60 кг зерна, а в інші — по 80 кг. Скільки потрібно мішків кожного виду, щоб перевезти 1 т зерна, якщо всі мішки повинні бути заповнені повністю? | + | <br>'''Здогадайтеся'''<br>681. Для перевезення зерна заготували мішки двох видів, в одні вміщується по 60 кг зерна, а в інші — по 80 кг. Скільки потрібно мішків кожного виду, щоб перевезти 1 т зерна, якщо всі мішки повинні бути заповнені повністю? |
| | | | |
| - | <br>'''Цікаві розповіді<br>Пропорція і музика'''<br>Слово «пропорція» (від латинського ргорогііо) означає «співрозмірність», «певне відношення частин між собою».<br>За допомогою пропорцій розв'язували задачі ще в стародавні часи. Повну теорію пропорцій було створено у [[Відеоматеріал_на_тему_«Храми_Древньої_Греції»|Стародавній Греції]] в IV ст. до н. е. здебільшого в працях учених Евдокса Кнідського та Теетета. | + | <br>'''Цікаві розповіді<br>Пропорція і музика'''<br>Слово «пропорція» (від латинського ргорогііо) означає «співрозмірність», «певне відношення частин між собою».<br>За допомогою пропорцій розв'язували задачі ще в стародавні часи. Повну теорію пропорцій було створено у [[Відеоматеріал на тему «Храми Древньої Греції»|Стародавній Греції]] в IV ст. до н. е. здебільшого в працях учених Евдокса Кнідського та Теетета. |
| | | | |
| - | <br>Теорію пропорцій досконало висвітлено у «Началах» Евкліда, зокрема, там є доведення й основної властивості пропорції. | + | <br>Теорію пропорцій досконало висвітлено у «Началах» Евкліда, зокрема, там є доведення й основної властивості пропорції. |
| | | | |
| - | <br>Стародавні греки називали вчення про відношення і пропорції музикою, яку вважали галуззю математики. Вони знали, що слабше натягнута струна дає нижчий («товстіший») звук, а тугіше натягнута струна — вищий звук. Але в кожному струнному музичному інструменті є не одна, а кілька струн. Щоб усі струни під час гри звучали «узгоджено», приємно для слуху людини, їхні довжини (а за однакових довжин — товщини) повинні перебувати у певному відношенні. Тому вчення про відношення і пропорції стародавні греки називали [[Музика_6_клас|музикою]]. | + | <br>Стародавні греки називали вчення про відношення і пропорції музикою, яку вважали галуззю математики. Вони знали, що слабше натягнута струна дає нижчий («товстіший») звук, а тугіше натягнута струна — вищий звук. Але в кожному струнному музичному інструменті є не одна, а кілька струн. Щоб усі струни під час гри звучали «узгоджено», приємно для слуху людини, їхні довжини (а за однакових довжин — товщини) повинні перебувати у певному відношенні. Тому вчення про відношення і пропорції стародавні греки називали [[Музика 6 клас|музикою]]. |
| | | | |
| - | <br>Пропорційність використовувалася і використовується сьогодні в мистецтві, архітектурі. Використання пропорційності в архітектурі, живописі, скульптурі означає дотримання певних співвідношень між окремими частинами споруди, картини, скульптури тощо. | + | <br>Пропорційність використовувалася і використовується сьогодні в мистецтві, архітектурі. Використання пропорційності в архітектурі, живописі, скульптурі означає дотримання певних співвідношень між окремими частинами споруди, картини, скульптури тощо. |
| | | | |
| - | <br>Сучасний запис пропорції (а : b = с : d) увів на початку XVIII ст. німецький математик Г. Лейбніц.<br><br>'''<br>Вправи для повторення'''<br>682. Площа квадрата дорівнює 25 см<sup>2</sup>. Чому дорівнює площа квадрата, сторона якого удвічі більша від сторони даного [[Делим_квадрат_на_части|квадрат]]а? | + | <br>Сучасний запис пропорції (а : b = с : d) увів на початку XVIII ст. німецький математик Г. Лейбніц.<br><br>'''<br>Вправи для повторення'''<br>682. Площа квадрата дорівнює 25 см<sup>2</sup>. Чому дорівнює площа квадрата, сторона якого удвічі більша від сторони даного [[Делим квадрат на части|квадрата]]? |
| | | | |
| - | <br>683. Автомобіль, рухаючись зі швидкістю 70 км/год, подолав шлях між двома містами за 3 год. За який час подолає цей шлях мотоцикліст, який рухається зі швидкістю 40 км/год? | + | <br>683. Автомобіль, рухаючись зі швидкістю 70 км/год, подолав шлях між двома містами за 3 год. За який час подолає цей шлях мотоцикліст, який рухається зі швидкістю 40 км/год? |
| | | | |
| - | <br>684. Тарас робить 3 кроки за 5 с, а Сергій — 5 кроків такої ж довжини за 8 с. Хто із хлопців ходить швидше? | + | <br>684. Тарас робить 3 кроки за 5 с, а Сергій — 5 кроків такої ж довжини за 8 с. Хто із хлопців ходить швидше? |
| | | | |
| - | <br>685. Перший робітник за 8хв виготовив 3 деталі, а другий за 10хв — 4 такі ж деталі. У котрого з робітників продуктивність праці вища? | + | <br>685. Перший робітник за 8хв виготовив 3 деталі, а другий за 10хв — 4 такі ж деталі. У котрого з робітників продуктивність праці вища? |
| | | | |
| | <br>686. Маса 4 однакових деталей дорівнює 21,6 кг. Яка маса 15 таких же деталей? | | <br>686. Маса 4 однакових деталей дорівнює 21,6 кг. Яка маса 15 таких же деталей? |
| | | | |
| | + | <br> ''Математика [[6 клас уроки|6 клас]] Галина Янченко, Василь Кравчук '' |
| | | | |
| - | ''Математика [[6_клас_уроки|6 клас]] Галина Янченко, Василь Кравчук ''
| + | ''Вислано читачами iнтернет-сайту'' |
| - | | + | |
| - | ''Вислано читачами iнтернет-сайту'' | + | |
| | | | |
| | <br> <sub>[[Гіпермаркет Знань - перший в світі!|Онлайн-бібліотека з підручниками]] і книгами, тести [[Математика|з математики]], завдання [[Математика 6 клас|з математики 6 клас]], календарне планування</sub> | | <br> <sub>[[Гіпермаркет Знань - перший в світі!|Онлайн-бібліотека з підручниками]] і книгами, тести [[Математика|з математики]], завдання [[Математика 6 клас|з математики 6 клас]], календарне планування</sub> |
| | | | |
| - | '''<u>Зміст уроку | + | '''<u>Зміст уроку</u>'''<u> |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B2%D0%B8%D1%87%D0%B0%D0%B9%D0%BD%D0%B8%D1%85_%D0%B4%D1%80%D0%BE%D0%B1%D1%96%D0%B2._%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D1%83_%D1%96_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%B8%D0%B9_%D0%BA%D0%B0%D1%80%D0%BA%D0%B0%D1%81 конспект уроку і опорний каркас] | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B2%D0%B8%D1%87%D0%B0%D0%B9%D0%BD%D0%B8%D1%85_%D0%B4%D1%80%D0%BE%D0%B1%D1%96%D0%B2._%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D1%83_%D1%96_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%B8%D0%B9_%D0%BA%D0%B0%D1%80%D0%BA%D0%B0%D1%81 конспект уроку і опорний каркас] ''' |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентація уроку | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9F%D1%80%D0%BE%D0%BF%D0%BE%D1%80%D1%86%D1%96%D1%8F._%D0%9F%D1%80%D0%B5%D0%B7%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D1%96%D1%8F_%D1%83%D1%80%D0%BE%D0%BA%D1%83 презентація уроку] |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративні методи та інтерактивні технології | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративні методи та інтерактивні технології |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] закриті вправи (тільки для використання вчителями) | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] закриті вправи (тільки для використання вчителями) |
Текущая версия на 10:05, 27 декабря 2012
Гіпермаркет Знань>>Математика>>Математика 6 клас>>Пропорція


У правильній пропорції добуток крайніх членів дорівнює добутку середніх членів.
Цю властивість називають основною властивістю пропорції.

Щоб знайти крайній член пропорції, потрібно добуток її середніх членів поділити на інший крайній член.
Аналогічно
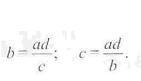
Щоб знайти середній член пропорції, потрібно добуток її крайніх членів поділити на інший середній член.
Для тих, хто хоче знати більше

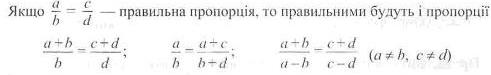






Здогадайтеся
681. Для перевезення зерна заготували мішки двох видів, в одні вміщується по 60 кг зерна, а в інші — по 80 кг. Скільки потрібно мішків кожного виду, щоб перевезти 1 т зерна, якщо всі мішки повинні бути заповнені повністю?
Цікаві розповіді
Пропорція і музика
Слово «пропорція» (від латинського ргорогііо) означає «співрозмірність», «певне відношення частин між собою».
За допомогою пропорцій розв'язували задачі ще в стародавні часи. Повну теорію пропорцій було створено у Стародавній Греції в IV ст. до н. е. здебільшого в працях учених Евдокса Кнідського та Теетета.
Теорію пропорцій досконало висвітлено у «Началах» Евкліда, зокрема, там є доведення й основної властивості пропорції.
Стародавні греки називали вчення про відношення і пропорції музикою, яку вважали галуззю математики. Вони знали, що слабше натягнута струна дає нижчий («товстіший») звук, а тугіше натягнута струна — вищий звук. Але в кожному струнному музичному інструменті є не одна, а кілька струн. Щоб усі струни під час гри звучали «узгоджено», приємно для слуху людини, їхні довжини (а за однакових довжин — товщини) повинні перебувати у певному відношенні. Тому вчення про відношення і пропорції стародавні греки називали музикою.
Пропорційність використовувалася і використовується сьогодні в мистецтві, архітектурі. Використання пропорційності в архітектурі, живописі, скульптурі означає дотримання певних співвідношень між окремими частинами споруди, картини, скульптури тощо.
Сучасний запис пропорції (а : b = с : d) увів на початку XVIII ст. німецький математик Г. Лейбніц.
Вправи для повторення
682. Площа квадрата дорівнює 25 см2. Чому дорівнює площа квадрата, сторона якого удвічі більша від сторони даного квадрата?
683. Автомобіль, рухаючись зі швидкістю 70 км/год, подолав шлях між двома містами за 3 год. За який час подолає цей шлях мотоцикліст, який рухається зі швидкістю 40 км/год?
684. Тарас робить 3 кроки за 5 с, а Сергій — 5 кроків такої ж довжини за 8 с. Хто із хлопців ходить швидше?
685. Перший робітник за 8хв виготовив 3 деталі, а другий за 10хв — 4 такі ж деталі. У котрого з робітників продуктивність праці вища?
686. Маса 4 однакових деталей дорівнює 21,6 кг. Яка маса 15 таких же деталей?
Математика 6 клас Галина Янченко, Василь Кравчук
Вислано читачами iнтернет-сайту
Онлайн-бібліотека з підручниками і книгами, тести з математики, завдання з математики 6 клас, календарне планування
Зміст уроку
 конспект уроку і опорний каркас конспект уроку і опорний каркас
 презентація уроку презентація уроку
 акселеративні методи та інтерактивні технології акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями) закриті вправи (тільки для використання вчителями)
 оцінювання
Практика оцінювання
Практика
 задачі та вправи,самоперевірка задачі та вправи,самоперевірка
 практикуми, лабораторні, кейси практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання
Ілюстрації домашнє завдання
Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати реферати
 фішки для допитливих фішки для допитливих
 шпаргалки шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення
 зовнішнє незалежне тестування (ЗНТ) зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні підручники основні і допоміжні
 тематичні свята, девізи тематичні свята, девізи
 статті статті
 національні особливості національні особливості
 словник термінів словник термінів
 інше
Тільки для вчителів інше
Тільки для вчителів
 ідеальні уроки ідеальні уроки
 календарний план на рік календарний план на рік
 методичні рекомендації методичні рекомендації
 програми програми
 обговорення обговорення
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|