|
|
| Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>>Математика:Параллельные прямые в пространстве ''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>>Математика:Параллельные прямые в пространстве ''' |
| | | | |
| - | <br> '''ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ''' | + | <br> '''Параллельные прямые в пространстве''' |
| | | | |
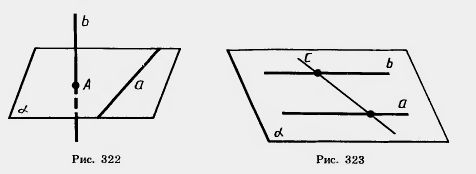
| - | <br>'''''Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися''''' (рис. 322). | + | <br>Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися (рис. 322). |
| | | | |
| | <br> | | <br> |
| | | | |
| - | [[Image:30-06-1.jpg]]<br> <br>Задача (3). Докажите, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости. | + | [[Image:30-06-1.jpg|550px| Параллельные прямые в пространстве ]]<br> <br>Задача (3). Докажите, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости. |
| | | | |
| | Решение. Так как данные прямые а и b параллельны, то через них можно провести плоскость (рис. 323). Обозначим ее [[Image:24-06-52.jpg]]. Прямая с, пересекающая данные параллельные прямые, имеет с плоскостью а две общие точки — точки пересечения с данными прямыми. По теореме 15.2 эта прямая лежит в плоскости [[Image:24-06-52.jpg]]. Итак, все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости — плоскости [[Image:24-06-52.jpg]]. | | Решение. Так как данные прямые а и b параллельны, то через них можно провести плоскость (рис. 323). Обозначим ее [[Image:24-06-52.jpg]]. Прямая с, пересекающая данные параллельные прямые, имеет с плоскостью а две общие точки — точки пересечения с данными прямыми. По теореме 15.2 эта прямая лежит в плоскости [[Image:24-06-52.jpg]]. Итак, все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости — плоскости [[Image:24-06-52.jpg]]. |
| | | | |
| - | Теорема 16.1.'''''Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.''''' | + | '''Теорема 16.1. '''Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну. |
| | | | |
| | Замечание. Утверждение единственности в теореме 16.1 не является простым следствием аксиомы параллельных, так как этой аксиомой утверждается единственность прямой, параллельной данной в данной плоскости. Поэтому она требует доказательства. | | Замечание. Утверждение единственности в теореме 16.1 не является простым следствием аксиомы параллельных, так как этой аксиомой утверждается единственность прямой, параллельной данной в данной плоскости. Поэтому она требует доказательства. |
| Строка 19: |
Строка 19: |
| | <br> | | <br> |
| | | | |
| - | [[Image:30-06-2.jpg]] | + | [[Image:30-06-2.jpg|240px| Параллельные прямые]] |
| | | | |
| | <br> | | <br> |
| Строка 31: |
Строка 31: |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <sub>Школьная библиотека [[Гипермаркет знаний - первый в мире!|онлайн]], учебники и книги по всему предметам, Математика 10 класс [[Математика|скачать]]</sub> | + | <br> <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> <br> |
| - | | + | |
| - | <br> | + | |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Решение. Так как данные прямые а и b параллельны, то через них можно провести плоскость (рис. 323). Обозначим ее  . Прямая с, пересекающая данные параллельные прямые, имеет с плоскостью а две общие точки — точки пересечения с данными прямыми. По теореме 15.2 эта прямая лежит в плоскости
. Прямая с, пересекающая данные параллельные прямые, имеет с плоскостью а две общие точки — точки пересечения с данными прямыми. По теореме 15.2 эта прямая лежит в плоскости  . Итак, все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости — плоскости
. Итак, все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости — плоскости  .
.
Замечание. Утверждение единственности в теореме 16.1 не является простым следствием аксиомы параллельных, так как этой аксиомой утверждается единственность прямой, параллельной данной в данной плоскости. Поэтому она требует доказательства.
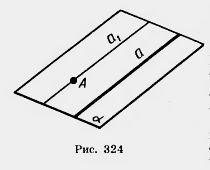
Доказательство. Пусть a — данная прямая и А —точка, не лежащая на этой прямой (рис. 324). Проведем через прямую а и точку А плоскость  . Проведем через точку А в плоскости
. Проведем через точку А в плоскости  прямую a1, параллельную a. Докажем, что прямая a1, параллельная a, единственна.
прямую a1, параллельную a. Докажем, что прямая a1, параллельная a, единственна.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.