Версия 20:20, 31 августа 2015

Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Основные тригонометрические тождества. Полные уроки

Тема урока

Основные тригонометрические тождества.

Цели урока

• Углубить знания по истории геометрии.
• Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
• Сформулировать и доказать свойства квадрата, доказать его свойства.
• Научиться применять свойства фигур при решении задач.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные - посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока

• Проверить умение учащихся решать задачи.

План урока

1. Историческая справка.
2. Повторение материала по теме.
3. Основные тригонометрические тождества.

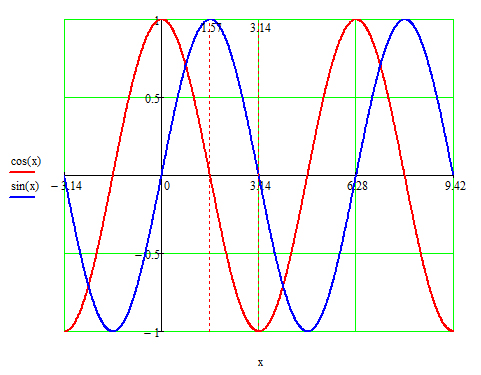
Историческая справка

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников.

В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.

Возникновение  тригонометрии связано с землемерением, астрономией и строительным делом.

Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.

Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский  астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Аль-Батани

Абу-ль-Вафа

Насиреддин Туси Мухамед

Бхаскара

Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия.  Современный синус, например, изучался как полухорда, на которую опирается центральный угол величиной, или как хорда удвоенной дуги.

Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”).
Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов.  Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.

Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г.  Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).

Повторение материала по теме: "Тригонометрия и тригонометрические функции"

Тригонометрия - это такое сложное греческое слово: тригонон - треугольник, метро - мерять. Стало быть по-гречески это означает: меряться треугольниками. Очень странное слово. Может быть древнегреки под треугольниками подразумевали кое-что другое? Не знаю.

Тригонометрические функции — вид элементарных функций, изучаемых в тригонометрии. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна. В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.

Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса

Определение тригонометрических функций для острых углов

Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α.

Тогда:

• Синусом называется отношение AB/OB (отношение противолежащего катета к гипотенузе)
• Косинусом называется отношение ОА/OB (отношение прилежащего катета к гипотенузе)
• Тангенсом называется отношение AB/OA (отношение противолежащего катета к прилежащему)
• Котангенсом называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
• Секансом называется отношение ОB/OA (отношение гипотенузы к прилежащему катету)Косекансом α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету)

Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.

Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники

Научиться применять основные тригонометрические формулы очень важная задача. Именно эти формулы будут чаще всего являться ключом к решению тех или иных примеров по тригонометрии.

Основные тригонометрические тождества

Основные тригонометрические соотношения связаны тождествами:

1. tg a = sin a /cos a
2. sin² a + cos² a = 1
3. 1 + tg² a = 1/cos² a
4. 1 + 1/tg² a = 1/sin² a
5. sin(90^o– a ) = cos a
6. cos(90^o– a ) = sin a    

Тождество №1

Первая формула говорит о то что если знаете синус или косинус числа, то Вы можете найти его тангенс или котангенс (котангенс - обратная функция тангенса).

Отсюда следует, что произведение тангенса и котангенса равно единице.

Тождество №2

В этой части речь идет о соотношении косинуса и синуса одинаковых численных значений. Эта формула позволяет найти синус числа, если известен его косинус, и найти косинус числа, если известен его синус.

Тождество №3

Если вовремя расчетов есть потребность тангенс когда известен косинус - это можно реализовать если сначала найти синус. Но обратный путь намного сложнее. Что бы облегчить работу формула которая позволяет это сделать уже выведена, она позволяет оба этих пути проходить сразу.

Обратите внимание на значение какие не может принимать альфа.

Тождество №4

Четвертое тождество, аналогично третьему, только вместо тангенса используется котангенс и вместо косинуса - синус.

Как и в прошлом тождестве обратите внимание на значение какие не может принимать альфа, оно отличается от предыдущего.

Тождество №5, 6

Последние два тождества доказываются просто.

Из за того что функция косинус опережает синус на 90 градусов возникло такое тождество.

На графике видно то что разница между функциями равно 90 градусов.

Формулы приведения

Интересные факты

Двоичная система счисления.

Сложность цивилизации, как в зеркале отражается в сложности используемых ею чисел. Две с половиной тысячи лет назад вавилоняне довольствовались натуральными числами, подсчитывая принадлежащие им несколько овец, сегодня экономисты пользуются метрической алгеброй для описания взаимосвязей сотен предприятий.

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (1 и 0).

Двоичный код это форма записи данных в виде нулей и единиц. Запись чисел в двоичной системе счисления называется двоичным кодом. Двоичная система счисления это позиционная система счисления с основанием два. Двоичный код применяется во всех цифровых устройствах т.к. является самым простым и надежным. Двоичная арифметика очень простая и ее просто реализовать на аппаратном уровне. Элементы электронных схем, надежнее, если они оперируют терминами «есть ток», «нет тока».

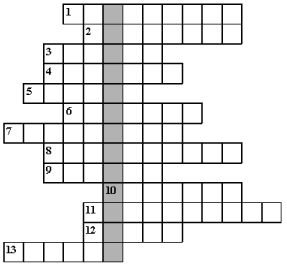
Это интересно знать

А знали ли вы о таком интересном факте, что математики Древней Греции выполняя построения, где нужно было измерить дуги круга, применяли технику хорд. Ведь вы уже изучали этот материал и знаете, что опущенный из центра окружности перпендикуляр к хорде, делит пополам дугу и хорду, которая на нее опирается. А так как половина поделенной пополам хорды является синусом поделенного угла, то такую функцию, как синус, еще называют половиной хорды. Вот такая у нас образовалась зависимость. Но благодаря этой зависимости известные в настоящее время тригонометрические тождества, а также и теоремы, использовали и математики Древней Греции, но, правда, они ее использовали в эквивалентной хордовой форме.

Известен ли вам тот факт, что главным достижением математиков Индии в Средние века была замена хорд на синусы? С помощью такой уникальной замены мудрецы Индии могли вводить различные функции, которые имели отношение к сторонам и углам прямоугольного треугольника. Поэтому, можно смело говорить, что в этой стране зародилась тригонометрия, как наука об учении, о тригонометрических величинах.

А знаете ли вы о том, как тригонометрия дошла до наших дней? Оказывается, что с трудами математиков и астрономов Индии познакомились ученые Востока и перевели их вначале на арабский язык, а после того, как перевод был сделан на латыни, то об этих важных открытиях стало известно и европейским ученым, а со временем и всей мировой науке.

А хотите узнать, как можно легко запомнить основное тригонометрическое тождество методом эдейтики, то есть с помощью конкретно-образного мышления? Вот такой интересный пример для быстрого запоминания придумала преподаватель общей математики Луганского Национального Университета О.В. Панишева:

Домашнее задание

Вы уже знаете, что такое тригонометрия, косинус, синус, тангенс и какие функции они выполняют, поэтому для вас не составит труда решить кроссворд:

1. Какое название носит кофункция тангенса?
2. То от чего может зависеть значение функции.
3. Назовите меру измерения угла.
4. Перед вами функции: sin x, cos x, ctg x... Какой функции в этом перечне нехватает?
5. Назовите обозначение, через которое повторяется значение тригонометрических функций.
6. Чем является cos x?
7. Как называется график функции sin x?
8. (0; p) – дайте название этому обозначению.
9. Он бывает и в земле, и в математике.
10. Какое название носит предложение, которое требует доказательства?
11. Как называется число из отрезка [0; p], у которого косинус равен a?
12. Как называется отношение противолежащего катета к гипотенузе.
13. Если sin x является нечетной функцией, то cos x является …. функцией.