Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Введение декартовых координат в пространстве

Введение декартовых координат в пространстве

Возьмем три взаимно перпендикулярные прямые х, у, z, пересекающиеся в одной точке О (рис. 378). Проведем через каждую пару этих прямых плоскость.

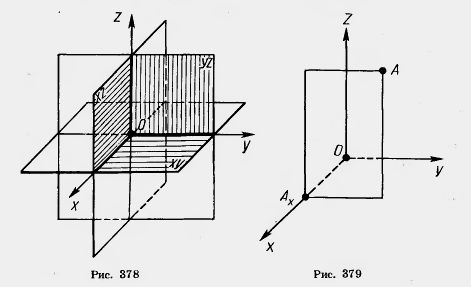
Плоскость, проходящая через прямые x и y, называется плоскостью ху. Две другие плоскости называются соответственно xz и yz. Прямые х, у, z называются координатными осями (или осями координат), точка их пересечения О — началом координат, а плоскости ху, yz и xz — координатными плоскостями. Точка О разбивает каждую из осей координат на две полупрямые — полуоси, которые мы условимся называть положительной и отрицательной.

Возьмем теперь произвольную точку А и проведем через нее плоскость, параллельную плоскости yz (рис. 379). Она пересекает ось X в некоторой точке А_x.

Координатой х точки А будем называть число, равное по абсолютной величине длине отрезка ОА_x положительное, если точка А_x лежит на положительной полуоси X, и отрицательное, если она лежит на отрицательной полуоси. Если точка Ах совпадает с точкой О, то полагаем x = 0. Аналогично определяются координаты у и z точки А. Координаты точки будем записывать в скобках рядом с буквенным обозначением точки: А (х; у; z). Иногда будем обозначать точку просто ее координатами (х; у; z).

 
Задача (2). Даны точки А (1; 2; 3), В(0; 1; 2), С(0; 0; 3), D(l; 2; 0). Какие из этих точек лежат:

1) в плоскости ху;

2) на оси z;

3) в плоскости yz?

Решение. У точек плоскости ху координата z равна нулю. Поэтому только точка D лежит в плоскости ху. У точек плоскости yz координата х равна нулю. Следовательно, точки В и С лежат в плоскости yz. У точек на оси Z две координаты (х и у) равны нулю. Поэтому только точка С лежит на оси z.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.