|
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Вращательное движение твердого тела. Угловая и линейная скорости вращения
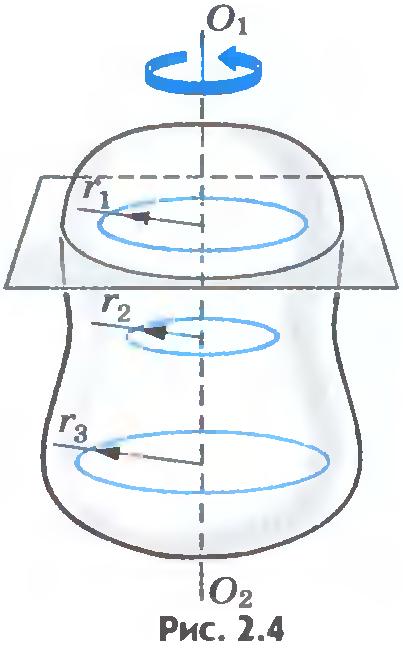
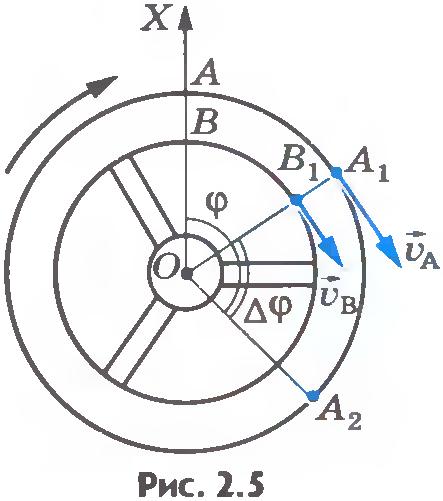
Вращательное движение вокруг неподвижной оси - еще один частный случай движения твердого тела. Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения (рис.2.4). В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолетов. Угловая скорость. Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и различные точки проходят за время Пусть тело вращается равномерно, т. е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению Угловая скорость выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси равна 0,0000727 рад/с, а точильного диска - около 140 рад/с1. Угловую скорость можно выразить через частоту вращения, т. е. число полных оборотов за 1с. Если тело совершает Полному обороту тела соответствует угол Если при равномерном вращении угловая скорость известна и в начальный момент времени Если Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательные, когда он уменьшается. Тем самым мы можем описать положение точек вращающегося тела в любой момент времени. Связь между линейной и угловой скоростями. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости. Мы уже отмечали, что при вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова. Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь Так как Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Для точек земного экватора Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности: Следовательно, Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет. Итак, мы научились полностью описывать движение абсолютно твердого тела, вращающегося равномерно вокруг неподвижной оси, так как, пользуясь формулами ??? 1. Что называется осью вращения твердого тела? 2. Что такое угловая скорость? 3. Во сколько раз угловая скорость минутной стрелки часов больше угловой скорости часовой стрелки?
Содержание урока Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: