Гипермаркет знаний>>Математика>>Математика 10 класс>> Как построить график функции у=mf(x), если известен график функции y = f(x)

Как построить график функции у=mf(x), если известен график функции y = f(x)

В курсе алгебры 8-го класса мы обсудили вопрос о том, как, зная график функции у = f(x), можно построить графики функций у = f(х + а), у = f(х) + Ь,у = f(х + а) + b. Оказалось, что все эти графики получаются из графика функции у = f(х) с помощью преобразования параллельного переноса (на | а | единиц масштаба вправо или влево вдоль оси х и на | B | единиц масштаба вверх или вниз вдоль оси у). В предыдущих параграфах мы осуществляли эти преобразования для графиков степенных функций. Теперь познакомимся еще с одним преобразованием, позволяющим, зная график функции у = Дх), довольно быстро строить график функции у = mf(х), где m — любое действительное число.

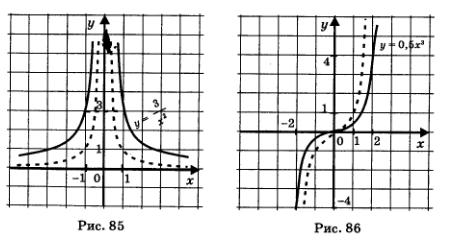
Первый случай. Зная график функции у = f(х), построить график функции у = mf(х), где m — положительное число.

Ординаты точек графика функции у = mf(х) получаются в результате умножения соответствующих ординат точек графика функции у = f(х) на число m. Такое преобразование графика называют обычно растяжением от оси х с коэффициентом m. Заметим, что при этом преобразовании остаются на месте точки пересечения графика функции у = f(х) с осью х (т.е. точки, удовлетворяющие уравнению f(х) = 0).

Впрочем, если m < 1, то предпочитают использовать другой термин: не растяжение с коэффициентом m, а сжатие к оси х с коэффициентом — (если то говорят не о растяжении с коэффициентом а о сжатии с коэффициентом 3).

На рис. 85 изображены графики функций (пунктиром)

Второй случай.Зная график функции у = f(х), построить график функции у = mf(х), где m = -1. Иными словами, речь идет о построении графика функции у = -f(х).

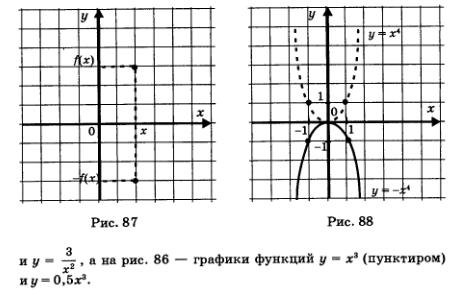
Ординаты точек графика функции у = -f(х) отличаются от соответствующих ординат точек графика функции у = f(х) только знаком. Точки (х; f(х)) и (х; -f(х)) симметричны относительно оси х (рис. 87). Значит, график функции у = -f(х) можно получить из графика функции у — f(х) с помощью преобразования симметрии относительно оси х. На рис. 88 изображены графики функций у = х⁴ и у = -х⁴.

Третий случай. Зная график функции у = f(х), построить график функции у = mf(х), где m — отрицательное число.
Так как в этом случае справедливо равенство mf(х) = -1 m | f(х), то речь идет о построении графика функции у = -1 m ] f(х). Это можно сделать в три шага:

1)    построить график функции у = f(х);
2)    растянуть его от оси х с коэффициентом | m |;
3)    растянутый график подвергнуть преобразованию симметрии относительно оси х.
Пример. Построить график функции
Решение. 1) Построим график функции (пунктирная линия на рис. 89).
2)    Осуществим растяжение построенного графика от оси х с коэффициентом 2 (сплошная черная линия на рис. 89); получим график функции
3)    Подвергнув график функции преобразованию симметрии относительно оси х, получим график функции   (цветная линия на рис. 89).

А.Г. Мордкович Алгебра 10 класс

_{Видеопо математике скачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.