|
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Как построить график функции у = mf(x), если известен график функции у = f(x)
Как построить график функции у = mf(x), если известен график функции у = f(x)
В курсе алгебры 8-го класса мы обсудили вопрос о том, как, зная график функции у = f(x), можно построить графики функций у = f(х + а), у = f(х) + Ь,у = f(х + а) + b. Оказалось, что все эти графики получаются из графика функции у = f(х) с помощью преобразования параллельного переноса (на | а | единиц масштаба вправо или влево вдоль оси х и на | B | единиц масштаба вверх или вниз вдоль оси у). В предыдущих параграфах мы осуществляли эти преобразования для графиков степенных функций. Теперь познакомимся еще с одним преобразованием, позволяющим, зная график функции у = Дх), довольно быстро строить график функции у = mf(х), где m — любое действительное число.
Первый случай.
Зная график функции у = f(х), построить график функции у = mf(х), где m — положительное число.
Ординаты точек графика функции у = mf(х) получаются в результате умножения соответствующих ординат точек графика функции у = f(х) на число m. Такое преобразование графика называют обычно растяжением от оси х с коэффициентом m. Заметим, что при этом преобразовании остаются на месте точки пересечения графика функции у = f(х) с осью х (т.е. точки, удовлетворяющие уравнению f(х) = 0).
Впрочем, если m < 1, то предпочитают использовать другой термин: не растяжение с коэффициентом m, а сжатие к оси х с коэффициентом — (если 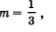 то говорят не о растяжении с коэффициентом то говорят не о растяжении с коэффициентом 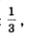 а о сжатии с коэффициентом 3). а о сжатии с коэффициентом 3).
На рис. 85 изображены графики функций 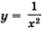 (пунктиром) (пунктиром)
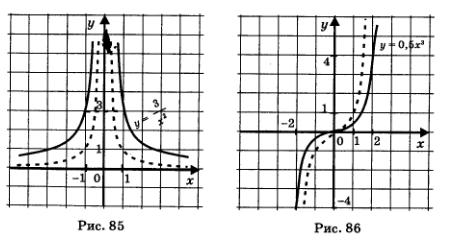
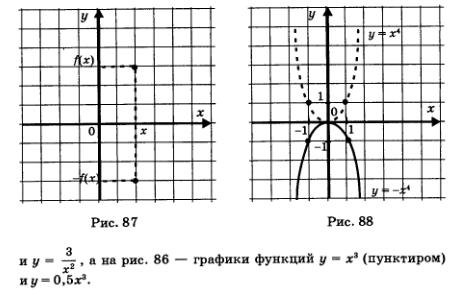
Второй случай.
Зная график функции у = f(х), построить график функции у = mf(х), где m = -1. Иными словами, речь идет о построении графика функции у = -f(х).
Ординаты точек графика функции у = -f(х) отличаются от соответствующих ординат точек графика функции у = f(х) только знаком. Точки (х; f(х)) и (х; -f(х)) симметричны относительно оси х (рис. 87). Значит, график функции у = -f(х) можно получить из графика функции у — f(х) с помощью преобразования симметрии относительно оси х. На рис. 88 изображены графики функций у = х4 и у = -х4.
Третий случай.
Зная график функции у = f(х), построить график функции у = mf(х), где m — отрицательное число.
Так как в этом случае справедливо равенство mf(х) = -1 m | f(х), то речь идет о построении графика функции у = -1 m ] f(х). Это можно сделать в три шага:
1) построить график функции у = f(х);
2) растянуть его от оси х с коэффициентом | m |;
3) растянутый график подвергнуть преобразованию симметрии относительно оси х.
Пример.
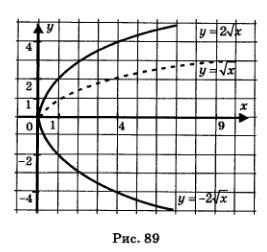
Построить график функции 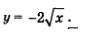
Решение.
1) Построим график функции 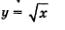 (пунктирная линия на рис. 89). (пунктирная линия на рис. 89).
2) Осуществим растяжение построенного графика от оси х с коэффициентом 2 (сплошная черная линия на рис. 89); получим график функции 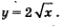
3)Подвергнув график функции 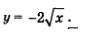 преобразованию симметрии относительно оси х, получим график функции преобразованию симметрии относительно оси х, получим график функции 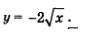 (цветная линия на рис. 89). (цветная линия на рис. 89).
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













