Гипермаркет знаний>>Математика>>Математика 11 класс>> Математика:Пирамида

Конспект урока к предмету Математика 11 класс

Тема

Пирамида

Ход урока

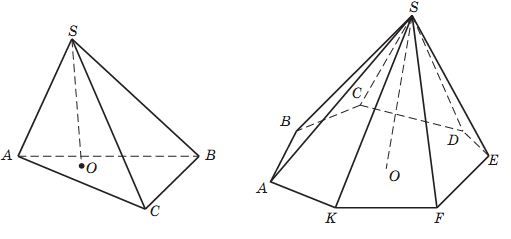
Цель

• Продолжать расширять знания о многогранниках;
• Сформировать знания учеников о понятии пирамида;
• Расширить сведения о пирамидах, ее площади поверхности и объеме.
• Научить школьников находить элементы этой фигуры.

Задачи

• Продолжать пополнять знания детей о многогранных фигурах;
• Вызвать познавательный интерес учеников к предмету геометрии;
• Развивать у школьников пространственное воображение;
• Воспитывать волевые качества школьников и целеустремленность.

Вступление

У многих из вас при слове пирамида возникают ассоциации, связанные с египетскими пирамидами. В архитектурных постройках такая форма используется довольно часто, но сейчас мы поговорим об этой многогранной фигуре, с точки зрения геометрии.

Пирамида - это такой многогранник, состоящий из многоугольника, который имеет плоскую форму и точку, не лежащую на этой плоскости, но соединяющуюся с точками многоугольника, лежащего на плоскости.

Многоугольник является основой этой многогранной фигуры, а нележащая на поверхности плоскости точка, называется ее вершиной. Отрезки, участвующие в соединении ее вершины с вершиной основания носят название боковых ребер.

Из всего выше сказанного можно сделать вывод, что поверхность любой пирамиды состоит из основания и боковых граней. Каждая такая грань имеет форму треугольника.

Многогранная фигура и ее плoщадь

А теперь узнаем, чему равна плoщадь пирамиды. Если рассматривать плoщадь ее бoковой пoверхности, то она равняется сумме площадей боковых граней. А чтобы узнать полную плoщадь поверхности, то нужно приплюсовать площади оснoвания и бокoвой пoверхности пирамиды.

Высотой этого многогранника является перпендикуляр, опущенный с вершины на основание поверхности.

Если в основе многогранной фигуры расположен n-угольник, то такая пирамида носит название n-угольной.

Тетраэдром называют многогранник треугольной формы.

Если же ее основание имеет правильную форму многоугольника и совпадает с его центром, то такая пирамида носит название правильной.

Прямая, которая содержит высоту пирамиды, носит название оси правильной пирамиды.

А проведенная линия с высоты вершины боковой грани называется апофемой.

Изображение на плоскости

Для изображения этой многогранной фигуры на плоскости необходимо:

• Во-первых, построить многоугольник в основании пирамиды;
• Во-вторых, отметить и изобразить ее высоту;
• В-третьих, соединить отрезками вершину данной фигуры с вершинами многоугольника, который лежит у основания.

Задание

• Что называется осью многогранной фигуры?
• Что такое апофема? Дайте определение.
• Назовите известные вам свойства правильной пирамиды.
• Дайте определение ее площади объема?
• Что мы получим в результате, если основу тетраэдра поменять из треугольника на четырехугольник?

Домашнее задание

Внимательно прочитайте текст и решите задачи:

• Вычислите апофему пирамиды, если площадь боковых граней 4-х угольного многогранника равна 60 см2, а периметр основания равен 15 см.

• Чему равняется высота фигуры, если ее основанием является прямоугольный треугольник, у которого катеты 8 см и 10 см, а боковые ребра 15 см?