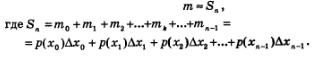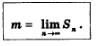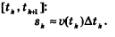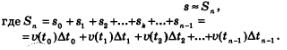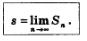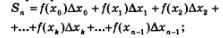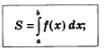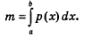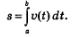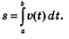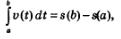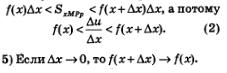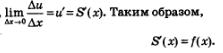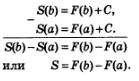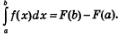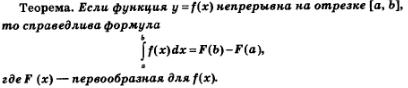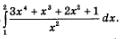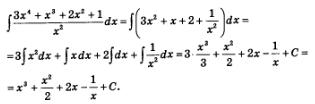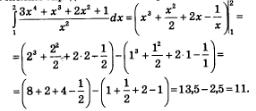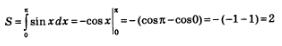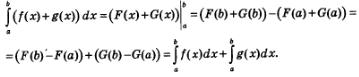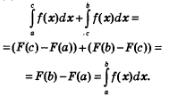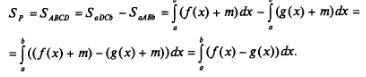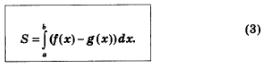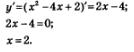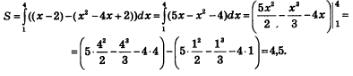|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Определенный интеграл
§ 38. Определенный интеграл
1. Задачи, приводящие к понятию определенного интеграла
Задача 1 (о вычислении площади криволинейной трапеции).
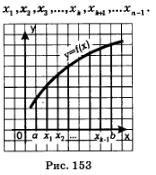
В декартовой прямоугольной системе координат хОу дана фигура (рис. 153), ограниченная осью х, прямыми х=а,х=Ь (а <Ъ) и графиком непрерывной и неотрицательной на отрезке [а, Ь] функции у = f(х); назовем эту фигуру криволинейной трапецией. Требуется вычислить площадь криволинейной трапеции.
Решение. Геометрия дает нам рецепты для вычисления площадей многоугольников и некоторых частей круга (сектор, сегмент). Используя геометрические соображения, мы сумеем найти лишь приближенное значение искомой площади, рассуждая следующим образом.
Разобьем отрезок [а, Ь] (основание криволинейной трапеции) на п равных частей; это разбиение осуществим с помощью точек
Проведем соответствующие ординаты. Тогда заданная криволинейная трапеция разобьется на n частей — на n узеньких столбиков. Площадь всей трапеции равна сумме площадей столбиков.
Рассмотрим отдельно k-тый столбик, т.е. криволинейную трапецию, основанием которой служит отрезок 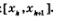 Заменим его прямоугольником с тем же основанием и высотой, равной f(хк) (рис. 154). Площадь прямоугольника равна Заменим его прямоугольником с тем же основанием и высотой, равной f(хк) (рис. 154). Площадь прямоугольника равна 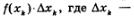 — длина отрезка — длина отрезка 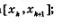 ; естественно считать составленное произведение приближенным значением площади к-то столбика. ; естественно считать составленное произведение приближенным значением площади к-то столбика.
Если теперь сделать то же самое со всеми остальными столбиками, то придем к следующему результату: площадь 5 заданной криволинейной трапеции приближенно равна площади 5. ступенчатой фигуры, составленной из п прямоугольников (рис. 155). Имеем:
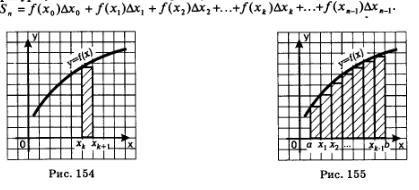
Здесь ради единообразия обозначений мы считаем, что
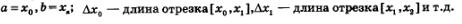
Итак, S = Sn, причем это приближенное равенство тем точнее, чем больше п.
Принято считать, что искомая площадь есть предел последовательности 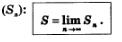
Задача 2 (о вычислении массы стержня).
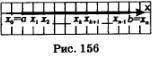
Дан прямолинейный неоднородный стержень (рис. 156), плотность в точке х вычисляется по формуле р=р(х). Найти массу стержня.
Решение. Масса тела, как известно из курса физики, равна произведению плотности на объем (вместо объема берут площадь — если речь идет о плоской пластине; вместо объема берут длину — если речь идет о прямолинейном стержне без учета его толщины). Но этот закон действует только для однородных тел, т.е. в тех случаях, когда плотность постоянна. Для неоднородного стержня используется тот же метод, что был применен при решении задачи 1.
1) Разобьем отрезок [а, Ь] на п равных частей.
2) Рассмотрим k-тый участок 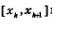 и будем считать, что плотность во всех точках этого участка постоянна, а именно такая, как, например, в точке хк. Итак, мы считаем, что р = р (хк). и будем считать, что плотность во всех точках этого участка постоянна, а именно такая, как, например, в точке хк. Итак, мы считаем, что р = р (хк).
3) Найдем приближенное значение массы mк к-то участка: 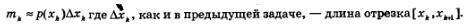
4) Найдем приближенное значение массы m стержня:
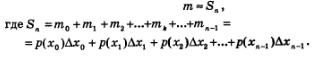
5) Точное значение массы стержня вычисляется по формуле
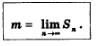
Задача 3 (о перемещении точки).
По прямой движется материальная точка. Зависимость скорости от времени выражается формулой v = v(t); пусть для определенности t>(f) >0. Найти перемещение точки за промежуток времени [а, Ь].
Решение. Ее ли бы движение было равномерным, то задача решалась бы очень просто: 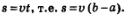 Для неравномерного движения приходится использовать те же идеи, на которых было основано решение двух предыдущих задач. Для неравномерного движения приходится использовать те же идеи, на которых было основано решение двух предыдущих задач.
1) Разделим промежуток времени [а, Ь] на п равных частей.
2) Рассмотрим промежуток времени 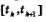 и будем считать, что в этот промежуток времени скорость была постоянной, такой, как в момент времени. Итак, мы считаем, что v = v (t4). и будем считать, что в этот промежуток времени скорость была постоянной, такой, как в момент времени. Итак, мы считаем, что v = v (t4).
3) Найдем приближенное значение перемещения точки зк за промежуток времени
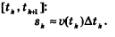
4) Найдем приближенное значение перемещения з:
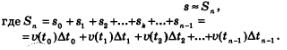
5) Точное значение перемещения вычисляется по формуле 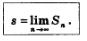
Подведем итоги. Три различные задачи привели при их решении к одной и той же математической модели. Многие задачи из различных областей науки и техники приводят в процессе решения к такой же модели. Значит, данную математическую модель надо специально изучить, т.е.:
а) присвоить ей новый термин,
б) ввести для нее обозначение,
в) научиться с ней работать.
Этим и займемся.
2. Понятие определенного интеграла
Дадим математическое описание той модели, которая была построена в трех рассмотренных задачах для функции у = f(х), непрерывной (но необязательно неотрицательной, как это предполагалось в рассмотренных задачах) на отрезке [а, Ь]:
1) разбивают отрезок [а, Ь] на n равных частей;
2) составляют сумму:
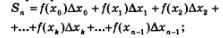
3) вычисляют 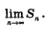
В курсе математического анализа доказано, что при указанных условиях этот предел существует. Его называют определенным интегралом от функции у =f(x) по отрезку [а, Ь] и обозначают так:
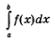
(читают: «интеграл от а до Ь эф от икс дз икс»). Числа а и Ь называют пределами интегрирования (соответственно нижним и верхним).
Замечание. Приведем правдоподобную версию происхождения указанного обозначения и термина: 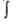 — стилизованная буква — стилизованная буква 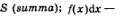 напоминание о слагаемых вида напоминание о слагаемых вида 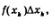 из которых состоит сумма 5д. Само слово интеграл происходит от латинского слова integer — «целый». Употребление этого термина вполне оправданно: вспомните, какой смысл вкладывается в русском языке в слово интеграция — восстановление, восполнение, воссоединение; подробнее — это процесс, ведущий к состоянию связанности отдельных частей в целое. В построенной математической модели речь фактически идет о воссоединении целого по отдельным частям (например, о нахождении всей площади — по площадям столбиков, как было в задаче 1). из которых состоит сумма 5д. Само слово интеграл происходит от латинского слова integer — «целый». Употребление этого термина вполне оправданно: вспомните, какой смысл вкладывается в русском языке в слово интеграция — восстановление, восполнение, воссоединение; подробнее — это процесс, ведущий к состоянию связанности отдельных частей в целое. В построенной математической модели речь фактически идет о воссоединении целого по отдельным частям (например, о нахождении всей площади — по площадям столбиков, как было в задаче 1).
Вернемся к трем рассмотренным выше задачам. Результат, полученный в задаче 1, теперь можно переписать следующим образом:
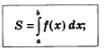
здесь S — площадь криволинейной трапеции, изображенной на рис. 153. В этом состоит геометрический смысл определенного интеграла.
Из решения задачи 2 следует, что масса m неоднородного стержня с плотностью р(х) вычисляется по формуле
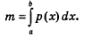
В этом состоит физический смысл определенного интеграла.
Из решения задачи 3 следует, что перемещение з точки, движущейся по прямой со скоростью v = v(t), за промежуток времени от t =а до 1 = Ъ, вычисляется по формуле
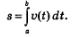
Это — еще одно физическое истолкование определенного интеграла.
3. Формула Ньютона—Лейбница
После внимательного изучения предыдущего параграфа у вас, наверное, возник вопрос: почему в названии построенной математической модели содержится слово «интеграл», ведь в § 37 это слово ассоциировалось у нас с термином «первообразная». Есть ли какая-либо связь между определенным интегралом и первообразной?
Ключ к разгадке дает задача 3. С одной стороны, перемещение 8 точки, движущейся по прямой со скоростью v=v(t), за промежуток времени от t=a до t =Ь вычисляется по формуле
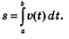
С другой стороны, координата движущейся точки есть первообразная для скорости — обозначим ее s (t); значит, перемещение S выражается формулой S = s(b) -S(а). В итоге получаем:
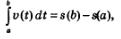
где S (t) — первообразная для v(t).
Вернемся к задаче 1 — о вычислении площади криволинейной трапеции (см. рис. 153). Мы установили, что

Сейчас мы покажем другое решение этой задачи, которое приведет нас к формуле
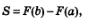
где F (х) — первообразная для f(х). Будем считать для упрощения, что у = f(х) — возрастающая функция на отрезке [а, Ь).
Выберем между а и Ь на оси абсцисс фиксированную точку х и рассмотрим криволинейную трапецию аАМх (рис. 157), обозначим ее площадь через 5 (х). Каждому х из отрезка [а, Ь] соответствует вполне определенное значение S(х), т.е. можно говорить о функции u = S(х). Эта функция определена на отрезке [а, Ь], она неотрицательна и возрастает (чем больше х, тем большую площадь имеет криволинейная трапеция аАМх).
Особо отметим значения функции на концах отрезка [а, b]:
если х=а, то трапеция аАМх «вырождается» в отрезок аА, его площадь равна нулю, т.е. S(а) =0;
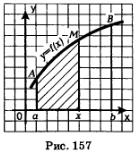
если а = Ь, то трапеция аАМх совпадает с трапецией аAВЬ, площадь 5 которой нам как раз и надо вычислить, т.е. S(Ь) =5.
Вся подготовительная работа закончена, приступим к решению задачи о вычислении площади криволинейной трапеции аАВЬ. Осуществим это решение в два этапа.
Первыйэтап. Найдем производную функции u =S(х), применив выработанный в § 32 алгоритм.
1) Для фиксированного значения х имеем: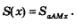
2) Дадим аргументу приращение 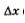 (пусть для определенности выполняется неравенство (пусть для определенности выполняется неравенство 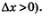 ). Для значения ). Для значения 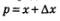 имеем (рис. 158) имеем (рис. 158)
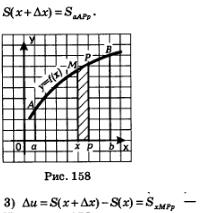
площадь узенького столбика хМРр на рис. 158.
4) Функция у=f(х) возрастает на отрезке 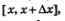 значит, f(х) — наименьшее значение функции на указанном отрезке, а значит, f(х) — наименьшее значение функции на указанном отрезке, а 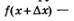 — наибольшее значение функции на указанном отрезке. Но тогда — наибольшее значение функции на указанном отрезке. Но тогда
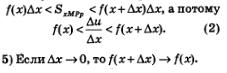
Анализируя неравенство (2), логично предположить, что тогда 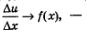 в курсе математического анализа доказано, что это верно. Но, как известно, в курсе математического анализа доказано, что это верно. Но, как известно,
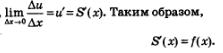
иными словами, S (х) — первообразная для f(х).
Второй зтап. Имеем: S(Ь) = S; S (а) = 0, значит, S = S(b)-S(а).
Приступая к решению задачи, мы для функции f(х) выбрали первообразную F(х). Значит, теперь у нас есть две первообразные для f(х): F(х) и S (х). Они, как известно, отличаются друг от друга на постоянную величину, т.е.
S(х)=F(х)+С.
Далее имеем:
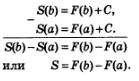
Сопоставив этот результат с формулой (1), получим:
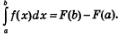
Вообще, в курсе математического анализа доказана следующая теорема.
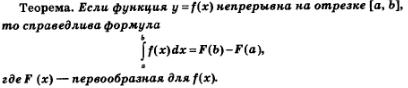
Приведенную формулу обычно называют формулой Ньютона—Лейбница в честь английского физика Исаака Ньютона (1643—1727) и немецкого философа Готфрида Лейбница (1646—1716), получивших ее независимо друг от друга и практически одновременно.
Замечание. То, что математическую формулу вывели философ и физик, никого не удивляет, ведь математика — язык, на котором говорит сама природа.
На практике вместо записи F(Ь)-F(а) используют запись 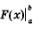 (ее называют иногда двойной подстановкой) и соответственно переписывают формулу Ньютона—Лейбница в виде: (ее называют иногда двойной подстановкой) и соответственно переписывают формулу Ньютона—Лейбница в виде:
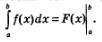
Вычисляя определенный интеграл, сначала находят первообразную, а затем осуществляют двойную подстановку.
Пример 1. Вычислить 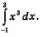
Решение. Первообразной для х3 служит 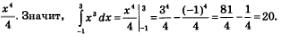
Пример 2. Вычислить 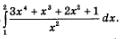
Решение. Здесь для отыскания первообразной удобнее воспользоваться знаком неопределенного интеграла, при этом полезно числитель дроби, содержащейся под знаком интеграла, разделить почленно на ее знаменатель:
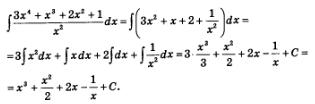
Теперь вычислим определенный интеграл:
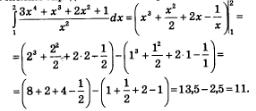
Пример 3. Вычислить площадь фигуры, ограниченной одной полуволной синусоиды у = sin х и осью абсцисс.
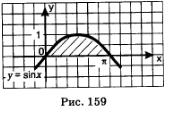
Решение. Можно взять полуволну синусоиды от точки х = 0 до точки х = к (рис. 159) и воспользоваться формулой (1) при следующих условиях: а = О, Ь = п, f(x) = sin х. Получим:
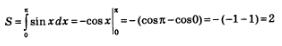
(в процессе вычислений мы учли, что первообразной для sin x является -соs x:).
Ответ: S=2.
Опираясь на формулу Ньютона—Лейбница, нетрудно обосновать некоторые свойства определенного интеграла.
Свойство 1. Интеграл от суммы функций равен сумме интегралов:
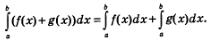
Доказательство. Если F(х) — первообразная для f(х), а G(x) — первообразная для g(х), то f(х)+G(x) — первообразная для f(х)+g(х). Тогда:
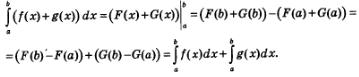
Свойство 2. Постоянный множитель можно вынести за знак интеграла:
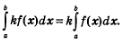
Свойство 3. Если а < с < Ь, то
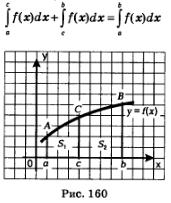
{аддитивное свойство интеграла).
Доказательство.
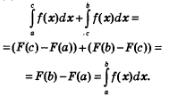
Геометрический смысл аддитивного свойства интеграла заключается в том, что (см. рис. 160) площадь криволинейной трапеции равна сумме площадей криволинейных трапеций, из которых она составлена:
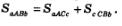
4. Вычисление площадей плоских фигур с помощью определенного интеграла
С помощью интеграла можно вычислить площади не только криволинейных трапеций того вида, который представлен на рис. 160, но и плоских фигур более сложного вида, например, такого, который представлен на рис. 161. Фигура F (рис. 161а) ограничена прямыми x =а, и графиками непрерывных функций у = f(х), у = g(х), причем на отрезке [а, Ь] выполняется неравенство g(х)<f(х). Для вычисления площади такой фигуры будем рассуждать следующим образом.
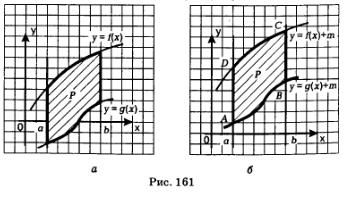
Выполним параллельный перенос фигуры Р на т единиц вверх (m > 0) так, чтобы фигура Р оказалась расположенной в координатной плоскости выше оси абсцисс (рис. 161 б). Теперь она ограничена сверху и снизу графиками функций у = f(х)+m, у = g(х)+m, причем обе функции непрерывны и неотрицательны на отрезке [а, Ь]. Имеем:
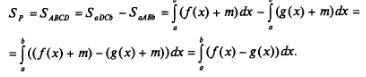
Итак, площадь S фигуры, ограниченной прямыми х = а, х = Ь и графиками функций у = f(х)>v = S(х)> непрерывных на отрезке [а, Ь] и таких, что g(х)<f(х)длявсеххиз отрезка [а, Ь], вычисляется по формуле
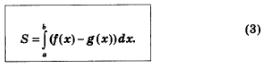
Пример 4. Вычислить площадь фигуры, ограниченной линиями у = х,у = Ъ- х, x = 1, х = 2.
Решение. Фигура, площадь которой надо найти, изображена на рис. 162. Воспользовавшись формулой (3), получим:
Пример 5. Вычислить площадь фигуры, ограниченной прямой у-х-2 и параболой у = x2 -4x + 2.
Решение. Прямую у = х-2 можно построить по точкам (2; 0) и (0; -2) (рис. 163). Абсциссу вершины параболы найдем из условия у'=0. Имеем:
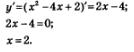
Если x = 2, то у = 22 -4-2 +2 = -2. Значит, вершиной параболы служит точка (2; -2), а осью параболы — прямая x = 2. Возьмем две пары точек,
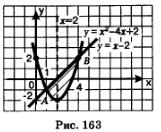
симметричных относительно оси параболы: (1; -1) и (3; -1), (0; 2) и (4; 2) и построим параболу по пяти точкам (рис. 163). Парабола и прямая пересекаются в двух точках A и B, для отыскания абсцисс этих точек надо решить уравнение х2 -4х + 2 = х-2. Находим последовательно:
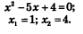
Фигура, площадь которой надо найти, ограничена линиями у = х2 -4x + 2 (снизу) и у = x —2 (сверху). Можно считать, что с боков эта фигура ограничена прямыми x = 1 и x = 4. Значит, для вычисления площади фигуры можно применить формулу (3).
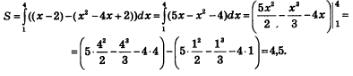
Ответ: S = 4,5.
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|