|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Основные понятия-2(8 класс)
Основные понятия
Определение 1. Квадратным уравнением называют уравнение вида ах2 + их + с = 0, где коэффициенты а, и, с — любые действительные числа, причем
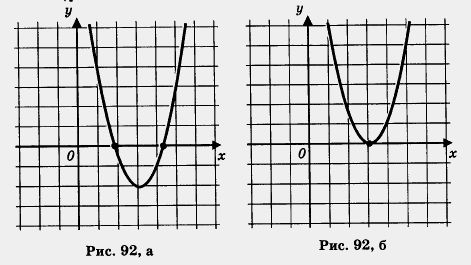
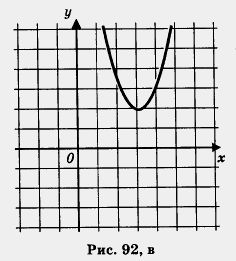
Определение 2. Квадратным уравнением называют приведенным, если его старший коэффициент равен 1; квадратное уравнение называют неприведенным, если старший коэффициент отличен от 1. Определение 3. Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля. Неполное квадратное уравнение — это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b, с равен нулю. Обратите внимание: об ах2 речи нет, этот член всегда присутствует в квадратном уравнении. Определение 4. Корнем квадратного уравнения ах2 + bх + + с — 0 называют всякое значение переменной х, при котором квадратный трехчлен ах2 + bх + с обращается в нуль; такое значение переменной х называют также корнем квадратного трехчлена. Можно сказать и так: корень квадратного уравнения ах2 + + bх + с = 0 — это такое значение х, подстановка которого в уравнение обращает уравнение в верное числовое равенство 0 = 0. Сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать. Рассмотрим несколько таких уравнений. Пример 1. Решить неполные квадратные уравнения: а) 2х2 - 7х = 0; б)-x2 + 5x = 0; в) х2 - 16 = 0; Р е ш е н и е. а) Имеем 2x2 -7x = 0; x( 2x -7) = 0 б) Имеем в) Имеем Ранее, в § 15, мы уже говорили о том, что уравнение вида х2 = а, где а > 0, имеет два корня: г) Имеем -2x2 + 7 = 0; 2x2=7; x2=3,5. Уравнение имеет два корня: д) Имеем Так как выражение Зx2 неотрицательно при любых значениях х, то уравнение Зx2 = - 10 не имеет корней. Иными словами, нет ни одного числа, подстановка которого вместо переменной х обратила бы это уравнение в верное числовое равенство. Иногда в таких случаях уточняют: нет действительных корней. Дело в том, что в математике, кроме действительных чисел, о которых мы впервые упомянули на с. 92, а подробнее поговорим в гл. 5, рассматриваются так называемые мнимые числа; мнимые корни у этого уравнения есть. е) Если 5x2 = 0, то х2 = 0, откуда находим х = 0 — единственный корень уравнения. Этот пример показывает, как решаются неполные квадратные уравнения: 1. Если уравнение имеет вид ах2 = 0, то оно имеет один корень х — 0. 2. Если уравнение имеет вид ах2 + bх = 0, то используется метод разложения на множители: х (ах + b) = 0; значит, либо х = 0, либо ах + b = 0. В итоге получаем два корня: х1 = 0; xl,2=± Мы с вами знаем, что графиком функции у = ах2 + bх + с является парабола. Корнями квадратного уравнения ах2 + bх + с = 0 служат абсциссы точек пересечения параболы у = ах2 + bх + с с осью х. Парабола может пересекать ось х в двух точках, может касаться оси х, т. е. иметь с ней лишь одну общую точку, может вообще не пересекаться с осью х (рис. 92, а, б, в). Это значит, что квадратное уравнение ах2 + bх + с = 0 может иметь либо два корня, либо один корень, либо вообще не иметь корней.
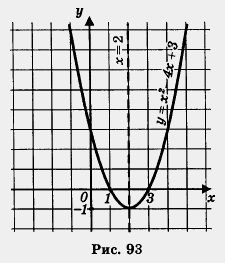
Конечно, неплохо знать, сколько корней имеет квадратное уравнение, но еще лучше уметь находить эти корни. Если уравнение неполное, то, как мы видели выше, особых проблем не возникает. А если мы имеем полное квадратное уравнение? Ниже на примере одного такого уравнения напомним, какими способами мы пользовались до сих пор, когда приходилось встречаться с квадратным уравнением. Пример 2. Решить уравнение х2 - 4х + 3 = 0. Решение. I способ. Рассмотрим квадратный трехчлен х2 — 4х + 3 и разложим его на множители, используя способ группировки; предварительно представим слагаемое - 4х в виде - х - Зх. Имеем Значит, заданное уравнение можно переписать в виде (х - 1) (х - 3) = 0, откуда ясно, что уравнение имеет два корня; х1 = 1, х2 = 3; при х = 1 обращается в нуль множитель х - 1, а при х = 3 обращается в нуль множитель х - 3. II способ. Рассмотрим квадратный трехчлен х2 - 4х + 3 и разложим его на множители, используя метод выделения полного квадрата; предварительно представим слагаемое 3 в виде 4-1. Имеем Воспользовавшись формулой разности квадратов, получим (х - 2 + 1) (х - 2 - 1) = (х - 1) (х - 3). III способ. Построим график функции у = х2 - 4х + 3, воспользовавшись алгоритмом из § 13: 1) Имеем а = 1, b = - 4, х0 = - 2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = 1 и х = 3. Имеем f(1) = f(3) = 0; построим на координатной плоскости точки (1; 0) и (3; 0). 3) Через точки (1; 0), (2; -1), (3;0) проводим параболу (рис. 93).
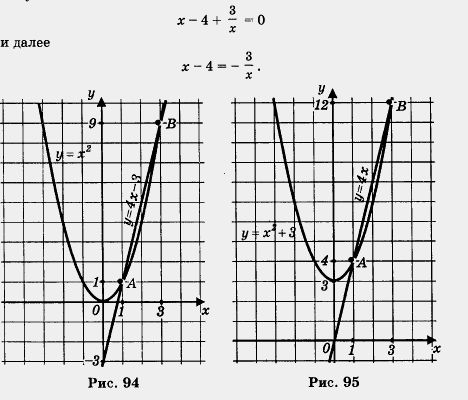
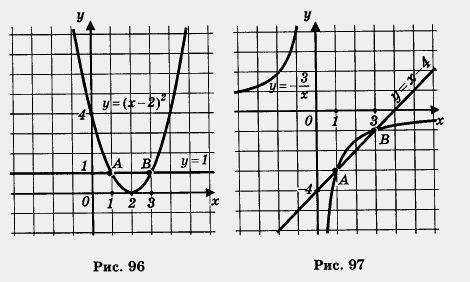
IV способ. Преобразуем уравнение к виду х2 = 4х - 3. Построим в одной системе Рис. 93 координат графики функций у = х2 и у=4х-3 (рис. 94). Они пересекаются в точках А(1; 1) и В(3; 9). Корнями уравнения служат абсциссы точек А и В, поэтому х1 = 1, х2 = 3. V способ. Преобразуем уравнение к виду х2 + 3 = 4х. Построим в одной системе координат графики функций у = х2 + 3 и у = 4х (рис. 95). Они пересекаются в точках А (1; 4) и В (3; 12). Корнями уравнения служат абсциссы точек А и В, таким образом x1 =1; x2 = 3 VI способ. Преобразуем уравнение к виду x2-4x + 4-1 = 0 и далее х2 - 4х + 4 = 1, т. е. (х - 2)2 = 1. Построим в одной системе координат параболу у = (х - 2)2 и прямую у = 1 (рис. 96). Они пересекаются в точках А(1; 1) и В(3; 1). Корнями уравнения служат абсциссы точек А и В, следовательно, х1 = 1, x2 = 3. VII способ. Разделив почленно обе части уравнения на х, получим
Ведь наши успехи в решении квадратных уравнений зависели до сих пор от наличия одного из двух благоприятных обстоятельств: 1) квадратный трехчлен удавалось разложить на множители; 2) графики, которые мы использовали для графического решения уравнения, пересекались в «хороших» точках. Надеяться на такие подарки судьбы математики, естественно, не могли. Они искали универсальный способ, пригодный для решения любых квадратных уравнений, и нашли его; о нем и пойдет речь в следующем параграфе (заметим, что этот способ мы уже упоминали в конце § 15). Планирование по математике , учебники и книги онлайн, курсы и задачи по математике для 8 класса скачать
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: