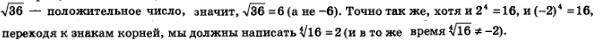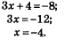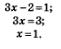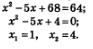|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Понятие корня n-й степени из действительного числа
§ 39. Понятие корня n-й степени из действительного числа
Рассмотрим уравнение x4 =1 и решим его графически. Для этого в одной системе координат построим график функции у = хn прямую у = 1 (рис. 164 а). Они пересекаются в двух точках:
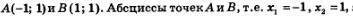 ,являются корнями уравнения х4 = 1. ,являются корнями уравнения х4 = 1.
Рассуждая точно так же, находим корни уравнения х4 =16:
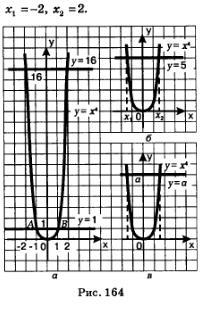
А теперь попробуем решить уравнение х4 =5; геометрическая иллюстрация представлена на рис. 164 б. Ясно, что уравнение имеет два корня x1 и x2, причем эти числа, как и в двух предыдущих случаях, взаимно противоположны. Но для первых двух уравнений корни были найдены без труда (их можно было найти и не пользуясь графиками), а с уравнением х4 =5 имеются проблемы: по чертежу мы не Гложем указать значения корней, а можем только установить, что один корень располагается левее точки -1, а второй — правее точки 1.
Можно доказать (примерно так же, как это сделано в нашем учебнике «Алгебра-8» для числа л/б), что х1 и х2 — иррациональные числа (т.е. бесконечные непериодические десятичные дроби).
Встретившись впервые с подобной ситуацией, математики поняли, что надо придумать способ ее описания на математическом языке. Они ввели в рассмотрение новый символ который назвали корнем четвертой степени, и с помощью этого символа корни уравнения х4 = 5 записали так: 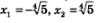 (читается: «корень четвертой степени из пяти»). (читается: «корень четвертой степени из пяти»).
Замечание 1. Сравните эти рассуждения с аналогичными рассуждениями, проведенными в § 17, 32 и 38. Новые термины и новые обозначения в математике появляются тогда, когда они необходимы для описания новой математической модели. Это — отражение особенности математического языка: его основная функция не коммуникативная — для общения, а организующая — для организации успешной работы с математическими моделями в разных областях знаний.
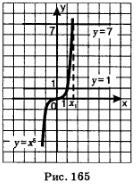
Мы говорили об уравнении х4 =а, где а >0. С равным успехом мы могли говорить и об уравнении х4 =а, гдеа > 0, а п — любое натуральное число. Например, решая графически уравнение х5 = 1, находим х = 1 (рис. 165); решая уравнение х5' = 7, устанавливаем, что уравнение имеет один корень хг, который располагается на оси х чуть правее точки 1 (см. рис. 165). Для числа хх введем обозначение Чч.
Вообще, решая уравнение хп =а, где а >0, n е N, п>1, получаем в случае четного п два корня: 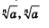 (рис. 164, в); в случае нечетного п — один корень (рис. 164, в); в случае нечетного п — один корень 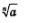 (читается: «корень n-й степени из числа а»). Решая уравнение хп =0, получаем единственный корень х=0. (читается: «корень n-й степени из числа а»). Решая уравнение хп =0, получаем единственный корень х=0.
Замечание 2. В математическом языке, как и в обыденном языке, бывает так, что один и тот же термин применяется к разным понятиям; так, в предыдущем предложении слово « корень» употреблено в двух смыслах: как корень уравнения (к такому толкованию вы давно привыкли) и как корень л-й степени из числа (новое толкование). Обычно из контекста бывает ясно, какое толкование термина имеется в виду.
Теперь мы готовы дать точное определение.
Определение 1. Корнем л-й степени из неотрицательного числа а (n = 2, 3,4, 5,...) называют такое неотрицательное число, которое при возведении в степень n дает в результате число а.
Это число обозначают 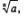 , число а при этом называют подкоренным числом, а число n — показателем корня. , число а при этом называют подкоренным числом, а число n — показателем корня.
Если n=2, то обычно не говорят «корень второй степени», а говорят"«корень квадратный». В этом случае не пишут 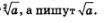 Это тот частный случай, который вы специально изучали в курсе алгебры 8-го класса. Это тот частный случай, который вы специально изучали в курсе алгебры 8-го класса.
Если n = 3, то вместо «корень третьей степени» часто говорят «корень кубический». Первое знакомство с кубическим корнем у вас также состоялось в курсе алгебры 8-го класса. Мы использовали кубический корень в § 36 при решении примера 6.
Итак,
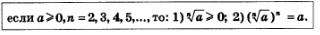
Вообще, 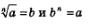 — одна и та же математическая модель (одна и та же зависимость между неотрицательными числами а и Ь), но только вторая описана более простым языком (использует более простые символы), чем первая. — одна и та же математическая модель (одна и та же зависимость между неотрицательными числами а и Ь), но только вторая описана более простым языком (использует более простые символы), чем первая.
Операцию нахождения корня из неотрицательного числа называют обычно извлечением корня. Эта операция является обратной по отношению к возведению в соответствующую степень. Сравните:

Еще раз обратите внимание: в таблице фигурируют только положительные числа, поскольку это оговорено в определении 1. И хотя, например, (-6)6 =36 — верное равенство, перейти от него к записи с использованием квадратного корня, т.е. написать, что 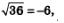 нельзя. По определению нельзя. По определению
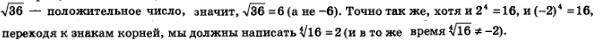
Иногда выражение 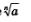 называют радикалом (от латинского слова гаdix — «корень»). В русском языке термин радикальный используется довольно часто, например, «радикальные изменения» — это значит «коренные изменения». Между прочим, и само обозначение корня напоминает о слове гаdix: символ — это стилизованная буква r. называют радикалом (от латинского слова гаdix — «корень»). В русском языке термин радикальный используется довольно часто, например, «радикальные изменения» — это значит «коренные изменения». Между прочим, и само обозначение корня напоминает о слове гаdix: символ — это стилизованная буква r.
Пример 1. Вычислить:

г) В отличие от предыдущих примеров мы не можем указать точное значение числа 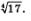 Ясно лишь, что оно больше, чем 2, но меньше, чем 3, поскольку 24=16 (это меньше, чем 17), а З4 = 81 (это больше, чем 17). Замечаем, что 24 намного ближе к 17, чем З4, так что есть основания использовать знак приближенного равенства: Ясно лишь, что оно больше, чем 2, но меньше, чем 3, поскольку 24=16 (это меньше, чем 17), а З4 = 81 (это больше, чем 17). Замечаем, что 24 намного ближе к 17, чем З4, так что есть основания использовать знак приближенного равенства: 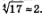
Впрочем, более точное приближенное значение числа 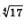 можно найти с помощью калькулятора, который содержит операцию извлечения корня, оно равно приближенно можно найти с помощью калькулятора, который содержит операцию извлечения корня, оно равно приближенно 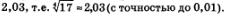
Операцию извлечения корня определяют и для отрицательного подкоренного числа, но только в случае нечетного показателя корня. Иными словами, равенство (-2)5 =-32 можно переписать в эквивалентной форме как 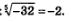 . При этом используется следующее определение. . При этом используется следующее определение.
Определение 2. Корнем нечетной степени л из отрицательного числа а (n = 3,5,...) называют такое отрицательное число, которое, будучи возведено в степень n, дает в результате число а.
Это число, как и в определении 1, обозначают 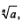 , число а — подкоренное число, число n — показатель корня. , число а — подкоренное число, число n — показатель корня.
Итак,

Таким образом, корень четной степени имеет смысл (т.е. определен ) только для неотрицательного подкоренного выражения; корень нечетной степени имеет смысл для любого подкоренного выражения.
Пример 2. Решить уравнения:
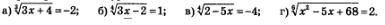
Решение: а) Если 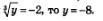 Фактически обе части заданного уравнения мы должны возвести в куб. Получим: Фактически обе части заданного уравнения мы должны возвести в куб. Получим:
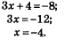
б) Рассуждая, как в примере а), возведем обе части уравнения в четвертую степень. Получим:
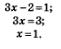
в) Здесь не надо возводить в четвертую степень, это уравнение не имеет решений. Почему? Потому, что согласно определению 1 корень четной степени — неотрицательное число.
г) Возведя обе части уравнения в шестую степень, получим:
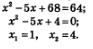
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|