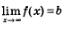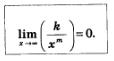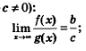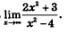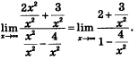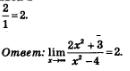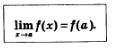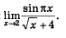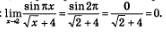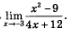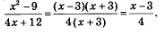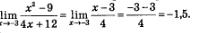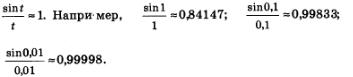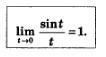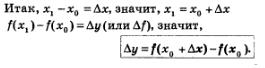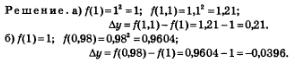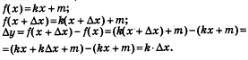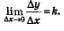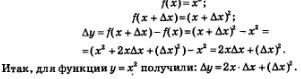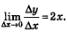|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Предел функции
§ 31. Предел функции
1. Предел функции на бесконечности
В § 30 мы получили следующий результат: равенство 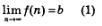 означает, что прямая у = b является горизонтальной асимптотой графика функции у = f (n) (рис. 105). Напомним, что аргумент п принимает только натуральные значения. означает, что прямая у = b является горизонтальной асимптотой графика функции у = f (n) (рис. 105). Напомним, что аргумент п принимает только натуральные значения.
Пусть теперь дана функция у =f(n), в области определения которой содержится луч 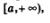 и пусть прямая у = Ь является горизонтальной асимптотой графика (рис. 106) функции у =f(x). Естественно, что математики в этом случае по аналогии с приведенным выше равенством (1) решили использовать запись: и пусть прямая у = Ь является горизонтальной асимптотой графика (рис. 106) функции у =f(x). Естественно, что математики в этом случае по аналогии с приведенным выше равенством (1) решили использовать запись:
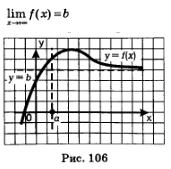
(читают: предел функции у = f(х) при стремлении х к плюс бесконечности равен b).
Если же дана функция у = f (х), в области определения которой содержится луч a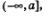 и прямая у = Ь является горизонтальной асимптотой графика функции у = f(х) (рис. 107), то в этом случае используют запись: и прямая у = Ь является горизонтальной асимптотой графика функции у = f(х) (рис. 107), то в этом случае используют запись:
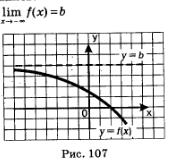
(читают: предел функции у =f(х) при стремлении х к минус бесконечности равен b).
Если одновременно выполняются два соотношения:
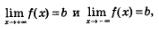
то можно объединить их одним соотношением: 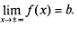 Но условились использовать более экономную запись: Но условились использовать более экономную запись:
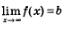
(читают: предел функции у = f(х) при стремлении х к бесконечности равен Ь).
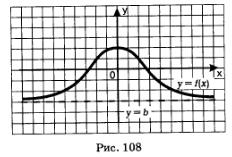
В этом случае прямая у = Ь является горизонтальной асимптотой графика функции у = f(х) как бы с двух сторон (рис. 108).
Вычисление предела функции на бесконечности осуществляется по тем же правилам, что и вычисление предела последовательности. Приведем их (с соответствующими изменениями).
1) Для любого натурального показателя m и любого коэффициента к справедливо соотношение:
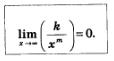
2) Если 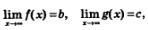 , то , то
а) предел суммы равен сумме пределов:
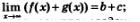
б) предел произведения равен произведению пределов:
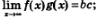
в) Предел частного равен частному от деления пределов (разумеется, при условии, что 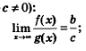
г) постоянный множитель можно вынести за знак предела:
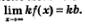
Пример 1. Вычислить 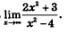
Решение. Разделим числитель и знаменатель дроби почленно на х2:
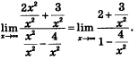
Осталось воспользоваться правилом «предел частного». Поскольку предел числителя равен 2 + 0 = 2, а предел знаменателя равен 1 -0 = 1, то 2
предел дроби равен
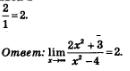
Замечание. Сравните только что решенный пример с примером 6 из § 30: все то же самое — та же идея, те же рассуждения. Отличие только одно: там переменная п принимала лишь натуральные значения, а здесь переменная х принимает любые действительные значения (кроме, разумеется, значений -2 и 2, которые обращают в нуль знаменатель дроби, содержащейся под знаком предела).
2. Предел функции в точке
Рассмотрим функции, графики которых изображены на рис. 109—111. Во всех трех случаях изображена одна и та же кривая, тем не менее это три разные функции, они отличаются друг
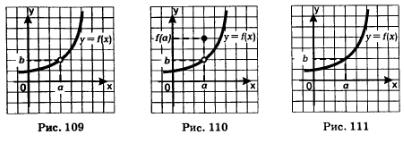
от друга своим поведением в точке х =а. Для функции у = f(х), график которой изображен на рис. 109, значение f(а) не существует, функция в указанной точке не определена. Для функции у = f (х), график которой изображен на рис. 110, значение f (а) существует, но оно «неудачное», оно отлично, от, казалось бы, естественного значения Ъ. Наконец, для функции у = f(х), график которой изображен на рис. 111, значение f(а) существует, и оно «удачное». Если же точку х=а исключить из рассмотрения, то все три функции будут тождественными.
Для всех трех случаев используется одна и та же запись:
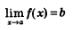
(читаем: «предел функции у =f( х ) при стремлении х к а равен b» ).
Содержательный смысл приведенной выше записи заключается в следующем: если значения аргумента выбираются все ближе и ближе к значению х =а, то значения функции все меньше и меньше отличаются от предельного значения Ъ. Можно сказать и так: в достаточно малой окрестности точки а справедливо приближенное равенство:
f(x)=b (причем это приближенное равенство тем точнее, чем меньшая окрестность выбирается). При этом, подчеркнем еще раз, сама точка х =а исключается из рассмотрения.
А теперь ответьте на вопрос: какую из рассмотренных трех функций естественно считать непрерывной в точке х=а? Ответ очевиден: непрерывной естественно считать третью функцию, которая удовлетворяет условию 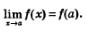
В каких случаях мы с вами до сих пор использовали понятие «непрерывная функция» ? Мы говорили, что функция непрерывна, если видели, что ее график представляет собой сплошную линию, т.е. не имеет «проколов» и «скачков». На самом деле график функции изображают в виде сплошной линии (без «проколов» и «скачков») только тогда, когда установлена непрерывность функции. При этом функцию у = f(х) называют непрерывной в точке х = а, если выполняется соотношение:
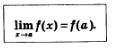
Иными словами, функцию у = f(х) называют непрерывной в точке х=а, если предел функции у = f(х) при стремлении х к а равен значению функции в точке х=а.
Функцию у = f(х) называют непрерывной на промежутке X, если она непрерывна в каждой точке промежутка.
В курсе алгебры 7—9-го классов мы отмечали, что функции: 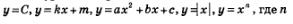 — натуральное число, — непрерывны на всей числовой прямой. Отмечали также, что функция — натуральное число, — непрерывны на всей числовой прямой. Отмечали также, что функция 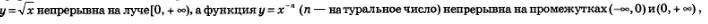 но претерпевает разрыв в точке х =0. В главе 1, говоря о тригонометрических функциях, мы отмечали непрерывность функций у = sin х и у=соs х на всей числовой прямой, а также непрерывность функций у = х, у=х в каждом промежутке из области их определения. До сих пор мы опирались на наглядные представления и интуицию. Математики доказали, опираясь на определение непрерывности, что все упомянутые утверждения верны. Так что теперь мы будем ими пользоваться на законных основаниях. но претерпевает разрыв в точке х =0. В главе 1, говоря о тригонометрических функциях, мы отмечали непрерывность функций у = sin х и у=соs х на всей числовой прямой, а также непрерывность функций у = х, у=х в каждом промежутке из области их определения. До сих пор мы опирались на наглядные представления и интуицию. Математики доказали, опираясь на определение непрерывности, что все упомянутые утверждения верны. Так что теперь мы будем ими пользоваться на законных основаниях.
Между прочим, математики доказали более сильное утверждение:
Если выражение f(х) составлено из рациональных, иррациональных, тригонометрических выражений, то функция у = f(х) непрерывна в любой точке, в которой определено выражение f (х).
Рассмотрим несколько примеров на вычисление пределов функций.
Пример 2. Вычислить: 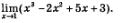
Решение. Выражение 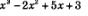 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция определено в любой точке х, в частности, в точке х = 1. Следовательно, функция 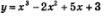 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1. непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.
Имеем: 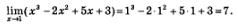
Ответ: 7.
Пример 3. Вычислить: 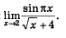
Решение. Выражение  , в частности, в точке х = 2. Следовательно, функция у = f(х)непрерывна в точке х = 2, а потому предел функции при стремлении х к 2 равен значению , в частности, в точке х = 2. Следовательно, функция у = f(х)непрерывна в точке х = 2, а потому предел функции при стремлении х к 2 равен значению
функции в точке х = 2. Имеем:
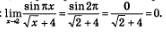
Ответ: 0.
Вы заметили, наверное, что в рассмотренных примерах вычисление пределов не составило значительных сложностей: достаточно было найти значение функции в точке, к которой стремится аргумент х. Но часты случаи, когда этот прием не срабатывает.
Пример 4. Вычислить
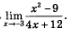
Решение. Если подставить значение х = -3 в заданное выражение, то и в числителе, и в знаменателе получится 0, а на 0 делить нельзя. Но заданную алгебраическую дробь можно сократить:
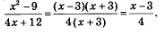
Значит, функции

Но (внимание!) при вычислении предела функции при х —» -3 саму точку х = -3 можно исключить из рассмотрения, мы об этом говорили выше. Значит,
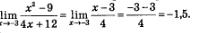
Ответ: -1,5.
Вернемся снова к названию раздела математики, который мы начали изучать, — математический анализ. В начале главы 4 мы отметили: анализируют в этом разделе математики то, как ведет себя функция около, конкретной точки. Теперь мы можем сказать точнее: в окрестности конкретной точки. Именно этим мы и занимались, делая выводы о функциях, графики которых изображены на рис. 109—111. Проведенный краткий анализ привел нас к понятию предела функции в точке и к понятию непрерывности функции в точке.
Важное замечание. Теория пределов — достаточно сложный раздел математического анализа, который изучается в вузах. Наше знакомство с понятием предела, как вы, наверное, заметили, поверхностное, основанное на интуиции и наглядных представлениях. Продолжая это «шапочное» знакомство, получим один очень существенный для высшей математики результат. При этом опять будем использовать не строгие рассуждения (нам пока это не по силам), а рассуждения, основанные на интуиции, наглядности, правдоподобии. Такие рассуждения математики часто называют рассуждениями «на пальцах».
Возьмем числовую окружность, выберем достаточно малое положительное значение t, отметим на окружности точку М(?) и ее ординату, т.е. sin t — это длина дуги АМ, sin t — это длина
перпендикуляра МР (рис. 112). Для достаточно малых значений t выполняется приближенное равенство АМ-МР, т.е. sin t=t, и, следовательно,
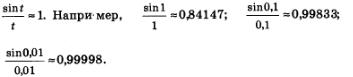
Естественно предположить, что
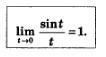
В курсе математического анализа доказано, что это утверждение верно.
3. Приращение аргумента. Приращение функции
Изучая поведение функции у = f(х) около конкретной точки х0, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используются понятия приращений аргумента и функции.
Определение 1. Пусть функция у =f(х) определена в точках х0 и х1 Разность х, -х0 называют приращением аргумента (при переходе от точки х0 кх,), а разность f(х,)-f(х0) называют приращением функции.
Приращение аргумента обозначают 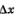 (читают: «дельта икс»; А — прописная буква греческого алфавита «дельта», а соответствующая строчная буква пишется так: (читают: «дельта икс»; А — прописная буква греческого алфавита «дельта», а соответствующая строчная буква пишется так: 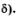 Приращение функции обозначают Приращение функции обозначают 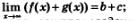
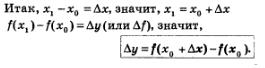
Пример 5. Найти приращение функции у = х1 при переходе от точки х0 =1 к точкам: а) х = 1,1; б) х = 0,98. 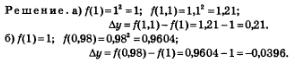
Обратите внимание на полученный в примере 5 ответ: приращение функции (как, впрочем, и приращение аргумента) может быть и положительным, и отрицательным числом, так что не истолковывайте термин «приращение» как «прирост».
А теперь посмотрим на определение непрерывной функции с точки зрения приращений аргумента и функции. Определение непрерывности функции в точке х =а выглядит так:
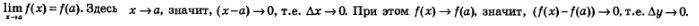
Получаем новое истолкование понятия непрерывности функции в точке.
Функция у = f(х) непрерывна в точке х =а, если в точке х =а выполняется следующее условие:
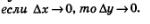
Пример 6. Для функции у = кх + m найти:
а) приращение функции при переходе от фиксированной точки х к точке х + f(х;
б) предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение, а)Имеем:
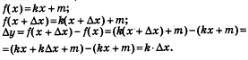
Итак, для заданной линейной функции у =кх + m. получили: 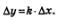
б) Нужно вычислить
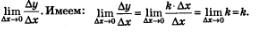
Итак, для заданной линейной функции у=кх + m получили:
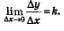
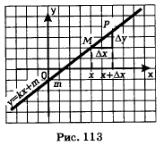
На рис. 113 изображен график линейной функции у = kх+m, выделена фиксированная точка графика М(х, f(х)), отмечены приращения аргумента и функции при переходе от точки х к точке 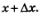 Чер- Чер-
теж подсказывает, что 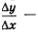 тангенс угла между прямой у = кх + m и положительным направлением оси х, а это — угловой коэффициент прямой. Значит, тангенс угла между прямой у = кх + m и положительным направлением оси х, а это — угловой коэффициент прямой. Значит, 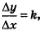 что фактически и получено при что фактически и получено при
решении примера 6, но с помощью формальных преобразований.
Пример 7. Для функции у = х2 найти:
а) приращение функции при переходе от фиксированной точки х к точке 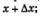
б) предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение. а) Имеем:
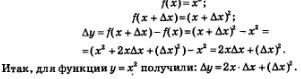
б) Нужно вычислить 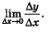
Имеем: 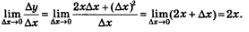
При вычислении последнего предела мы учли, что х — фиксированная точка, т.е. постоянное число, а 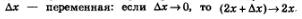
Итак, для заданной функции у = х2 получили: 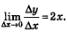
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|