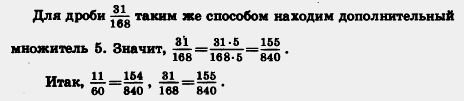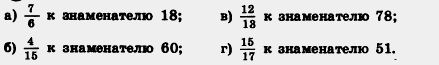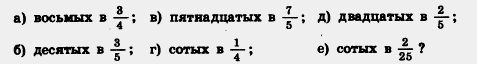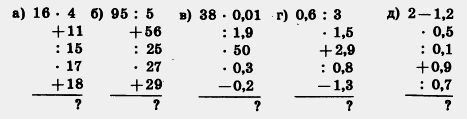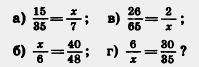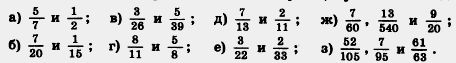|
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Приведение дробей к общему знаменателю
10. Приведение дробей к общему знаменателю
Умножим числитель и знаменатель дроби 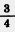 на одно и то же число 2. Получим равную ей дробь , т. е. на одно и то же число 2. Получим равную ей дробь , т. е.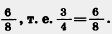 Говорят, что мы правели дробь Говорят, что мы правели дробь 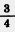 к новому знаменателю 8. Дробь можно привести к любому знаменателю , кратному знаменателю данной дроби. к новому знаменателю 8. Дробь можно привести к любому знаменателю , кратному знаменателю данной дроби.
Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем.
При приведении дроби к новому знаменателю ее числитель и знаменатель умножают на дополнительный множитель.
Пример 1. Приведем дробь 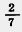 к знаменателю 35. к знаменателю 35.
Решение. Число 35 кратно 7, так как 35:7 = 5. Дополнительным множителем является число 5. Умножим числитель и знаменатель данной десятичные дроби на 5, получим 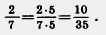
Любые две дроби можно привести к одному и тому же знаменателю, или иначе к общему знаменателю.
Например, 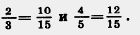
Общим знаменателем дробей может быть любое общее кратное их знаменателей (например, произведение знаменателей).
Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Пример 2. Приведем к наименьшему общему знаменателю дроби 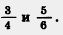
Решение. Наименьшим общим кратным чисел 4 и 6 является 12.
Чтобы привести дробь 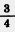 к знаменателю 12, надо умножить числитель и знаменатель этой дроби на дополнительный к знаменателю 12, надо умножить числитель и знаменатель этой дроби на дополнительный
множитель 3 (12:4 = 3). Получим 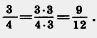
Чтобы привести дробь 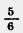 к знаменателю 12, надо числитель и знаменатель этой дроби умножить на дополнительный множитель 2 (12:6=2). к знаменателю 12, надо числитель и знаменатель этой дроби умножить на дополнительный множитель 2 (12:6=2).
Получим 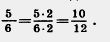
Итак 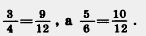 а а
Чтобы привести дроби к наименьшему общему знаменателю, надо:
1) найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель;
3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
В более сложных случаях наименьший общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Пример 3. Приведем дроби 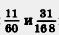 к наименьшему общему знаменателю. к наименьшему общему знаменателю.
Решение. Разложим знаменатели данных дробей на простые множители: 60=2 • 2 • 3 • 5; 168 = 2 • 2 • 2 • 3 • 7. Найдем наименьший общий знаменатель:
2 • 2 • 2 • 3 • 5 • 7 = 840.
Дополнительным множителем для дроби 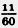 является произведение 2 • 7, т. е. тех множителей, которые надо добавить к разложению числа 60, чтобы получить разложение общего знаменателя 840. Поэтому является произведение 2 • 7, т. е. тех множителей, которые надо добавить к разложению числа 60, чтобы получить разложение общего знаменателя 840. Поэтому 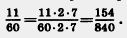
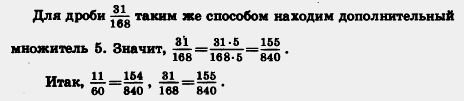
? К какому новому знаменателю можно привести данную дробь? Можно ли привести дробь к знаменателю 35? к знаменателю 25? Какое число называют дополнительным множителем? Как найти дополнительный множитель? Какое число может служить общим знаменателем двух дробей? Как привести дроби к наименьшему общему знаменателю?
К 264. Приведите дробь:
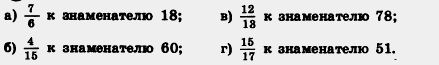
265. Выразите в минутах, а потом в шестидесятых долях часа:
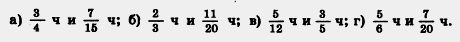
266. Сколько содержится:
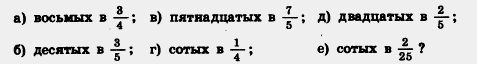
267. Сократите дроби 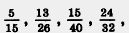 а потом приведите их к знаменателю 24. а потом приведите их к знаменателю 24.
268. Можно ли привести к знаменателю 36 дроби:
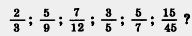
269. Можно ли представить в виде десятичной дроби:
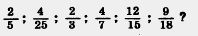
270. Запишите в виде десятичной дроби, приведя:

271. Запишите в виде десятичной дроби:
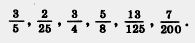
272. Приведите к наименьшему общему знаменателю дроби:

273. Вычислите усно:
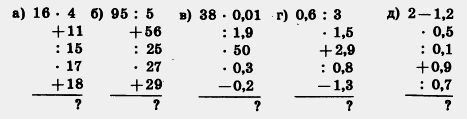
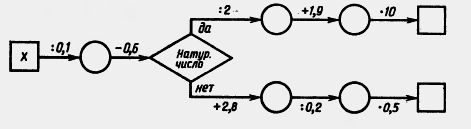
274. Найдите пропущенные числа, если х=0,8; 0,16; 0,06; 1:
275. На какое число надо умножить 24; 8; 16; 6; 12, чтобы получить 48?
276. С помощью транспортира разделите одну окружность на 6, а другую на 3 равные дуги. Постройте многоугольники, изображенные на рисунке 14. У каждого из этик многоугольников равны стороны и равны углы. Такие многоугольники называют правельными. Подумайте, является ли правильным многоугольником прямоугольник; квадрат.

277 Сократите:
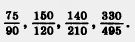
278. Найдите наибольший общий делитель числителя и знаменателя и сократите дробь:
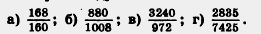
279. При каком значении х верно равенство:
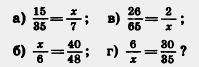
280. Жук ползет вверх по стволу дерева (рис. 15) со скоростью 6 см/с. По тому же дереву ползет вниз гусеница. Сейчас она находится на 60 см ниже жука. С какой скоростью ползет гусеница, если через 5 с расстояние между ней и жуком будет 100 см?
281. Космический корабль «Вега-1» двигался к комете Галлея со скоростью 34 км/с, а сама комета двигалась ему навстречу со скоростью 46 км/с. Какое расстояние было между ними за 15 мин до встречи? "
282. Сократите: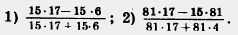
283. Найдите значение выражения:

284 Выполните действия и проверьте ваши вычисления с помощью микрокалькулятора:
1) 111 - ((0,9744:0,24 +1,02) • 2,5 - 2,7 5);
2) 200 - ((9,08 - 2,6828:0,38) • 8,5 + 0,84).
Д 285. Приведите дробь:

286. Представьте в виде десятичной дроби:
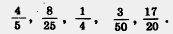
287. Сократите дроби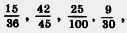 а потом приведите их к знаменателю 60. а потом приведите их к знаменателю 60.
288. Приведите дроби к наименьшему общему знаменателю:
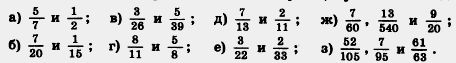
289. Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу одновременно отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если известно, что они встретились через 2,5 ч после своего выхода.
290. Из двух пунктов, расстояние между которыми 210 км, вышли одновременно навстречу друг другу два электропоезда. Скорость одного из них на 5 км/ч больше скорости другого. Найдите скорость каждого электропоезда, если они встретились через 2 ч после своего выхода.
291. Выполните действия:
а) 62,3+(50,1 - 3,3 • (96,96:9,6)) 1,8;
б) 51,6 + (70,2 - 4,4 • (73,73:7,3)) • 1,6.
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Сборник конспектов уроков по математике скачать, календарно-тематическое планирование, учебники по всем предметам онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|