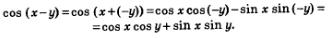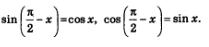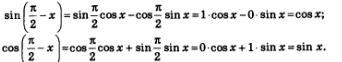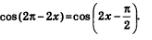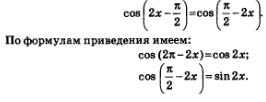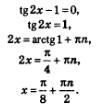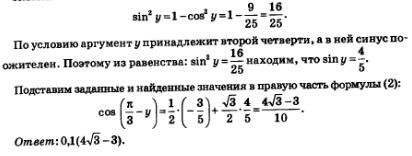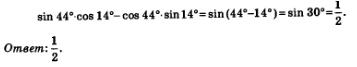|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Синус и косинус разности аргументов
§ 22. Синус и косинус разности аргументов
Рассмотрим выражение sin (х-у). Если переписать его в виде sin (x+(-у)), то появляется возможность применить формулу синуса суммы для аргументов х и-у:
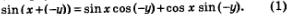
А теперь воспользуемся тем, что
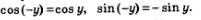
Это позволяет правую часть равенства (1) переписать в виде 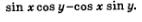
Таким образом, мы вывели следующую формулу, называемую на практике синус разности:

Аналогичные рассуждения позволяют вывести формулу косинуса разности (мы сделаем это «молча», а вы «озвучьте» написанное):
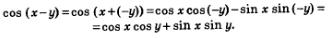
Итак, перед вами формула косинуса разности:
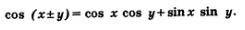
Естественно, что формулы синуса разности и косинуса разности применяются на практике в написании как слева направо, так и справа налево.
Пример 1. Вычислить sin 15° и соs 15°.
Решение. Воспользуемся тем, что 15о = 45°-30°,и тем, что значения синуса и косинуса углов 45° и 30° мы знаем:

Пример 2. Доказать, что 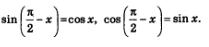
Решение. Имеем:
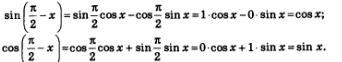
Замечание. В § 21 мы вывели две формулы приведения с помощью формул синуса и косинуса суммы аргументов. В только что решенном примере 2 мы вывели еще две формулы приведения с помощью формул синуса и косинуса разности аргументов. Вообще все формулы приведения для синуса и косинуса, о которых мы говорили в § 8, без труда выводятся с помощью формул синуса и косинуса суммы или разности аргументов.
Пример 3. Решить уравнение 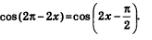
Решение. Мы знаем, что соs (-t)=соs t значит, 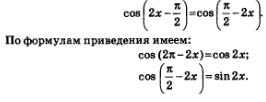
Это позволяет переписать заданное уравнение в более простом виде: 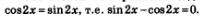
Мы получили однородное уравнение первой степени, о решении которого шла речь в § 20, более того, там же в примере 2 было решено уравнение, очень похожее на полученное. Разделив обе части уравнения почленно на соs 2x:, получим:
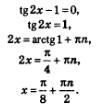
Пример 4. Вычислить 
Решение. Воспользуемся формулой косинуса разности:
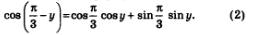
Значение соs у задано в условии, значения 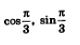 известны, они равны соответственно известны, они равны соответственно 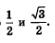 Осталось вычислить значение sin у. Осталось вычислить значение sin у.
Имеем:
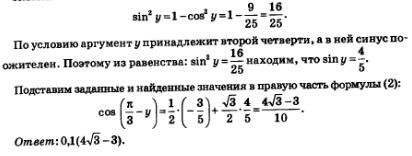
Пример 5. Решить уравнение:

Пример 6. Вычислить sin44°соs14°-sin 46° соs 76°.
Решение. По формулам приведения находим:
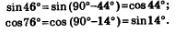
Это значит, что мы имеем право в заданном выражении заменить sin 46° на соs 44°, а соs 76°на sin 14°. Тогда заданное выражение можно переписать ввиде: sin 44° соs 14°-соs 44°-sin 14°и «свернуть» его в синус разности аргументов 44° и 14°. Получим:
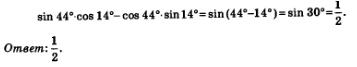
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|