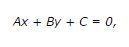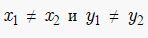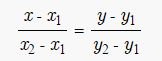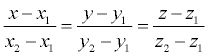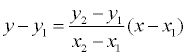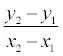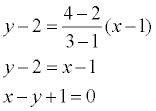|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Уравнение прямой
Свойства прямойВы уже изучали тему о прямой и знаете, что через какую-либо точку можно проводить бесконечное множество прямых. Но если точки не совпадают, то через них можно проводить только одну прямую. Если же мы имеем две несовпадающие прямые, которые лежат на плоскости, то из предыдущего определения следует, что они либо пересекаются в одной точке, либо же являются параллельными. Если же рассматривать расположение 2-х прямых в трехмерном пространстве, то здесь существует три варианта: • Первый, когда прямые пересекаются; Также стоит вспомнить, что прямая линия в декартовой системе координат, как правило, задается на плоскости уравнением 1-степени, то есть линейным уравнением. Общее уравнение прямой на плоскостиА теперь пришло время познакомиться с общим уравнением прямой, так как в геометрии нам придется иметь дело именно с ним. Поэтому следует знать следующее определение, в котором говориться, что любая прямая, которая есть на плоскости может быть задана уравнением первого порядка. Это общее уравнение прямой представлено нам в таком виде:
Но здесь следует запомнить, что такие постоянные коэффициенты А и В единовременно не могут равняться нулю, поскольку такое уравнение потеряет всякий смысл. Теперь мы с вами выяснили, что приведенное выше уравнение первого порядка, как раз и является общим уравнением прямой. А вот в зависимости от значений постоянных А, В и С мы с вами рассмотрим возможные частные варианты: Уравнение прямой, проходящей через две точкиПрипустим у нас имеются 2 точки А(x1, y1) и В (x2, y2) и через них проходит прямая. Но следует отметить, что точки: То в таком случае уравнение можно найти, если использовать следующую формулу: Уравнение прямой в пространствеТеперь давайте представим, что нам дана прямая, проходящая через точки А(х1, у1, z1) и В (х2, у2, z2), тогда, в этом случае уравнение прямой, проходящей через эти точки будет иметь такой вид: Здесь стоит акцентировать внимание на то, что когда какой-то из этих знаменателей будет равен нулю, то необходимо и соответствующий числитель также приравнять к нулю. Теперь давайте запишем это уравнение в упрощенном виде и смотрим, какой вид оно приобрело: В случае, если x1≠x2 и x = x1, если x1=x2. Даная дробь, которая имеет вид: будет равна = k и является угловым коэффициентом прямой. Пример. Теперь давайте более подробно рассмотрим на конкретном примере. Припустим, нам нужно найти уравнение прямой, проходящей через такие точки А(1,2) и В (3,4). Решение. Если мы с вами к этим данным применим формулу, которую мы рассматривали выше, то у нас получится такой результат: Решение задачНам даны точки А (-1, 1) и В (1, 0). Нужно составить уравнение прямой, проходящей через данные точки. Решение. Нам уже известно, что для данной прямой имеет место уравнение такого вида, как ax + by + c = 0. А так как нам известно, что точки А и В лежат на прямой, то отсюда следует вывод, что координаты этих точек соответствуют для решения этого уравнения. Поэтому мы берем и подставляем в это уравнение координаты данных точек и в итоге получаем: -a+ b+ c = 0, a + c = 0. Следуя результатам уравнения, появляется возможность выразить два коэффициента через третий. Например, а и b через а = -c, а b = -2c. Теперь возьмем и подставим эти значения а и b в уравнение прямой. Смотрим, что у нас получилось: - cx– 2cy + c = 0 Мы видим, что данное уравнение можно сократить, и в результате получаем уравнение нашей прямой, которое будет выглядеть так: -x – 2y + 1 = 0 |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: