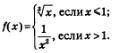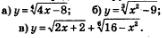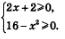|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Функции вида y = √x, их свойства и графики
§40. Функции вида y = √x, их свойства и графики
В предыдущем параграфе мы ввели понятие корня n-й степени из действительного числа, отметили, что из любого неотрицательного числа можно извлечь корень любой степени (второй, третьей, четвертой и т.д.), а из отрицательного числа можно извлечь корень любой нечетной степени. Но тогда следует подумать и о функции вида 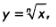 , о ее графике, о ее свойствах. Этим мы и займемся в нас стоящем параграфе. Сначала поговорим о функции , о ее графике, о ее свойствах. Этим мы и займемся в нас стоящем параграфе. Сначала поговорим о функции 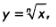 в случае неотрицательных значений аргумента. в случае неотрицательных значений аргумента.
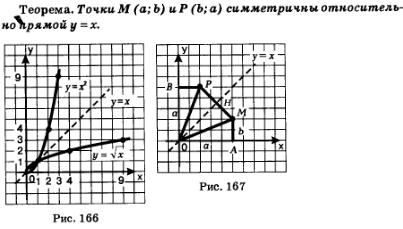
Начнем с известного вам случая, когда n =2, т.е. с функции На рис. 166 изображен график функции 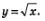 и график функции у = х2, х>0. Оба графика представляют собой одну и ту же кривую — ветвь параболы, только по-разному расположенную на координатной плоскости. Уточним: эти графики симметричны относительно прямой у = х, поскольку состоят из точек, симметричных друг другу относительно указанной прямой. Смотрите: на рассматриваемой ветви параболы у = х2 есть точки (0; 0), (1; 1), (2; 4), (3; 9), (4; 16), и график функции у = х2, х>0. Оба графика представляют собой одну и ту же кривую — ветвь параболы, только по-разному расположенную на координатной плоскости. Уточним: эти графики симметричны относительно прямой у = х, поскольку состоят из точек, симметричных друг другу относительно указанной прямой. Смотрите: на рассматриваемой ветви параболы у = х2 есть точки (0; 0), (1; 1), (2; 4), (3; 9), (4; 16), 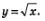 а на графике функции точки (0; 0), (1; 1), (4; 2), (9; 3), (16; 4). а на графике функции точки (0; 0), (1; 1), (4; 2), (9; 3), (16; 4).
Точки (2; 4) и (4; 2), (3; 9) и (9; 3), (4; 16) и (16; 4) симметричны относительно прямой у = х, (а точки (0; 0) и (1; 1) лежат на этой прямой). И вообще, для любой точки (а; а2) на графике функции у = х2 есть симметричная ей относительно прямой у = x точка (а2; а) на графике функции 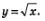 и обратно. Справедлива следующая теорема. и обратно. Справедлива следующая теорема.
Доказательство. Будем считать для определенности, что а и b — положительные числа. Рассмотрим треугольники ОАМ и ОВР (рис. 167). Они равны, значит, ОР = ОМ и 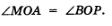 . Но тогда и . Но тогда и 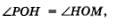 поскольку прямая у = х — биссектриса угла АОВ. Итак, треугольник РОМ — равнобедренный, ОН — его биссектриса, а значит, и ось симметрии. Точки М и Р симметричны относительно прямой ОН, что и требовалось доказать. поскольку прямая у = х — биссектриса угла АОВ. Итак, треугольник РОМ — равнобедренный, ОН — его биссектриса, а значит, и ось симметрии. Точки М и Р симметричны относительно прямой ОН, что и требовалось доказать.
Итак, график функции 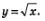 можно получить из графика функции у = х2, х>0 с помощью преобразования симметрии относительно прямой у = х. Аналогично график функции можно получить из графика функции у = х2, х>0 с помощью преобразования симметрии относительно прямой у = х. Аналогично график функции 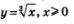 можно получить из графика функции у = х3, х> 0 с помощью преобразования симметрии относительно прямой у=х; график функции можно получить из графика функции у = х3, х> 0 с помощью преобразования симметрии относительно прямой у=х; график функции 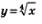 можно получить из графика функции можно получить из графика функции 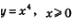 с помощью преобразования симметрии относительно прямой у = х и т.д. Напомним, что график функции с помощью преобразования симметрии относительно прямой у = х и т.д. Напомним, что график функции 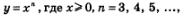 напоминает по виду ветвь параболы напоминает по виду ветвь параболы 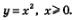 Чем больше п, тем круче эта ветвь устремляется вверх на промежутке Чем больше п, тем круче эта ветвь устремляется вверх на промежутке 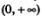 и тем ближе подходит к оси х в окрестности точки х=0 (рис. 168). и тем ближе подходит к оси х в окрестности точки х=0 (рис. 168).
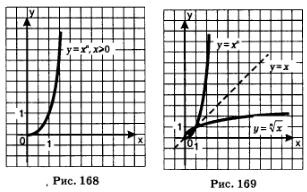
Сформулируем общий вывод: график функции 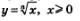 симметричен графику функции симметричен графику функции 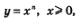 , относительно прямой у = х(рис. 169). , относительно прямой у = х(рис. 169).
Свойства функции 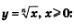
1) 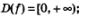
2) функция не является ни четной, ни нечетной;
3) возрастает на 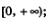
4) не ограничена сверху, ограничена снизу;
5) не имеет наибольшего значения; 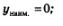
6) непрерывна;
7) 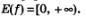
Обратите внимание на одно любопытное обстоятельство. Рассмотрим две функции, графики которых изображены на рис. 169: 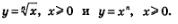 Только что мы перечислили семь свойств для первой функции, но абсолютно теми же свойствами обладает и вторая функция. Словесные «портреты» двух различных функций одинаковы. Но, уточним, пока одинаковы. Только что мы перечислили семь свойств для первой функции, но абсолютно теми же свойствами обладает и вторая функция. Словесные «портреты» двух различных функций одинаковы. Но, уточним, пока одинаковы.
Математики не смогли вынести такой несправедливости, когда разные функции, имеющие разные графики, словесно описываются одинаково, и ввели понятия выпуклости вверх и выпуклости вниз. График функции 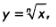 обращен выпуклостью вверх, тогда как график функции у = хп обращен выпуклостью вниз. обращен выпуклостью вверх, тогда как график функции у = хп обращен выпуклостью вниз.
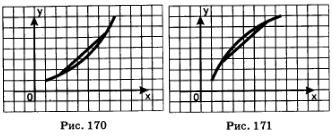
Обычно говорят, что непрерывная функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка (рис. 170); непрерывная функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка (рис. 171).
Свойство выпуклости мы будем в дальнейшем включать в процедуру чтения графика. Отметим его'(продолжив нумерацию описанных ранее свойств) для рассматриваемой функции:
8) функция 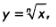 выпукла вверх на луче выпукла вверх на луче 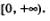
В предыдущей главе мы познакомились еще с одним свойством функции — дифференцируемостью, видели, что функция у = хп дифференцируема в любой точке, ее производная равна пхn-1. Геометрически это означает, что в любой точке графика функции у = хп к нему можно провести касательную. Этим же свойством обладает и график функции 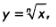 : в любой его точке к графику можно провести касательную. Таким образом, мы можем отметить еще одно свойство функции : в любой его точке к графику можно провести касательную. Таким образом, мы можем отметить еще одно свойство функции 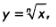
9) функция 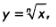 дифференцируема в любой точке х > 0. дифференцируема в любой точке х > 0.
Обратите внимание: о дифференцируемости функции в точке х = 0 речь не идет — в этой точке касательная к графику функции совпадает с осью у, т.е. перпендикулярна оси абсцисс.
Пример 1. Построить график функции 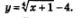
Решение.1)Перейдем к вспомогательной системе координат с началом в точке (-1; -4) — пунктирные прямые х = -1 и у = -4 на рис. 172.
2) «Привяжем» функцию 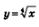 к новой системе координат. Это и будет требуемый график. к новой системе координат. Это и будет требуемый график.
Пример 2. Решить уравнение 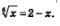
Решение. Первый способ. 1) Введем в рассмотрение две функции 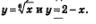
2) Построим график функции
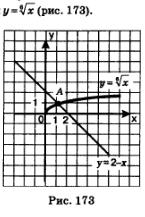
3) Построим график линейной функции у=2-х (см. рис. 173).
4) Построенные графики пересекаются в одной точке А, причем по графику можно сделать предположение, что координаты точкиА таковы: (1; 1). Проверка показывает, что на самом деле точка (1; 1) принадлежит и графику функции 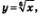 , и графику функции у=2-x. Значит, наше уравнение имеет один корень: х = 1 — абсцисса точки А. , и графику функции у=2-x. Значит, наше уравнение имеет один корень: х = 1 — абсцисса точки А.
Второй способ.
Геометрическая модель, представленная на рис. 173, наглядно иллюстрирует следующее утверждение, которое иногда позволяет очень изящно решить уравнение (и которым мы уже воспользовались в § 35 при решении примера 2):
Если функция у=f(х) возрастает, а функция у=g(х) убывает и если уравнение f(х)=g(х) имеет корень, то он только один.
Вот как, опираясь на это утверждение, мы можем решить заданное уравнение:
1) заметим, что при х = 1 выполняется равенство 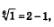 , значит, х = 1 — корень уравнения (этот корень мы угадали); , значит, х = 1 — корень уравнения (этот корень мы угадали);
2) функция y=2-x убывает, а функция 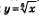 возрастает; значит, корень у заданного уравнения только один, и этим корнем является найденное выше значение x = 1. возрастает; значит, корень у заданного уравнения только один, и этим корнем является найденное выше значение x = 1.
Ответ: x = 1.
До сих пор мы говорили о функции 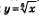 только для неотрицательных значений аргумента. Но ведь если п — нечетное число, выражение только для неотрицательных значений аргумента. Но ведь если п — нечетное число, выражение 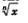 имеет смысл и для x <0. Значит, есть смысл поговорить о функции имеет смысл и для x <0. Значит, есть смысл поговорить о функции 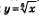 в случае нечетного п для любых значений х. в случае нечетного п для любых значений х.
Собственно говоря, к перечисленным добавится только одно свойство:
если n — нечетное число (n = 3,5, 7,...), то 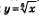 — нечетная функция. — нечетная функция.
В самом деле, пусть 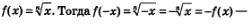 для нечетного показателя n такие преобразования верны. Итак, f(-x) = -f(x), а это и означает нечетность функции. для нечетного показателя n такие преобразования верны. Итак, f(-x) = -f(x), а это и означает нечетность функции.
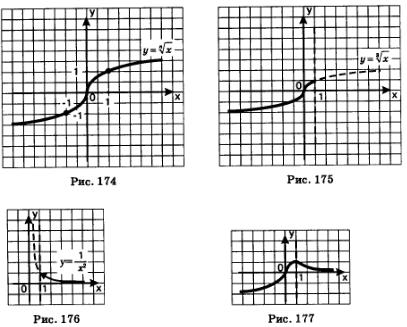
Как же выглядит график функции 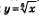 в случае нечетного показателя n? При в случае нечетного показателя n? При 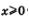 так, как показано на рис. 169, — это ветвь искомого графика. Добавив к ней ветвь, симметричную ей относительно начала координат (что, напомним, характерно для любой нечетной функции), получим график функции так, как показано на рис. 169, — это ветвь искомого графика. Добавив к ней ветвь, симметричную ей относительно начала координат (что, напомним, характерно для любой нечетной функции), получим график функции 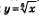 (рис. 174). Обратите внимание: ось у является касательной к графику в точке х = 0. (рис. 174). Обратите внимание: ось у является касательной к графику в точке х = 0.
Итак, повторим еще раз:
если п — четное число, то график функции 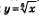 имеет вид, представленный на рис. 169; имеет вид, представленный на рис. 169;
если п — нечетное число, то график функции 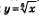 имеет вид, представленный на рис. 174. имеет вид, представленный на рис. 174.
Пример 3. Построить и прочитать график функции у = f(x), где 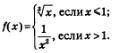
Решение. Сначала построим график функции 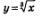 и выделим его часть на луче и выделим его часть на луче 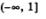 (рис. 175). (рис. 175).
Затем построим график функции 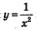 и выделим его часть на открытом луче и выделим его часть на открытом луче 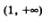 (рис. 176). Наконец, оба «кусочка» изобразим в одной системе координат — это и будет график функции у = f(x)(рис. 177). (рис. 176). Наконец, оба «кусочка» изобразим в одной системе координат — это и будет график функции у = f(x)(рис. 177).
Перечислим (опираясь на построенный график) свойства функции у = f(x):
1) 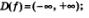
2) ни четна, ни нечетна;
3) убывает на луче 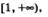 , возрастает на луче , возрастает на луче 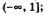
4) не ограничена снизу, ограничена сверху;
5) нет наименьшего значения, а 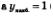 (достигается в точке х = 1); (достигается в точке х = 1);
6) непрерывна;
7) 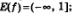
8) выпукла вниз при 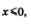 , выпукла вверх на отрезке [0, 1], выпукла вниз при , выпукла вверх на отрезке [0, 1], выпукла вниз при 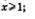
9) функция дифференцируема всюду, кроме точек х = 0 и х = 1.
10) график функции имеет горизонтальную асимптоту 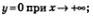 это означает, напомним, что это означает, напомним, что 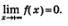
Пример 4. Найти область определения функции:
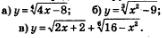
Решение, а) Под знаком корня четной степени должно находиться неотрицательное число, значит, задача сводится к решению неравенства 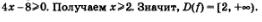
б) Под знаком корня нечетной степени может находиться любое число, значит, здесь на х не накладывается никаких ограничений, т.е. D(f) = R.
в) Выражение 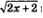 имеет смысл при условии имеет смысл при условии 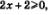 а выражение а выражение 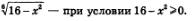 Значит, должны одновременно выполняться два неравенства: Значит, должны одновременно выполняться два неравенства: 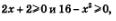 т.е. задача сводится к решению системы неравенств: т.е. задача сводится к решению системы неравенств:
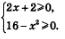
Решая неравенство 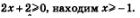
Решим неравенство 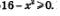 Разложим левую часть неравенства на множители: Разложим левую часть неравенства на множители: 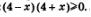 Левая часть неравенства обращается в 0 в точках -4 и 4. Отметим эти точки на числовой прямой (рис. 178). Числовая прямая разбивается указанными точками на три промежутка, причем на каждом промежутке выражение р(х)=(4-х)(4 + х) сохраняет постоянный знак (знаки указаны на рис. 178). Промежуток, на котором выполняется неравенство р(х)>0, заштрихован на рис. 178. По условию задачи нас интересуют и те точки х, в которых выполняется равенство р(х) = 0. Таких точек две: х =-4, х =4 — они отмечены на рис. 178 темными кружочками. Таким образом, на рис. 178 представлена геометрическая модель решения второго неравенства системы. Левая часть неравенства обращается в 0 в точках -4 и 4. Отметим эти точки на числовой прямой (рис. 178). Числовая прямая разбивается указанными точками на три промежутка, причем на каждом промежутке выражение р(х)=(4-х)(4 + х) сохраняет постоянный знак (знаки указаны на рис. 178). Промежуток, на котором выполняется неравенство р(х)>0, заштрихован на рис. 178. По условию задачи нас интересуют и те точки х, в которых выполняется равенство р(х) = 0. Таких точек две: х =-4, х =4 — они отмечены на рис. 178 темными кружочками. Таким образом, на рис. 178 представлена геометрическая модель решения второго неравенства системы.
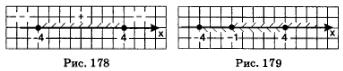
Отметим найденные решения первого и второго неравенств системы на одной координатной прямой, использовав для первого — верхнюю, а для второго — нижнюю штриховку (рис. 179). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Таким промежутком является отрезок [-1, 4].
Ответ. D(f) = [-1,4].
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|