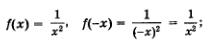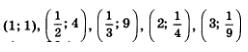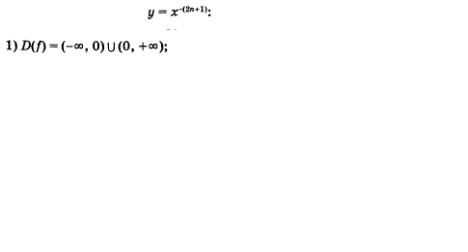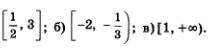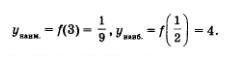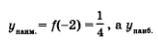|
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Функции у = x-n (n є N), их свойства и графики
Функции у = x-n (n є N), их свойства и графики
Продолжаем расширять класс функций, с которыми нам нужно, образно говоря, познакомиться накоротке. В предыдущем параграфе таковыми были степенные функции с натуральным показателем у=xn, а в этом параграфе мы рассмотрим функции вида у = x-n где n — натуральное число. Их называют степенными функциями с отрицательным целым показателем.
По определению степени с отрицательным показателем, 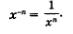
Поэтому вместо записи у = х-n можно использовать запись
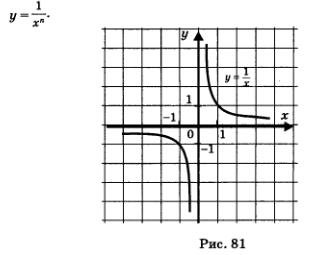
Одну функцию такого вида мы с вами изучили в курсе алгебры 8-го класса — это была функция 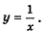 Вам известны и свойства этой функции, и ее график — гипербола (рис. 81). Сделаем следующий шаг: рассмотрим функцию Вам известны и свойства этой функции, и ее график — гипербола (рис. 81). Сделаем следующий шаг: рассмотрим функцию 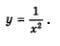 Начнем с исследования функции Начнем с исследования функции 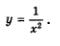 на четность, что, видимо, вас не удивит. Вспомните, ведь и в предыдущем параграфе мы начинали с использования четности функции у = х4 и нечетности функции у = х3. на четность, что, видимо, вас не удивит. Вспомните, ведь и в предыдущем параграфе мы начинали с использования четности функции у = х4 и нечетности функции у = х3.
Итак, докажем, что 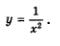 — четная функция. — четная функция.
Заметим прежде всего, что область определения функции — множество всех действительных чисел, за исключением значения х = 0; это — симметричное множество. Далее имеем: 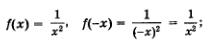
таким образом, для любого х из области определения функции выполняется равенство f(-х) = f(х). Это значит, что 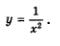 — четная функция. — четная функция.
Свойство четности функции 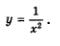 нам сейчас очень пригодится. Мы ведь знаем, что график четной функции симметричен относительно оси ординат. Значит, можно поступить так: рассмотреть эту функцию на открытом луче (0, ) и построить ее график на указанном луче. Затем, используя симметрию, построить график функции на всей числовой прямой и с его помощью перечислить свойства функции по той схеме, которая была использована в предыдущем параграфе. нам сейчас очень пригодится. Мы ведь знаем, что график четной функции симметричен относительно оси ординат. Значит, можно поступить так: рассмотреть эту функцию на открытом луче (0, ) и построить ее график на указанном луче. Затем, используя симметрию, построить график функции на всей числовой прямой и с его помощью перечислить свойства функции по той схеме, которая была использована в предыдущем параграфе.
1. Функция 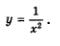 , x > О , x > О
Составим таблицу значений для этой функции:
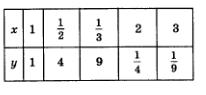
Построим точки 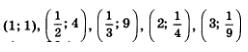 на координатной плоскости (рис. 82а), они намечают некоторую линию, проведем ее (рис. 826). на координатной плоскости (рис. 82а), они намечают некоторую линию, проведем ее (рис. 826).
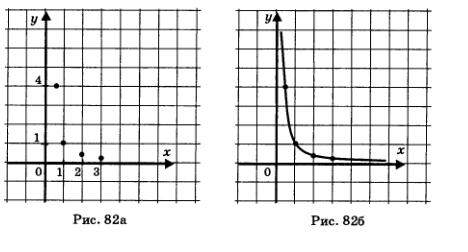
2. Функция у = x-2
Рассмотрим график, изображенный на рис. 826. Добавив к нему ветвь, симметричную построенной относительно оси ординат, получим график функции
Свойства функции у = х -2:
1 ) 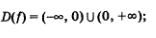
2) четная функция;
3) убывает на открытом луче (0, +оо), возрастает на открытом луче (-оо, 0);
4) ограничена снизу, не ограничена сверху;
5) нет ни наименьшего, ни наибольшего значений;
6) непрерывна при х < 0 (т.е. на открытом луче (-оо, 0)) и при х > 0 (т.е. на открытом луче (0, +оо));
7) Е(f) = (0,+оо);
8) выпукла вниз и при х < 0, и при х > 0.
Как и в предыдущем параграфе, свойства 1) - 5) мы в состоянии доказать строго. Докажем для примера убывание функции при х > 0. Пусть х1> х2> 0. По свойствам числовых неравенств, имеем:
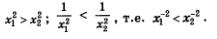 Итак, для функции у = f(х), где f(х) = х-2, мы доказали, что из х1 > х2 > 0 следует f(х2) < f(х2), а это и означает убывание функции на открытом луче (0, +оо). Итак, для функции у = f(х), где f(х) = х-2, мы доказали, что из х1 > х2 > 0 следует f(х2) < f(х2), а это и означает убывание функции на открытом луче (0, +оо).
3. Функция у = х-2n
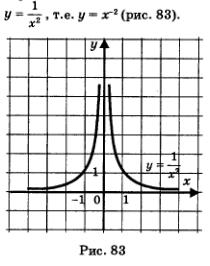
Речь идет о функциях 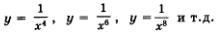 График любой такой функции похож на график функции График любой такой функции похож на график функции 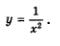 (рис. 83). Отметим, что кривая (рис. 83). Отметим, что кривая 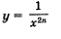 асимптотически приближается к осям координат. Говорят также, что ось х (т.е. прямая у = 0) является горизонтальной асимптотой графика функции асимптотически приближается к осям координат. Говорят также, что ось х (т.е. прямая у = 0) является горизонтальной асимптотой графика функции 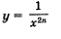 , а ось у (т.е. прямая х = 0) является вертикальной асимптотой этого графика. , а ось у (т.е. прямая х = 0) является вертикальной асимптотой этого графика.
4. Функция у = x-(2n+1)
Речь идет о функциях 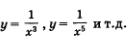 График любой такой функции похож на график функции График любой такой функции похож на график функции 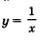 (рис. 81). (рис. 81).
Отметим, что ось х является горизонтальной асимптотой графика функции 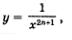 а ось у является вертикальной асимптотой этого графика. а ось у является вертикальной асимптотой этого графика.
Свойства функции
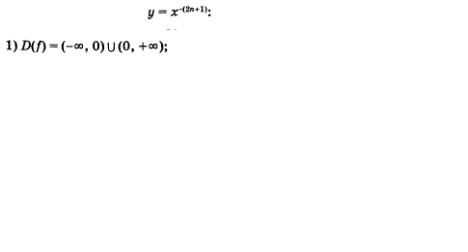
2) нечетная функция;
3) убывает на открытом луче (0, +оо) и на открытом луче (+оо,0);
4) не ограничена ни снизу, ни сверху;
5) нет ни наименьшего, ни наибольшего значений;
6) непрерывна при х < 0 и при х > 0;
7) Е(f) = (+оо,0) U (0, +оо);
8) выпукла вверх при х < 0, выпукла вниз при х > 0.
Пример 1.
Найти наименьшее и наибольшее значения функции 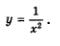 на заданном промежутке: на заданном промежутке:
а) 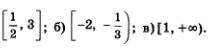
Решение.
Для ответа на поставленный вопрос можно использовать график функции (рис. 83), а можно опираться на свойство монотонности; ниже мы будем действовать и так, и так.
а)Функция убывает при х > 0, значит, свое наименьшее и наибольшее значения она может достигать только на концах промежутка (соответственно, на правом и левом), если, разумеется, эти концы принадлежат промежутку. В рассматриваемом случае
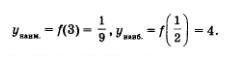
б) Функция возрастает при х < 0, значит, свое наименьшее и наибольшее значения она может достигать только на концах промежутка (соответственно на левом и правом), если, разумеется, эти концы принадлежат промежутку. В рассматриваемом случае 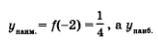 не существует (правый конец не принадлежит заданному промежутку). не существует (правый конец не принадлежит заданному промежутку).
в) С помощью графика функции (рис. 83) устанавливаем, что 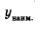 не существует, а не существует, а 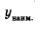 = 1. = 1.
Пример 2.
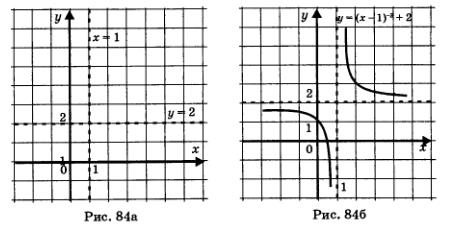
Построить график функции у = (х- I)-3 + 2.
Решение.
1) Перейдем к вспомогательной системе координат с началом в точке (1; 2) (пунктирные прямые x= 1 и у = 2 на рис. 84а).
2) Привяжем функцию у = х-3 к новой системе координат — это и будет требуемый график (рис. 846).
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|