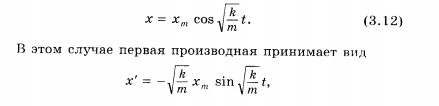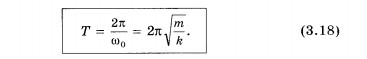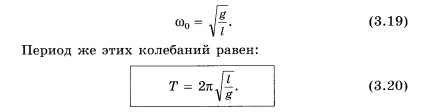|
Гипермаркет знаний>>Физика и астрономия>>Физика 11 класс>> Гармонические колебания
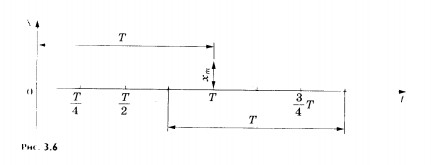
§ 22 ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Ускорение — вторая производная координаты по времени. Мгновенная скорость точки, как вам известно из курса математики, представляет собой производную координаты точки по времени. Ускорение точки — это производная ее скорости по времени, или вторая производная координаты по времени. Поэтому уравнение (3.4) можно записать так: Гармонические колебания. Из курса математики известно, что вторые производные синуса и косинуса по их аргументу пропорциональны самим функциям, взятым с противоположным знаком. В математическом анализе доказывается, что никакие другие функции таким свойством не обладают. Все это позволяет с полным основанием утверждать, что координата тела, совершающего свободные колебания, меняется с течением времени по закону синуса или пасинуса. На рисунке 3.6 показано изменение координаты точки со временем по закону косинуса.
Амплитуда колебаний. Амплитудой гармонических колебаний называется модуль наибольшего смещения тела от положения равновесия. Амплитуда может иметь различные значения в зависимости от того, насколько мы смещаем тело от положения равновесия в начальный момент времени, или от того, какая скорость сообщается телу. Амплитуда определяется начальными условиями, а точнее энергией, сообщаемой телу. Но максимальные значения модуля синуса и модуля косинуса равны единице. Поэтому решение уравнения (3.11) не может выражаться просто синусом или косинусом. Оно должно иметь вид произведения амплитуды колебаний хm на синус или косинус. Решение уравнения, описывающего свободные колебания. Запишем решение уравнения (3.11) в следующем виде:
Период и частота гармонических колебаний. При колебаниях движения тела периодически повторяются. Промежуток времени Т, за который система совершает один полный цикл колебаний, называется периодом колебаний. Зная период, можно определить частоту колебаний, т. е. число колебаний в единицу времени, например за секунду. Если одно колебание совершается за время Т, то число колебаний за секунду Частоту свободных колебаний нааынают собственной частотой колебательной системы1. Зависимость частоты и периода свободных колебаний от свойств системы. Собственная частота колебаний тела, прикрепленного к пружине, согласно уравнению (3.13) равна: Замечательно, что период колебаний тела на пружине и период колебаний маятника при малых углах отклонения не зависят от амплитуды колебаний. Модуль коэффициента пропорциональности между ускорением Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебаний, можно очень точно определить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно не везде одинаково. Ведь плотность земной коры не всюду одинакова. В районах, где залегают плотные породы, ускорение g несколько большее. Это учитывают при поисках полезных ископаемых. Так, железная руда обладает повышенной плотностью по сравнению с обычными породами. Проведенные под руководством академика А. А. Михайлова измерения ускорения свободного падения под Курском позволили уточнить места залегания железной руды. Сначала они были обнаружены посредством магнитных измерений. Свойства механических колебаний используются в устройствах большинства электронных весов. Взвешиваемое тело кладут на платформу, под которой установлена жесткая пружина. В результате возникают механические колебания, частота которых измеряется соответствующим датчиком. Микропроцессор, связанный с этим датчиком, переводит частоту колебаний в массу взвешиваемого тела, так как эта частота зависит от массы. Полученные формулы (3.18) и (3.20) для периода колебаний свидетельствуют о том, что период гармонических колебаний зависит от параметров системы (жесткости пружины, длины нити и т. д.)
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: